2025 AIChE Annual Meeting

(260b) Quantum Optimization Benchmark Library

Authors

Pedro Maciel Xavier, Purdue University
Optimization is the methodological backbone behind the operations of major industrial areas, including Logistics, Manufacturing, Power Systems, and Process Systems Engineering (PSE) [1], to name a few. In the face of many challenging Combinatorial Optimization problems, the development of novel specialized hardware has been an active research area over the past decade, which has led to fundamental advancements in Quantum Computing and other Physics-inspired devices and algorithms [2]. Optimization is a well-established domain in quantum applications research on existing and near-term quantum hardware [3]. The field is driven by heuristic quantum algorithms compatible with the hardware, such as the Quantum Approximate Optimization Algorithm, or QAOA [4]. Recent hardware improvements pave the way for thorough benchmarking of heuristic quantum algorithms at scale [5].

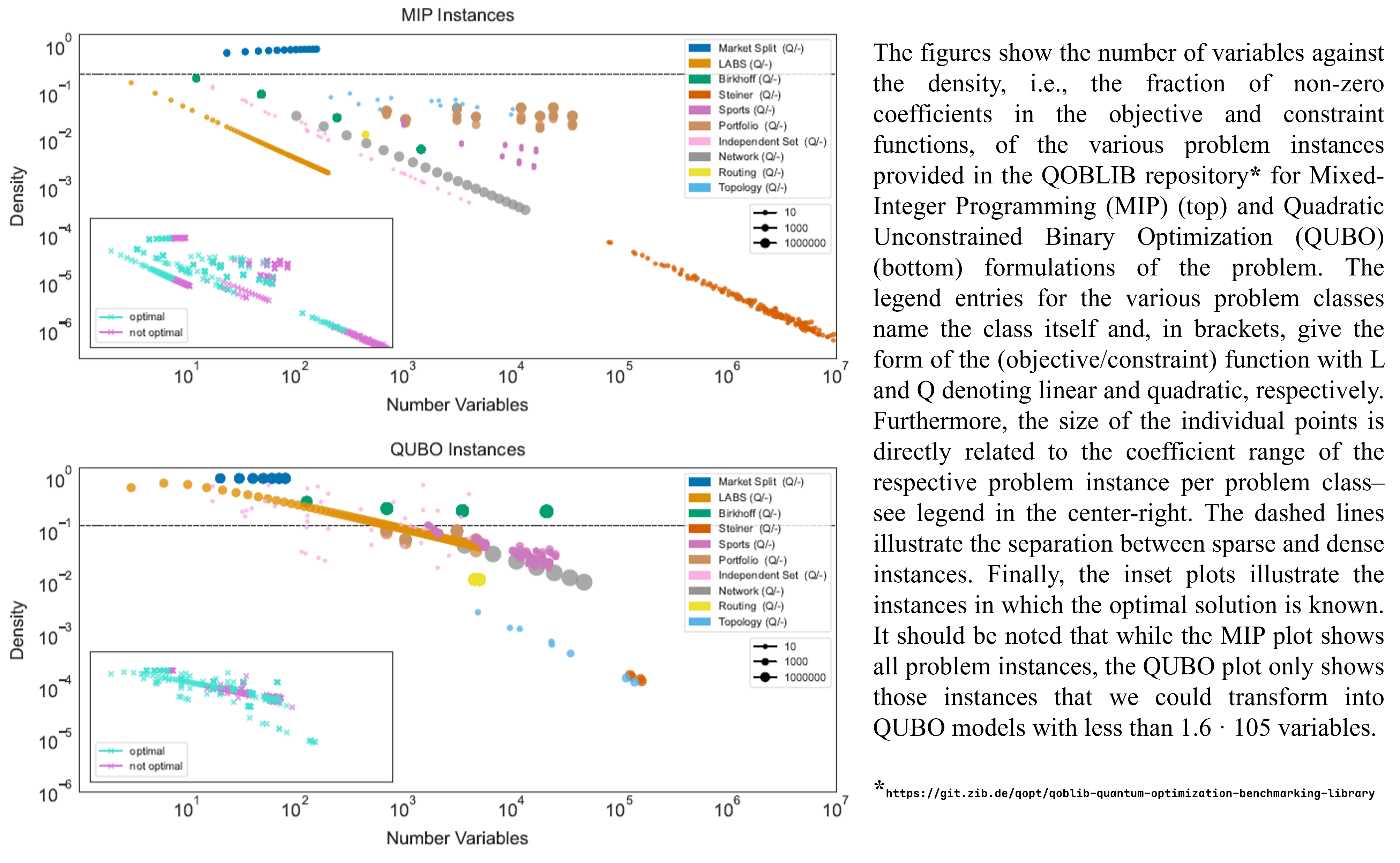
This work presents ten optimization problem classes that are difficult for existing classical algorithms and can be linked to practically relevant applications, aiming to enable a fair, comparable, and meaningful benchmarking effort for quantum optimization methods. The initial compilation contains instances of the problems known as Market Split; Low Autocorrelation Binary Sequences; Minimum Birkhoff Decomposition; Steiner Tree Packing; Sports Tournament Scheduling; Portfolio Optimization; Independent Set; Network Design; Vehicle Routing Problem; and Topology Design. These are primarily typical Combinatorial Optimization problems best known through their Mixed-Integer Programming (MIP) formulations, which were then cast into a corresponding QUBO formulation [6].

While these problem classes vary in their individual properties, like objective and variable type, coefficient ranges, and density, they all become challenging for established classical methods at system sizes of about 100 to 10,000 decision variables. The small sizes at which difficult problem instances appear enable testing quantum algorithms for these problems already today. This is not, however, a static collection, and the archive is expected to grow over time with contributions. We envision the PSE and the Chemical Engineering community in general being able to provide this database with interesting and relevant instances, as it did in the composition of the Library of Mixed-Integer and Continuous Nonlinear Programming Instances (MINLPLib) [7].

In this work, we reference the results from state-of-the-art solvers for instances from all problem classes and demonstrate exemplary baseline results obtained with quantum solvers for selected classes. The baseline results illustrate our suggested benchmark reporting, aiming for comparability of the used methods, reproducibility of the respective solutions, and trackability of algorithmic and hardware improvements. We encourage the optimization community to explore the performance evaluation of available classical or quantum algorithms and hardware with the benchmarking problem instances presented in this library.

This work was an effort of the IBM Quantum Optimization Working Group and resulted in the paper “Quantum Optimization Benchmark Library The Intractable Decathlon”, already submitted to ArXiV, but still on the way to publication; and the Quantum Optimization Benchmark Library (QOBLIB) repository [8].

References
[1] https://aiche.onlinelibrary.wiley.com/doi/full/10.1002/aic.17651
[2] https://arxiv.org/abs/2310.03011
[3] https://www.nature.com/articles/s42254-024-00770-9
[4] https://arxiv.org/abs/1709.03489
[5] https://arxiv.org/pdf/2502.06471
[6] https://arxiv.org/abs/2307.02577
[7] https://www.minlplib.org/index.html
[8] https://git.zib.de/qopt/qoblib-quantum-optimization-benchmarking-library