2025 AIChE Annual Meeting
(12b) Optimal Well Design and Injection Planning for CO2 Storage into Deep Saline Aquifers Using Mathematical Programming
Authors
Numerous studies have shown that injection strategies deeply influence the extension of the CO2 front (usually called “plume”), thereby affecting brine displacement and overall storage efficiency [Kumar, 2007; Shamshiri & Jafarpour, 2010]. However, accurately predicting plume extension requires solving highly nonlinear and nonconvex systems of coupled partial differential equations. As a result, simulation-based optimization (SBO) has become the predominant approach in literature [Zou & Durlofsky, 2023]. SBO typically combines high-fidelity numerical reservoir simulators (NRS) with heuristic or sampling-based algorithms aimed at identifying injection plans that improve the so-called fitness function. Nevertheless, such methods face several limitations. On the one hand, simulators often operate as proprietary “black-box” systems, precluding access to internal derivatives and thereby restricting the use of gradient-based optimization techniques. On the other hand, SBO relies on heuristic search methods that entail a large number of simulations (in the order of hundreds or even thousands), rendering the process computationally expensive, without reference to the quality of the solution.
To overcome these challenges, the research team has recently proposed a physics-informed optimization approach based on mathematical programming, devised for 2D representations of the reservoir [Trucco et al., 2025]. In that model, first-principle equations—such as Darcy’s law—are embedded directly into a Nonlinear Programming (NLP) formulation, using a spatial-time discretization. The framework leverages the use of derivative information through advanced reduced-gradient solvers, yielding enhanced convergence properties and low computational costs. Furthermore, subsurface engineering constraints and regulatory requirements can be explicitly incorporated into the formulation as constraints, without the need for penalization terms and feasibility repair procedures that often deteriorate the solution quality. Prior results have demonstrated the ability of the NLP model to achieve local optimal solutions more efficiently than metaheuristics for this problem.
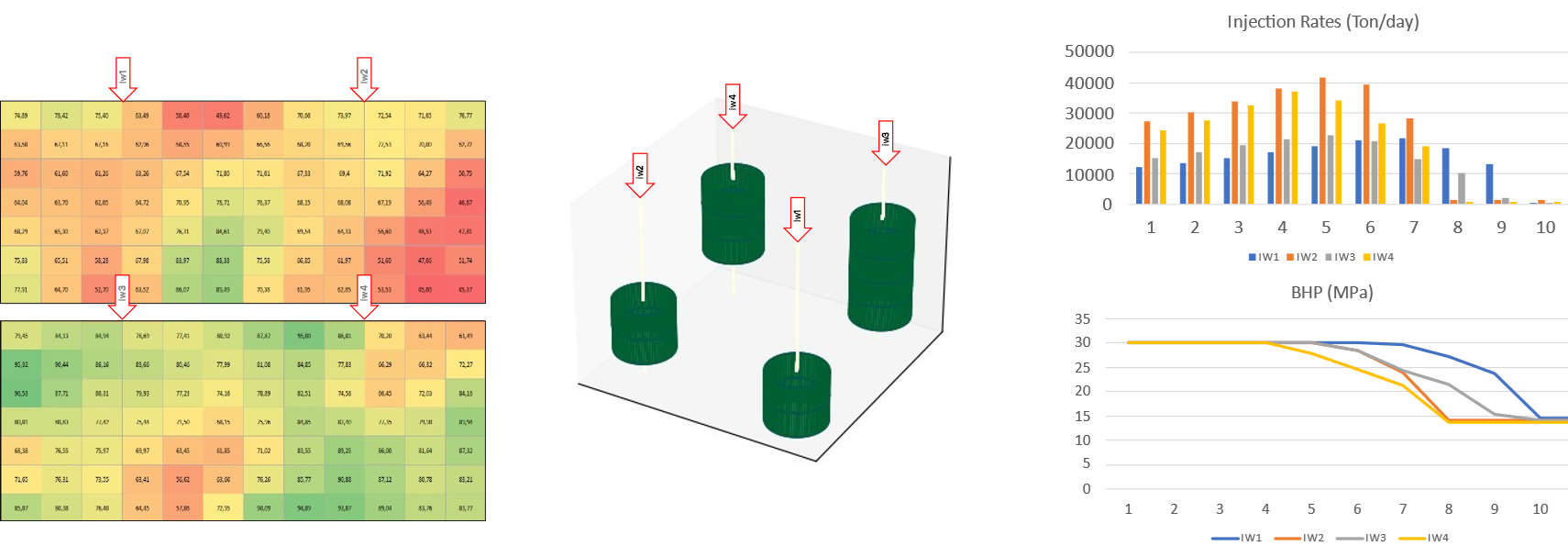
Building upon these findings, the current work extends the model’s capabilities in two principal directions. First, the model transitions from a 2D to a 3D coordinate system to better approximate the physical characteristics of real-world reservoirs. The novel 3D representation is based on a cylindrical abstraction that reflects the radial nature of pressure propagation and CO2 plume migration around vertical injection wells, thus providing an accurate tool to manage storage capacity. The modified discretization is made up of cells with non-uniform sizes, whose geophysical properties (namely permeability and porosity) may also vary in space. Second, the optimization framework is enhanced by including discrete decisions concerning the depth of injection points along each vertical well. Motivated by previous results suggesting that the injection layers significantly affect storage efficiency [Trucco et al., 2025], the new model introduces 0-1 variables to represent the geological layers selected for injection. This extension yields a Mixed-Integer Nonlinear Programming (MINLP) formulation that can find more efficient solutions, taking advantage of heterogeneous properties across the reservoir while mitigating pressure interference among adjacent wells.
Summarizing, the extended optimization problem addressed in this work can be formally stated as follows. Given are: (a) a multi-layer, heterogeneous saline aquifer with known geological properties in 3D; (b) a set of vertical injection wells with predetermined placement in the x-y coordinates of the aquifer; (c) a long-term, multi-period planning horizon; and (d) a maximum amount of CO2 available for injection at every period to be distributed among the wells. The objective is to determine the optimal design for each well (injection layers), the bottom-hole pressure and injection rates over time, so as to maximize the cumulative amount of CO2 stored by the end of the planning horizon. The problem is limited by two primary operational constraints: (i) maintaining pressure at each block below critical fracture thresholds, and (ii) ensuring that the CO2 plume remains contained within a prescribed control volume to avoid leakage risks in the long term.
The transition from a continuous NLP to an MINLP formulation introduces significant computational challenges. In the original 2D model, active-set solvers such as CONOPT [Drud, 1996] have demonstrated superior performance as they navigate the feasible region along constraint boundaries. These solvers are particularly effective in preserving feasibility once it is achieved, which is essential given the stringent requirement to satisfy thousands of mass and pressure balance constraints across the discretized reservoir domain. However, typical MINLP solvers such as branch-and-bound often disrupt this feasibility. In particular, each branching decision involves fixing a binary variable to either zero or one, which can render previous solutions infeasible, yielding a very large number of iterations to solve each child node. To overcome this, a tailored solution algorithm has been developed. The algorithm begins by solving the relaxed MINLP model and afterwards enforcing the integrality condition of 0-1 variables by means of penalty terms in the objective function. An iterative procedure makes 0-1 variables be gradually driven toward one of their integer bounds. By maintaining feasibility of mass and pressure balances throughout the optimization process, the algorithm mitigates instability commonly observed in pressure-sensitive reservoir models and enhances convergence toward high-quality, physically consistent solutions.
Several instances of an illustrative case study have been conducted to evaluate the performance of the proposed MINLP model under realistic conditions. Each scenario considers a reservoir discretized into four directions, with 84 blocks per direction and seven geological layers, resulting in a total of 336 volume elements. Four injection wells are positioned in a rectangular configuration, and each well can be opened up to any of the vertical layers. The planning horizon spans over 20 years: CO2 injection is allowed during the first 9 years, followed by an additional 11-years containment period in which the plume must remain within prescribed boundaries to ensure long-term storage.
The resulting optimization model comprises 245,417 decision variables and 266,477 constraints. The model has been solved using CONOPT4, requiring approximately four hours of CPU time per instance to converge to an optimal solution. It is worth highlighting that a substantial portion of the computational time is spent by the initial iteration, during which the solver seeks to establish a feasible point that satisfies the full set of mass and pressure balance equations across the reservoir domain. This observation reinforces the importance of preserving feasibility throughout the optimization process and underscores the limitations of typical MINLP solution strategies.
Results demonstrate that the optimal selection of injection layers plays a pivotal role in enhancing storage performance, particularly in the presence of geological heterogeneity. In contrast to uniform reservoir instances, heterogeneous permeability distributions yield better solutions and also guide the optimization process toward more efficient outcomes by breaking symmetries, thereby accelerating convergence. In general, the model tends to favor deeper injections into multiple layers; however, it is not optimal for all wells to target the same layers, as pressure interference between wells becomes a limiting factor and must be carefully managed.
Overall, this work extends the capabilities of former mathematical models for optimizing CO2 injection into deep saline aquifers. It reinforces the value of mathematical programming in supporting strategic decisions for well design and injection planning with the aim of maximizing storage efficiency. However, it is important to emphasize that optimization models do not replace high-fidelity reservoir simulation. The solutions identified through these models must still be validated using detailed numerical simulators. Nevertheless, compared to metaheuristics that typically require numerous simulations, mathematical programming approaches significantly reduce the number of validation steps, as they converge more directly toward promising configurations. Future work will focus on extending the current framework to include other physical features like compressibility, miscibility and thermodynamic phenomena, thus leveraging its applicability to large-scale, real-world CCS projects.
References
[1] Air Products and Chemicals Inc., 2025. Louisiana Clean Energy Complex. https://www.airproducts.com/energy-transition/louisiana-clean-energy-co… (accessed 19 March 2025).
[2] Drud, A.S., 1996. CONOPT—a large-scale GRG code. ORSA J. Comput. 6 (2), 207–216.
[3] Ismail, I., Gaganis, V., 2023. Carbon capture, utilization, and storage in saline aquifers: Subsurface policies, development plans, well control strategies and optimization approaches—A review. Clean Technol. 5 (2), 609–637.
[4] Kumar, D., 2007. Optimization of well settings to maximize residually trapped CO2 in geologic carbon sequestration. Master’s Thesis, Stanford University, Stanford, CA.
[5] Shamshiri, H., Jafarpour, B., 2010, November. Optimization of geologic CO2 storage in heterogeneous aquifers through improved sweep efficiency. In: SPE Int. Conf. on CO2 Capture, Storage, and Utilization, pp. SPE-139643. SPE.
[6] Trucco, D., Presser, D., Cafaro, D., Grossmann, I., Shenvi Usgaonkar, S., Zhang, Q., Misra, P., Binagia, H., Rowe, W., Mehta, S., 2025. A Mathematical Programming Model for the Optimal Utilization of Deep Saline Aquifers for CO2 Storage. Submitted for publication to Comput Chem Eng.
[7] Zou, A., Durlofsky, L.J., 2023. Integrated framework for constrained optimization of horizontal/deviated well placement and control for geological CO2 storage. SPE J. 28, 2462–2481.