2025 AIChE Annual Meeting
(12a) Computationally Efficient Framework for the Optimal Design of Large-Scale Pipeline Networks with General Topologies and Multiphase Flows
Authors
Pipeline network optimization is further complicated by the time-varying nature of well production profiles, particularly in unconventional reservoirs where production typically exhibits an initial peak followed by a steep decline. Moreover, the implementation of enhanced production techniques, such as refracturing, artificial lifting or waterflooding, can lead to erratic flowrates and compositions over the asset’s lifecycle. At its core, this problem can be framed as a multiperiod allocation problem, similar to the bin-packing problem [Montagna et al., 2021; Presser et al., 2024], wherein production from different wells must be allocated to processing facilities of different capacities. However, two primary factors contribute significantly to its complexity. First, the underlying network topology introduces a combinatorial explosion of feasible configurations, especially when alternative pipeline diameters and facility locations are considered. Second, the nonlinear and non-convex nature of multiphase hydraulic equations must be accurately captured to ensure feasibility of the network design.
To overcome these challenges, this work proposes a generalized mathematical optimization framework capable of solving large-scale instances of the multiphase gathering network design problem under realistic operational conditions. In contrast to previous contributions [Presser et al., 2025] the framework is agnostic to the hydraulic model and/or correlation used to predict multiphase fluid dynamics, thereby allowing different approaches as required by the decision-maker. Furthermore, no limiting assumptions are imposed on the network topology.
The optimization problem is formally defined as follows. Given are: (a) a long-term, multiperiod planning horizon, (b) a set of production wells with forecasted productivity profiles and wellhead pressures; (c) a set of candidate facility locations, associated processing capacities, capital expenditures, and operating costs; (d) a set of feasible pipeline connections between nodes, available pipeline diameters, installation and operating costs; and (e) minimum pressure requirements at processing nodes. The objective is to determine the optimal number, location, and size of processing facilities, as well as the topology and diameter of pipeline segments across the gathering network, such that the total net present cost is minimized. Fluid-dynamic conditions are ensured by imposing that every multiphase stream maintains sufficient pressure throughout its assigned path.
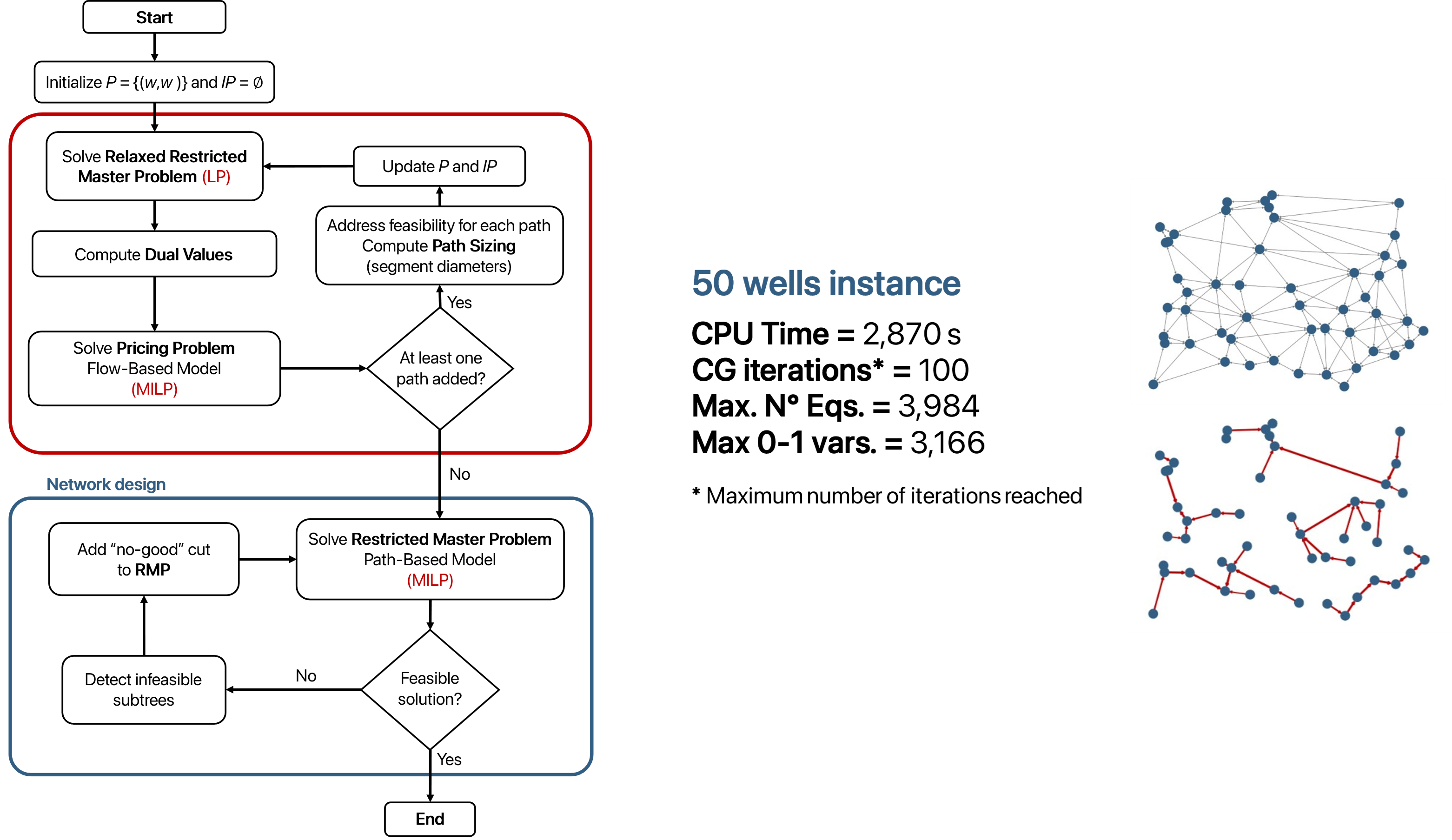
The proposed solution approach is decomposed into two algorithmic methods, each tailored to address one of the intrinsic sources of complexity. On the one hand, efforts are focused on progressively adding complicating constraints, drawing inspiration from the Selective Tightening Algorithm (STA) [Presser et al., 2024]. STA adopts a row-generation strategy wherein critical hydraulic constraints on promising arcs are iteratively incorporated into the model. Unlike the traditional STA approach, the methodology proposed in this work avoids the explicit inclusion of highly nonlinear fluid-dynamic constraints. Instead, infeasible configurations identified through offline hydraulic evaluations are excluded via integer cuts. This allows the optimization model to remain within the class of mixed-integer linear programming (MILP), enabling efficient solution procedures. One of the keys of the algorithm is the identification of Minimal Infeasible Trees, defined as the smallest network substructure whose selection leads to infeasibility. By excluding these subgraphs, the algorithm can effectively prune large portions of the solution space without requiring exhaustive enumeration.
Despite the aforementioned advancement, scalability remains a significant challenge. The number of integer cuts required to achieve a feasible solution increases rapidly with the size of the network, leading to intractability for instances beyond 20 nodes. So far, the problem has been formulated using a flow-based framework, where each potential connection may be selected unless explicitly excluded by an integer cut. This approach guarantees global optimality, but the computational burden becomes prohibitive as network size increases. To overcome this limitation, the problem is reformulated using a path-based modeling approach. In this context, a path is defined as a sequence of arcs through which production from a given well can reach a processing facility. Consequently, the pipeline network can be interpreted as a combination of paths, one for each producing node. The decision variables in the new formulation are no longer associated with individual connections but rather with entire paths. Needless to say, the number of paths grows exponentially with the network size, making full enumeration impractical. However, many of these paths can be readily identified as infeasible or suboptimal, and then be disregarded during the solution process. To this end, a second algorithmic component is developed based on column generation principles [Desaulniers et al., 2005] yielding a reduced subset of paths, hereafter referred to as columns.
In the path-based formulation, a relaxed restricted master problem (rRMP) is solved iteratively, with additional columns being incorporated by solving a pricing subproblem. The latter is modelled as a flow-based MILP formulation that enables the systematic detection of promising topological structures from dual values of the rRMP. The proposed framework initiates the optimization process from a fully decentralized configuration, in which a processing facility is installed at every production node. Iterations proceed until the pricing subproblem can no longer suggest more promising columns. At this point, the algorithm finally solves the restricted master problem (RMP) formulated as an MILP, building the network from the pool of paths.
It is important to emphasize that while individual paths are evaluated independently and confirmed to be hydraulically feasible during the column generation phase, their combination may result in conflicts when paths share some arcs (i.e., overlap). From that, integer cuts are still essential to enforce feasibility. However, candidate paths are pre-screened for feasibility and selected based on their cost-efficiency, reducing the search space and leading to high computational efficiency.
To assess the performance and scalability of the proposed framework, two computational experiments have been conducted. The first experiment seeks to evaluate both the solution quality and the computational efficiency of the algorithm. To this end, the framework is tested on 100 randomly generated instances comprising eight nodes. These instances are tractable using the conventional flow-based formulation, which serves as a benchmark for global optimal solutions. Results indicate that the proposed framework achieves a two-orders-of-magnitude reduction in computational time on average, at the expense of a mean relative deviation of 0.96% from the optimal cost. Moreover, 27 out of the 100 instances are solved to global optimality. These outcomes demonstrate that, for small instances, the algorithm is computationally efficient and also maintains a high level of accuracy when compared to exact methods.
In the second experiment, the framework is applied to larger problems consisting of 16, 32, and 50 nodes, which cannot be solved in reasonable times using the flow-based model. In all cases, the proposed method successfully produces good feasible solutions in less than one hour of computation. For the largest networks, the number of column generation steps needs to be limited to reduce the computational burden. Despite this restriction, the framework maintains its ability to find cost-effective designs.
Summarizing, the novel approach demonstrates the ability to obtain near-optimal solutions when benchmarked against exact methods in small-scale instances, and it remains computationally tractable for medium and large-scale networks where traditional methods fail to converge due to combinatorial complexity. Future work will focus on extending the framework to networks comprising more than 100 production nodes, including decisions regarding capacity expansion planning and single-component delivery after separation.
References
[1] Cafaro, D.C., Presser, D.J. & Grossmann, I.E. Recent contributions to the optimal design of pipeline networks in the energy industry using mathematical programming. TOP 30, 618–648 (2022). https://doi.org/10.1007/s11750-022-00635-3
[2] Desaulniers, G., Desrosiers, J. & Solomon, M.M. (eds). Column Generation. Springer, Boston, MA (2006). https://doi.org/10.1007/b135457
[3] Montagna, A.F., Cafaro, D.C., Grossmann, I.E. et al. Pipeline network design for gathering unconventional oil and gas production using mathematical optimization. Optim Eng 24, 539–589 (2023). https://doi.org/10.1007/s11081-021-09695-z
[4] Presser, D.J., Cafaro, D.C., Grossmann, I.E. et al. Selective tightening algorithm for the optimization of pipeline network designs in the energy industry. Comput Chem Eng 182, 108537 (2024). https://doi.org/10.1016/j.compchemeng.2023.108537
[5] Presser, D.J., Trucco, D.J., Cafaro, D.C., Grossmann, I.E. et al. Addressing multiphase fluid-dynamics in the optimal design of oil and gas pipeline networks. Manuscript in preparation for submission to Ind Eng Chem Res.