(639c) Mathematical Modeling of Cooperative Molecular Beacons to Design and Tune for Robust, Switch-like Detection

Introduction:

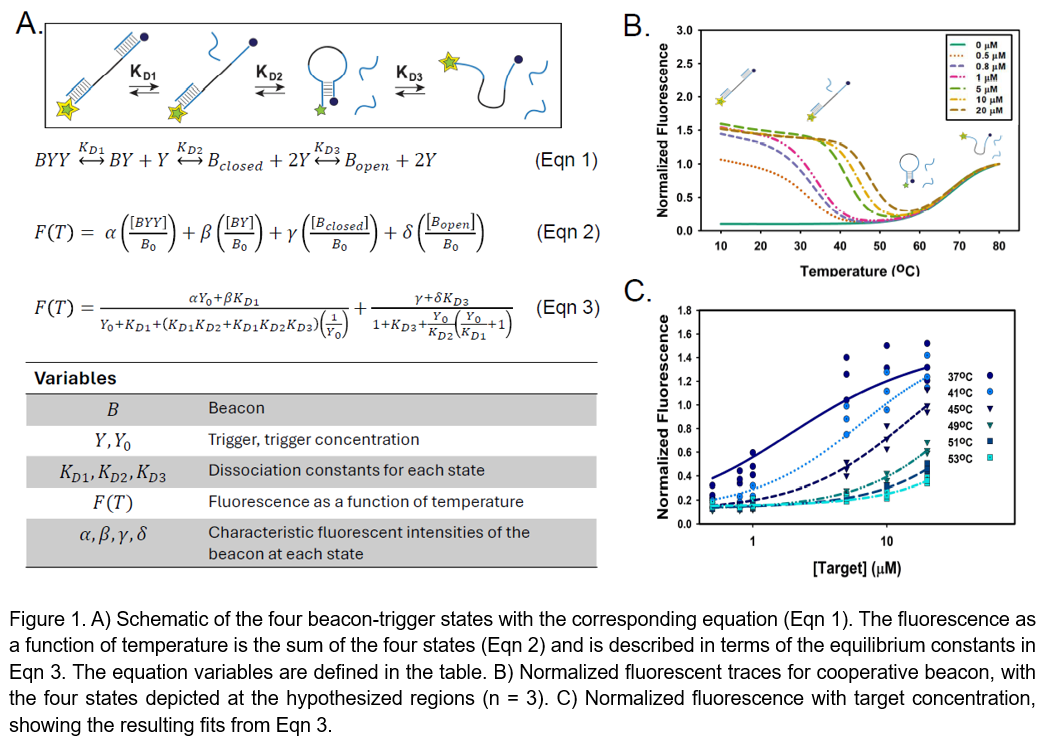
Molecular beacons offer a versatile platform to observe the binding behavior of oligonucleotides. These stem-loop DNA probes are modified with a fluorescent tag on one end and a quencher molecule on the other end. Binding at the stem brings the fluorophore and quencher into proximity and the fluorescence output is subdued due to Fluorescence Resonance Emission Transmission (FRET). When the beacon opens, the fluorophore and quencher are more distanced from each other, and the fluorescence increases. Beacon opening can be facilitated through melting, as high temperatures break the hydrogen bonding between the nucleic acid pairs, or by binding to a complementary target oligonucleotide. Conventional beacons contain a single target-binding site located inside the loop. The beacon can therefore exist in three general states: closed beacon (hairpin), open beacon (random coil), and beacon bound to the target. Modifications of the conventional beacon have included varying the stem length, placing the target binding site in both the stem and the loop, and adding a second target binding site within the loop. A second binding site creates the potential for a cooperative interaction. Cooperativity is a natural regulatory strategy by which a receptor is tuned to a higher or lower affinity for a target through subsequent binding events. Positive cooperativity is specifically when the receptor has a higher affinity, and the result is a steeper, switch-like response to a target as the receptor moves from an unbound state to a bound state. We hypothesize that positively cooperative DNA receptors can be fine-tuned through multiple target binding sites, creating a unique thermodynamic and kinetic profile for hybridization reactions and a distinct response outcome. To facilitate the design of cooperative DNA receptors, we have developed a new mathematical framework for analyzing and tuning the thermodynamic parameters of molecular beacons with two target binding sites. Our model adds a fourth state: beacon bound to two targets (Figure 1A, Eqn 1). Therefore, the fluorescence of a two-site molecular beacon is the sum of the four states (Figure 1A, Eqn 2), and an equation for the fluorescence in terms of the dissociation constants can be derived (Figure 1A, Eqn 3). For our cooperative beacon, we designed a DNA template with two identical binding sites that overlap within the stem of the beacon (Figure 1A). The beacon has a 4-nucleotide toehold on the 5’ end, which facilitates the first binding event to open the loop. The second binding site should then be more accessible for a second target, creating a switch-like response through a positively cooperative interaction.

Methods:

To assess the cooperativity of this design, the beacon was mixed with various concentrations of target and heated to measure fluorescence as a function of temperature. Six different concentrations of the target were mixed in a reaction buffer containing 1x Thermopol buffer (NEB), 4.004mM MgSO4 (NEB), 25mM Tris-HCl pH 8, 50mM KCl, 0.1 mg/mL BSA, and 200nM DNA beacon to a final volume of 20 µL. Triplicates of each sample were placed into a Bio-Rad CFX Connect thermocycler to collect real-time fluorescence readings. The samples were first cooled from 80°C to 10°C at a rate of -10 minutes/°C, then heated from 10°C to 80°C at a rate of 10 minutes/°C. This served the dual purpose of checking for hysteresis and annealing the targets to the beacon at 10°C. Therefore, the fluorescence data from the secondary melting stage (10°C to 80°C) was taken for analysis as we assume that the beacons are bound to target at the start of this temperature increase. Experiments were repeated with a quencher-less beacon molecule to measure the temperature dependence of the FAM fluorescence. Raw fluorescence traces were first baselined to the no-template controls, corrected for the FAM temperature dependence, and then normalized to one at 80°C. The normalized data was then fit to Equation 3 (Figure 1A) to calculate the dissociation constants at each temperature.

Results/Discussion:

The beacon in solution with the target initially had a high fluorescence at 10°C, which aligns with the assumption that the beacon is in an open state bound to the target (Figure 1B). As the temperature increased, the fluorescence dropped as the target melted off the beacon. The predicted target-beacon melting temperature was 42.4°C (UNAFold Web Server, DINAmelt). In this range between the target-beacon melting temperature and the beacon melting temperature, the beacon was in a closed state and the fluorescence was quenched. Above 60°C, the fluorescence increased again as the beacon entered the random coil state. This corresponds with the predicted beacon melting temperature of 64.6°C (UNAFold Web Server, DINAmelt). The fluorescence is dependent on the concentration of the target, despite an excess of target between 2.5-100 times the concentration of the beacon. This is due in part to the opportunity for two targets to bind to the beacon, and therefore the excess is only 1.25-50 times. This is most noticeable at the lowest target concentration of 0.5 µM, where the normalized fluorescence at 10°C is lower than the other five target concentrations. The temperature range for fitting the normalized fluorescence to Equation 3 was 37-55°C to capture the target concentration dependence (Figure 1C). Surprisingly, the calculated dissociation constants revealed an opposite effect than hypothesized. K_D1 was greater than K_D2 for temperatures below 52°C, indicating a negative cooperativity where the beacon had a reduced affinity for a second target. To elucidate this result further, we have designed beacons with two different binding sites but with similar predicted binding thermodynamics to our original identical-site beacon. These new beacons will be used to measure the dissociation constants experimentally, and this data will provide more information to assess the validity of our mathematical model.

Conclusion: We have developed a mathematical model to analyze cooperative DNA receptors using a molecular beacon platform. Importantly, this model distinguishes between the fluorescence of the beacon bound to targets versus in a random coil state. Further work is needed to validate and universalize this method for tuning cooperative receptors, but it lays the foundation for designing hybridization reactions with robust, tunable outputs with switch-like responses. This applies to many types of biosensor mechanisms and complex nucleic acid reaction modeling.