However, despite its potential, the application of BO often remains confined to closed-loop optimization based on expensive physical experiments. This limited scope restricts its ability to incorporate alternative sources of information—such as low-fidelity simulations or historical data—that could reduce costs and accelerate discovery (Coley et al., 2020). To address this limitation, multi-fidelity Bayesian optimization (MFBO) has gained increasing interest, integrating low-cost, low-fidelity simulation data with high-fidelity experimental data (Hickman et al., 2025; Peherstorfer et al., 2018). This approach allows for reducing the number of expensive experiments required while maintaining optimization performance, thereby improving sample efficiency and scalability.
The performance of MFBO strongly depends on the surrogate model’s ability to accurately predict the true behaviour of a given system and to generalize across different levels of data fidelity. Selecting models capable of effectively bridging and building upon observations from sources of varying quality therefore lies at the heart of optimal MFBO design. Although Gaussian Process (GP) models have been widely used as surrogate models, they often struggle to scale to high-dimensional and highly nonlinear problems, which may in turn introduce limitations in effectively integrating data across multiple fidelity levels. To address these challenges, we propose a deep neural network (DNN)-based surrogate modeling approach designed to flexibly capture complex, nonlinear relationships while efficiently incorporating multi-fidelity data. In particular, we adopt a transfer learning strategy in which a DNN surrogate model is first pre-trained on a large volume of low-fidelity data—typically obtained from inexpensive and fast simulations—and then fine-tuned using a small number of high-fidelity experimental data points. This approach aims to achieve both scalability and sample efficiency in constructing an accurate surrogate.
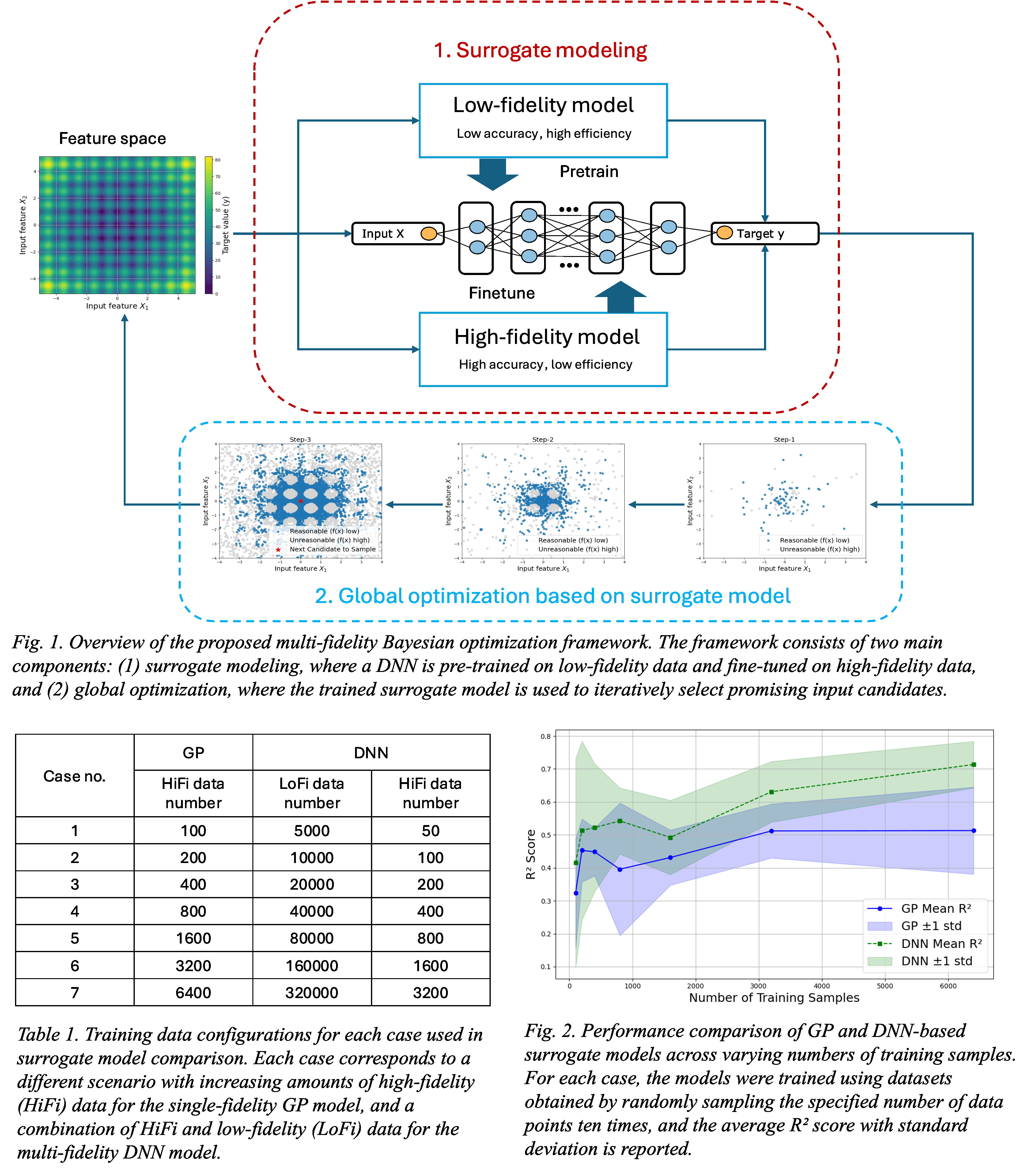
An overview of the proposed framework is illustrated in Fig. 1. As shown, surrogate modeling begins with learning from the low-fidelity model, which offers high efficiency at the cost of lower accuracy. The pretrained surrogate model is subsequently refined by incorporating high-fidelity data that is more accurate but costly to obtain. Once the surrogate model is trained, it is used to guide global optimization in the input feature space to identify the next candidate for evaluation. This work presents the initial phase of the proposed framework, specifically focusing on the surrogate modeling component delineated in Fig. 1. While global optimization constitutes a subsequent step in the full pipeline, the present study aims to establish and validate the multi-fidelity surrogate as a prerequisite for downstream applications.
To evaluate surrogate models for use in multi-fidelity Bayesian optimization (MFBO), we constructed a simulation-based optimization problem for the separation and purification of acetic acid using the BioSteam package for biorefinery process modelling (Cortes-Pena et al., 2020). Two levels of model fidelity were implemented to reflect trade-offs between computational cost and accuracy. In the low-fidelity model, unit operations such as liquid–liquid extraction and distillation were simplified using single-stage and shortcut models, respectively. The high-fidelity model employed rigorous modelling of multi-stage extraction and distillation (MESH equations) columns for more accurate simulation. A toy problem was formulated to minimize the minimum selling price (MSP) of glacial acetic acid, subject to a product purity constraint of at least 98 wt%. Eight decision variables were considered, including the number of extraction stages, the temperature of the heat exchanger, and the recovery ratios of light and heavy key components in each of the three distillation columns.
The effectiveness of surrogate modeling strategies for BO was investigated through a set of controlled experiments comparing single-fidelity and multi-fidelity training schemes. Specifically, we constructed 7 scenarios with increasing amounts of high-fidelity data, ranging from 100 to 6400 samples (see Table. 1). For each case, we compared a baseline model trained solely on high-fidelity data to a multi-fidelity model pre-trained on significantly larger amounts of low-fidelity data and fine-tuned with a smaller subset of high-fidelity samples. Importantly, the dataset configurations were not arbitrary but reflected realistic computational constraints derived from a chemical process simulation benchmark we developed. In this setup, a single run of the low-fidelity model took approximately 0.5 seconds, whereas the high-fidelity model required an average of 167 seconds—over 300 times more expensive. Based on this discrepancy, we designed each scenario such that the total computational time budget remained approximately constant. For instance, in the first case (see Table. 1), generating 20 high-fidelity samples required the same amount of time as generating 300 low-fidelity and 10 high-fidelity samples combined. This setup enables a systematic analysis of sample efficiency, transfer learning effectiveness, and the practical viability of surrogate models under realistic multi-fidelity constraints. Model performance was evaluated using R² score and mean squared error (MSE) between the predictions of each surrogate model and the corresponding ground-truth simulation results across the eight scenarios. For each scenario, the models were trained using datasets generated by randomly sampling the specified number of data points ten times, and the reported R² scores represent the average and standard deviation across these repetitions.
The results summarized in Fig. 2 clearly illustrate that the DNN-based surrogate consistently outperformed the GPR model across all scenarios, with improvements in predictive accuracy becoming increasingly evident as the size of the training dataset grew. The GP model showed modest improvement, with R² values increasing from 0.32 to 0.51 (Δ ≈ 0.19) as the number of training samples increased. In contrast, the DNN model demonstrated a more pronounced enhancement, with R² values rising from 0.41 to 0.72 (Δ ≈ 0.30), suggesting that the DNN surrogate scales more effectively with larger datasets.
Notably, even in Scenario 1, where the amount of high-fidelity data is limited and GP is generally expected to perform well, the transfer learning-based DNN model achieved an R² score that was 0.09 higher than GP. This indicates that the DNN model, when pre-trained on abundant low-fidelity data, can deliver superior predictive performance even with limited high-fidelity samples—highlighting the practical advantage of transfer learning in low-data regimes within multi-fidelity settings.
This performance trend underscores the scalability and effectiveness of the DNN-based surrogate model in multi-fidelity environments. As the availability of low-fidelity data often far exceeds that of high-fidelity data in real-world applications, the ability to leverage transfer learning becomes crucial. The observed improvements suggest that DNN models are better equipped to extract and generalize meaningful patterns from large, albeit less accurate, datasets and subsequently refine these representations with a smaller set of high-fidelity observations. Furthermore, as shown in Fig. 2, the reduced variance in DNN performance across scenarios indicates greater stability compared to GP, which exhibited more fluctuation and saturation under increasing data availability. This stability is particularly advantageous in design tasks where surrogate model predictions are used to guide high-stakes optimization decisions.
In summary, this study highlights the potential of DNN-based surrogate models, particularly those trained using transfer learning, as accurate and scalable alternatives to commonly used GP models. By leveraging abundant low-fidelity data and refining the model with a limited set of high-fidelity samples, the proposed approach enhances predictive performance across selected benchmark scenarios. These results indicate that the method may offer practical value for inverse design systems, especially in contexts where experimental resources are limited and high-fidelity evaluations—such as synthesis or characterization—are costly and time-consuming. Building on this foundation, the current study focuses on validating the surrogate modeling stage using a chemical process simulation-based multi-fidelity optimization task. As a next step, the validated surrogate will be integrated into the closed-loop optimization pipeline (as outlined in Fig. 1) to enable a more realistic assessment of the framework in practical chemical synthesis applications.
References
