(392k) Strengthened Hull Reformulation in Original Space of Linear Generalized Disjunctive Programming (GDP)

Scheduling is a critical aspect of process systems engineering that integrates discrete task sequencing with continuous process variables to optimize plant operations. In recent years, Generalized Disjunctive Programming (GDP) has emerged as a systematic framework for modeling such scheduling problems, enabling the representation of alternative scenarios through disjunctions [1]. Traditionally, solving GDP models involves reformulating them as Mixed-Integer Programming (MIP) problems using either Big-M or hull reformulations. The Big-M method enforces disjunctive logic by applying large constants; however, it typically leads to weaker relaxations due to less tight linear approximations. In contrast, hull reformulation enhances relaxation tightness by disaggregating variables, but it often results in a significant increase in the number of continuous variables, thus potentially increasing computational complexity. Recent advancements in MIP reformulation techniques have demonstrated that strategic improvements, such as multi-parameter Big-M formulations [2]can significantly enhance relaxation quality while reducing model complexity. These innovations reduce the number of branch-and-bound iterations and improve numerical stability by tightening the continuous relaxations of the formulations.

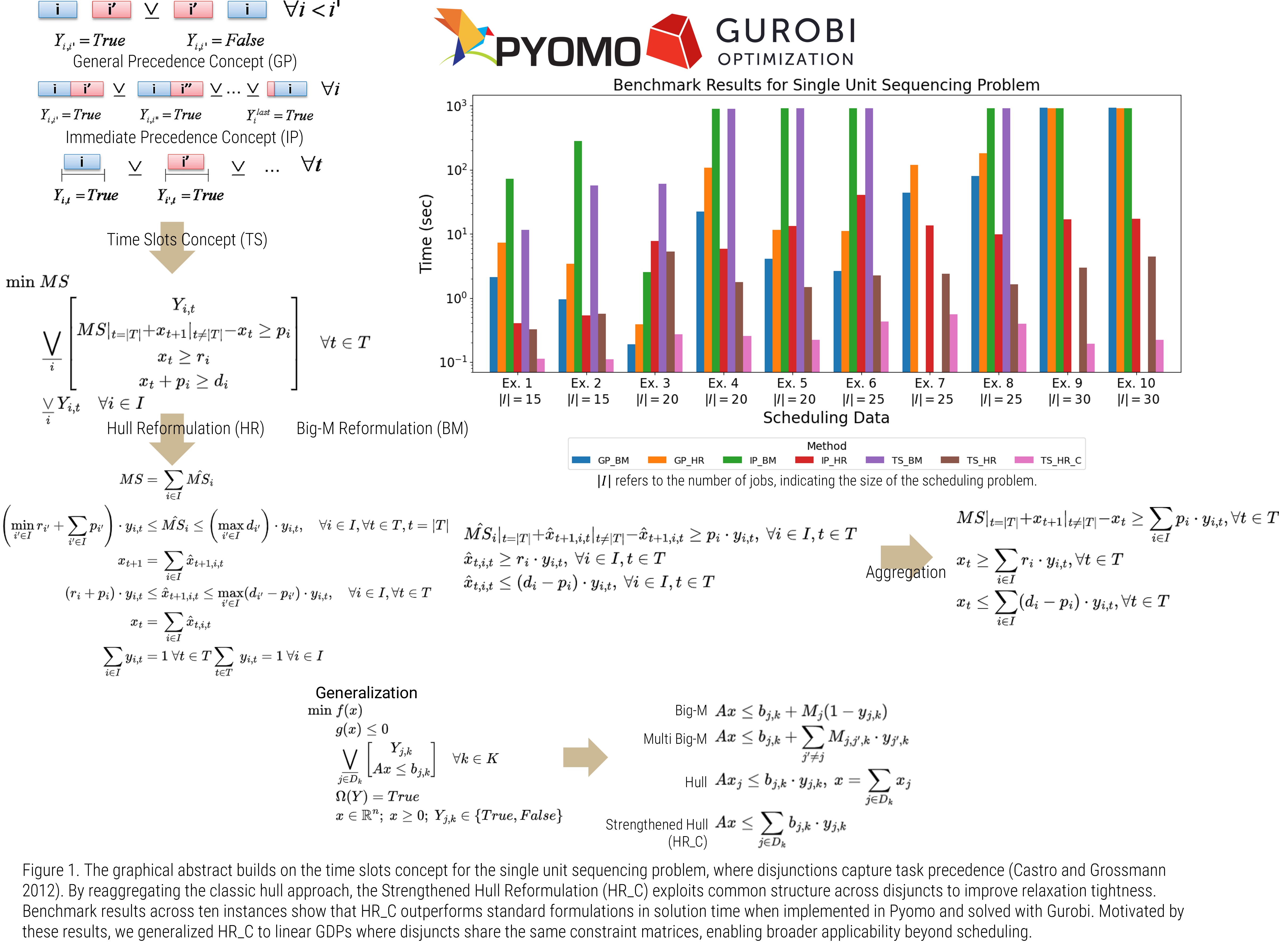
The primary objective of this study is to generalize a more compact and computationally efficient formulation, especially addressing problems described by linear Generalized Disjunctive Programs (GDP) where each disjunct shares identical linear coefficients in constraints but involves right-hand sides. To achieve this, we build upon the concept introduced in [1], where reaggregating variables originally disaggregated by the hull reformulations effectively eliminates unnecessary continuous variables. This formulation was applied to practical scheduling problems, including real-world operating room scheduling case studies [4]. By extending and generalizing this idea beyond single-unit scheduling to broader linear GDP problems, we reconstruct the original decision variables directly within their original space, thereby avoiding the overhead of numerous additional variables. This generalized reformulation preserves the strength of the convex hull relaxation while further reducing model complexity, providing a more efficient and scalable optimization approach suitable for integration into existing MIP frameworks. Such a structure is particularly relevant in cases where the bounds of decision variables are imposed through disjunctive constraints—examples include scheduling applications and energy systems optimization problems that employ box constraints. The MIP framework presented by Kim et al. [4] serves as an illustrative example of this approach. Here, we show that our generalized reaggregation of constraints significantly reduces computational complexity. These advancements lay the groundwork for future research into more efficient optimization algorithms and reformulation strategies in process systems engineering.

References

[1] Castro, P. M., & Grossmann, I. E. (2012). Generalized disjunctive programming as a systematic modeling framework to derive scheduling formulations. Industrial & Engineering Chemistry Research, 51(16), 5781-5792.

[2] Trespalacios, F., & Grossmann, I. E. (2015). Improved Big-M reformulation for generalized disjunctive programs. Computers & Chemical Engineering, 76, 98-103.

[3] Castro, P. M., & Marques, I. (2015). Operating room scheduling with generalized disjunctive programming. Computers & Operations Research, 64, 262-273.

[4] Kim, D., Hong, T., & Piette, M. A. (2022). Generalized Disjunctive Programming-based, Mixed Integer Linear MPC Formulation for Optimal Operation of a District Energy System for PV Self-consumption and Grid Decarbonization: Field Implementation.