(596b) State Observation of a Colloidal Self-Assembly Process with Topological Data Analysis

Feedback control has shown success in guiding the assembly of external field-mediated colloidal self-assembly into specific configurations. [1-8] The essence of a feedback control is to monitor the system state to inform the manipulation of the external field, to handle discrepancy from the target state. Due to its high dimensionality, state representation of the colloidal self-assembly system is normally achieved with dimensionality reduction methods for lower-dimension representations, such as order parameters, calculated from the particle coordinates to capture the structural information of the assembly at a given point of time. These order parameters are typically capable of capturing the configurational features of the assembly but bare no information on the associated kinetics. Such a setup assumes that the evolution of the system in terms of the order parameters is independent off its history, thus claiming the Markovian property. However, such assumption is yet to be validated.

In this study, we present a novel approach that incorporates topological data analysis and a state observer in the form of Kazantzis-Kavaris/Luenberger (KKL) [9], to capture both the configurational features and the temporal dynamics of an electric field-mediated 2-dimensional colloidal self-assembly process. Time series of assembly snapshots will be analyzed with the topological data analysis, to extract state descriptors, and these descriptors will then serve as the inputs to the KKL for temporal dynamics estimation. The KKL observer is comprised of (1) a linear time-invariant dynamics that takes in the measured outputs, i.e. the state descriptors from the topological data analysis, and (2) a nonlinear static map that outputs the state estimates. Specifically, the proposed framework features the following key components.

1. Image Processing: Time series of raw colloidal assembly images are binarized using thresholding, and then individual particles are identified by their contours. The center of each particle is calculated as the centroid of its contour points, generating a 2D point cloud representation of the particle arrangement.
2. Topological Data Analysis: Filtration is performed by expanding circles around the centroid of each particles, and when two circles overlap, we connect these points. This changes the topology of the data representation as the expansion proceeds, resulting in the appearance and disappearance of topological features: connected components (represented by H₀) and holes (represented by H₁) [10]. The radius that topological features that appear and disappear during filtration are known as birth and death respectively within their representative group (H₀, H₁). The key metrics we focus on are the average births and deaths of the homology groups and their variance to capture the static behaviors, as well as the covariance across frames to capture the dynamics. These features are descriptives of the relative crystallinity and the defects within the point cloud.
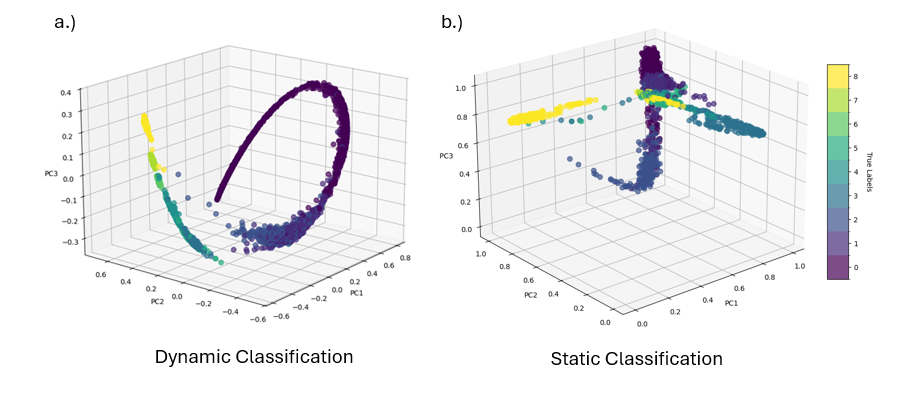
3. KKL Observer: The topological descriptors, considered as process outputs, are fed into a KKL observer [11], which filters the topological descriptors in time by its linear time-invariant dynamics and reconstructs the latent assembly states through a dimensionality reduction algorithm [12] – specifically, kernel principal component analysis is used in this work [12]. Then we perform classification by unsupervised K-means clustering and then validated by true labels . The appended figure shows the projection of the high-dimensional assembly information in the reduced principal components space with (a) and without (b) the observation procedure. Due to the use of the KKL observer, the phase transitions can be visualized as a continuous path in the state space, whereas misclassifications and discontinuities in the transition paths would arise, without the state observation procedure (b).

The framework proposed here can capture the dynamic behavior of the colloidal self-assembly system, thus providing additional process information as compared to the conventional static classification methods. Being capable of both instantaneous classification of the assembly configuration and continuous tracking of the structural development, our framework could enable real-time monitoring of the assembly configurations and their dynamic transitions. We anticipate such functionalities of our framework to further benefit the implementation of advanced process control techniques to colloidal self-assembly, and other crystallization processes.

References

[1] Lizano, A., and Tang, X. (2023). Convolutional neural network-based colloidal self-assembly state classification. J. Soft Matter, 19(19), 3450-3457.

[2] Lizano-Villalobos, A., Namikas, B., and Tang, X. (2024). Siamese neural network improves the performance of a convolutional neural network in colloidal self-assembly state classification. J. Chem. Phys., 161(20), 204905.

[3] Juárez, J. J., and Bevan, M. A. (2012). Feedback controlled colloidal self‐assembly. Adv. Funct. Mater., 22(18), 3833-3839.

[4] Paulson, J. A., Mesbah, A., Zhu, X., Molaro, M. C., and Braatz, R. D. (2015). Control of self-assembly in micro-and nano-scale systems. J. Process Control, 27, 38-49.

[5] Klotsa, D., and Jack, R. L. (2013). Controlling crystal self-assembly using a real-time feedback scheme. J. Chem. Phys, 138(9), 094502.

[6] Tang, X., Rupp, B., Yang, Y., Edwards, T. D., Grover, M. A., and Bevan, M. A. (2016). Optimal feedback controlled assembly of perfect crystals. ACS nano, 10(7), 6791-6798.

[7] Lieu, U. T., and Yoshinaga, N. (2025). Dynamic control of self-assembly of quasicrystalline structures through reinforcement learning. J. Soft Matter, 21(3), 514-525.

[8] Zhang, J., Yang, J., Zhang, Y., and Bevan, M. A. (2020). Controlling colloidal crystals via morphing energy landscapes and reinforcement learning. Sci. Adv., 6(48), eabd6716.

[9] Kazantzis, N., and Kravaris, C. (1998). Nonlinear observer design using Lyapunov’s auxiliary theorem. Syst. Control Lett., 34(5), 241–247.

[10] Smith, A. D., Dłotko, P., and Zavala, V. M. (2021). Topological data analysis: concepts, computation, and applications in chemical engineering. Comput. Chem. Eng., 146, 107202.

[11] Andrieu, V., and Praly, L. (2006). On the existence of a Kazantzis-Kravaris/Luenberger observer. SIAM J. Control Optim., 45(2), 432-456.

[12] Weeks, C., and Tang, W. (2024). Data-Driven Nonlinear State Observation using Video Measurements. IFAC-PapersOnLine, 58(14), 787-792.

Might want to swap the order of the subplots, and add labels (a) and (b) or whatever symbols you would like to use.