(556a) Settling Dynamics of an Individual Spherical Particle in Newtonian and Bingham Fluids

Particle settling and transport in slurries impacts the efficiency and energy demands of mixing and processing operations in various industries, including mineral processing, oil sands extraction, and wastewater treatment. In practice, many industrial fluids exhibit a non-Newtonian behavior with an inherent yield stress. Understanding the settling behavior of the particles in these fluids is crucial in the operation and energy optimization of slurry-based processes. This study investigates the settling dynamics of an individual spherical particle in Newtonian and Bingham fluids utilizing direct numerical simulation (DNS).

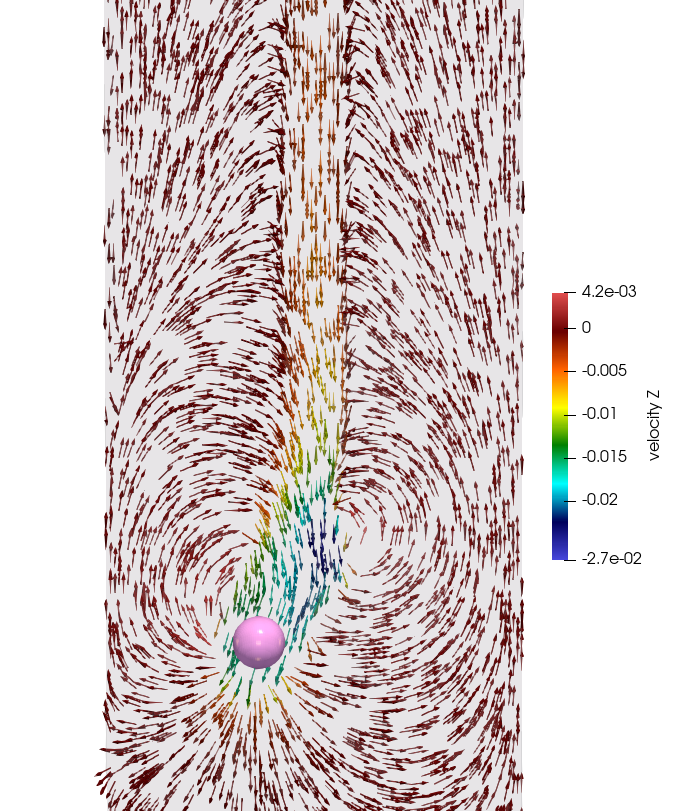
The present work uses the lattice-Boltzmann method (LBM) to numerically solve Navier-Stokes equations. In LBM, the fluid is represented as a distribution of particles on a lattice of discrete nodes where streaming and collision take place at each time step. Bingham fluid behavior was modeled ensuring the particle remains stationary unless the net gravitational force on it exceeds the fluid's yield stress. An immersed boundary method was implemented to model the spherical particle enforcing the no-slip boundary condition at its surface and capturing fluid-particle interactions. In addition, two distinct boundary conditions were studied: wall boundaries with no slip conditions and fully periodic boundary conditions. For both scenarios, the cross sectional area and height of channel were systematically varied to examine the effects of lateral and axial confinement on particle settlement.

The settling behavior of a spherical particle in Newtonian fluids over a broad range of Reynolds numbers is a well-established benchmark. Our simulations results were first validated against the previously published numerical studies for this configurations. Then, We extended the study to examine particle settlement in Bingham fluids by incorporating the Bingham number for yield stress effects, over the same range of Reynolds number and the two boundary conditions. Results from the second part were compared to the available numerical and experimental data.

The simulations were conducted over a wide range of particle Reynolds numbers, from creeping flow conditions (Re < 1) to laminar and transitional flow regimes (Re > 1000). At low Reynolds numbers, particle settling is primarily governed by viscous forces, resulting in predictable, smooth trajectories. As the Reynolds number increases, inertial effects begin to dominate, leading to complex flow structures such as unsteady wakes behind the particle. Capturing this transition from viscosity-driven flow to inertia-driven dynamics was crucial to thoroughly understanding the underlying mechanisms affecting particle settlement under varying fluid rheology and confinement conditions.