(123g) Quantum-Accelerated Reinforcement Learning-Driven Process Synthesis

Industries are continuously advancing through the developments and applications of artificial intelligence (AI) and machine learning (ML) which are revolutionizing the design, optimization, and operations of chemical and energy processes [1]. In the area of process synthesis, reinforcement learning (RL)-driven process design has emerged as a systematic approach to intelligently identify optimal process configurations without relying on prior knowledge or expertise to guide unit operation selection or configuration [2-3]. In this way, the large-scale decision-making process of synthesizing flowsheets and selecting operating variables is robustified since the entire solution space remains for the RL agent to explore [4]. However, this causes a major challenge since it is difficult to manage the computational complexity that arises from the vast combinatorial space, quickly leading to excessively intensive or even intractable problems. Quantum computing, which has been regarded as the new frontier in computing power [5], presents a promising alternative to classical techniques by providing theoretically guaranteed speed-ups [6]. Quantum machine learning (QML) is a specialized approach that harnesses these speed-ups for ML-based tasks. At the center of QML algorithms are parameterized quantum circuits (PQCs), which encode and process data similar to neural networks (NNs) but are able to provide more expressibility with fewer tunable parameters [7-8]. To this end, we propose a novel methodology that integrates QML and RL-driven process synthesis and leverages PQCs and other QML techniques to improve the computational tractability of the synthesis problem while simultaneously accelerating the design space search of the RL agent.

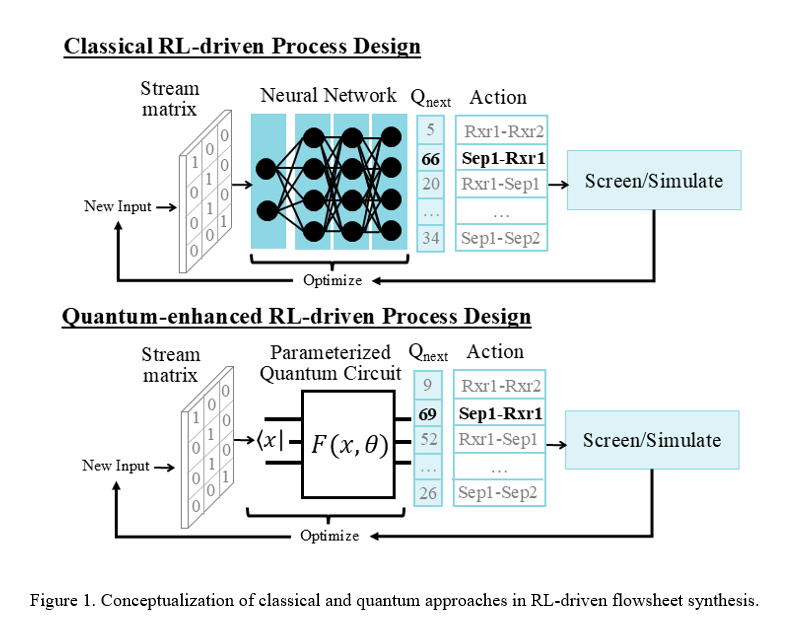
In this work, we build on our prior method of RL-driven process synthesis, which employs a deep q-network (DQN) algorithm to guide an agent in determining the optimal process design [9]. The RL scheme begins with a maximum set of possible unit operations (e.g., two reactors and two distillation columns) that encompass the full design space. The flowsheet structure is represented by stream matrices that encode the input-output relationships between the set of possible operations. This is used as the state in the RL algorithm. The action space comprises all possible manipulations to the flowsheet configuration (e.g., disconnecting or connecting units). The simulation and operating variable selection of flowsheets is done using the IDEAS-PSE platform [10]. DQN uses NNs as Q-function approximators which determine the changes made to the flowsheet matrixes. These are optimized to provide incrementally better flowsheets based on an objective function (e.g., productivity or cost). To integrate QML into this approach, we remove the NNs and replace them with PQCs, as conceptualized in Fig. 1. Special consideration is made to ensure that the observations of the PQC align with the action space of the DQN algorithm. We demonstrate the benefits of integrating QML into RL-driven synthesis through a case study on the hydrodealkylation process. Our results show that the quantum method accelerates the design space search by providing thirteen max reward solutions in one-thousand five-hundred training episodes as compared to nine max reward solutions given by the classical approach. Additionally, the PQC’s provide these solutions with much fewer tunable parameters than the NNs, needing only eighty-eight parameters as opposed to one-thousand ninety-two. This work highlights the need for the exploration of quantum computing, and particularly QML, in process engineering applications. It shows promising results that the implementation of this technology can provide performance benefits with the potential to exceed those provided by classical machine learning.

References:

[1] Braniff, A., Akundi, S. S., Liu, Y., Dantas, B., Niknezhad, S. S., Khan, F., Pistikopoulos, E. N., & Tian, Y. (2025). Real-time process safety and systems decision-making toward safe and smart chemical manufacturing. Digital Chemical Engineering, 100227.

[2] Stops, L., Leenhouts, R., Gao, Q., & Schweidtmann, A. M. (2023). Flowsheet generation through hierarchical reinforcement learning and graph neural networks. AIChE Journal, 69(1), e17938.

[3] Gao, Q., & Schweidtmann, A. M. (2024). Deep reinforcement learning for process design: Review and perspective. Current Opinion in Chemical Engineering, 44, 101012.

[4] Wang, D., Bao, J., Zamarripa-Perez, M. A., Paul, B., Chen, Y., Gao, P., ... & Xu, Z. (2023). A coupled reinforcement learning and IDAES process modeling framework for automated conceptual design of energy and chemical systems. Energy Advances, 2(10), 1735-1751.

[5] Ajagekar, A. & You, F. (2022). New frontiers of quantum computing in chemical engineering. Korean Journal of Chemical Engineering, 39(4), 811–820.

[6] Bernal, D. E., Ajagekar, A., Harwood, S. M., Stober, S. T., Trenev, D., & You, F. (2022). Perspectives of quantum computing for chemical engineering. AIChE Journal, 68(6), e17651.

[7] Jerbi, S., Gyurik, C., Marshall, S., Briegel, H., & Dunjko, V. (2021). Parametrized quantum policies for reinforcement learning. Advances in Neural Information Processing Systems, 34, 28362-28375.

[8] Skolik, A., Jerbi, S., & Dunjko, V. (2022). Quantum agents in the gym: a variational quantum algorithm for deep q-learning. Quantum, 6, 720.

[9] Tian, Y., Akintola, A., Jiang, Y., Wang, D., Bao, J., Zamarripa, M. A., Paul, B., Chen, Y., Gao, P., Noring, A., Iyengar, A., Liu, A., Marina, O., Koeppel, B., Xu, Z. (2024). Reinforcement Learning-Driven Process Design: A Hydrodealkylation Example. Systems and Control Transactions, 3, 387-393.

[10] Lee, A., Ghouse, J. H., Eslick, J. C., Laird, C. D., Siirola, J. D., Zamarripa, M. A., ... & Miller, D. C. (2021). The IDAES process modeling framework and model library—Flexibility for process simulation and optimization. Journal of advanced manufacturing and processing, 3(3), e10095.