(91a) Probing Inclined Plane Flow of Highly Deformable Particles Using a Novel Calibration-Less Bonded-Sphere Model

Dense granular media flowing down an inclined plane are frequently encountered in nature (e.g., landslides) and in industrial processes (e.g., discharging operations). Previous research on these systems has predominantly focused on rigid particles.^1,2 The flow of deformable particles such as rubber and microgels has received significantly less attention despite their practical relevance^3,4. This work aims to address this gap by modelling highly deformable particles and elucidating their peculiar physics when flowing down inclined planes.

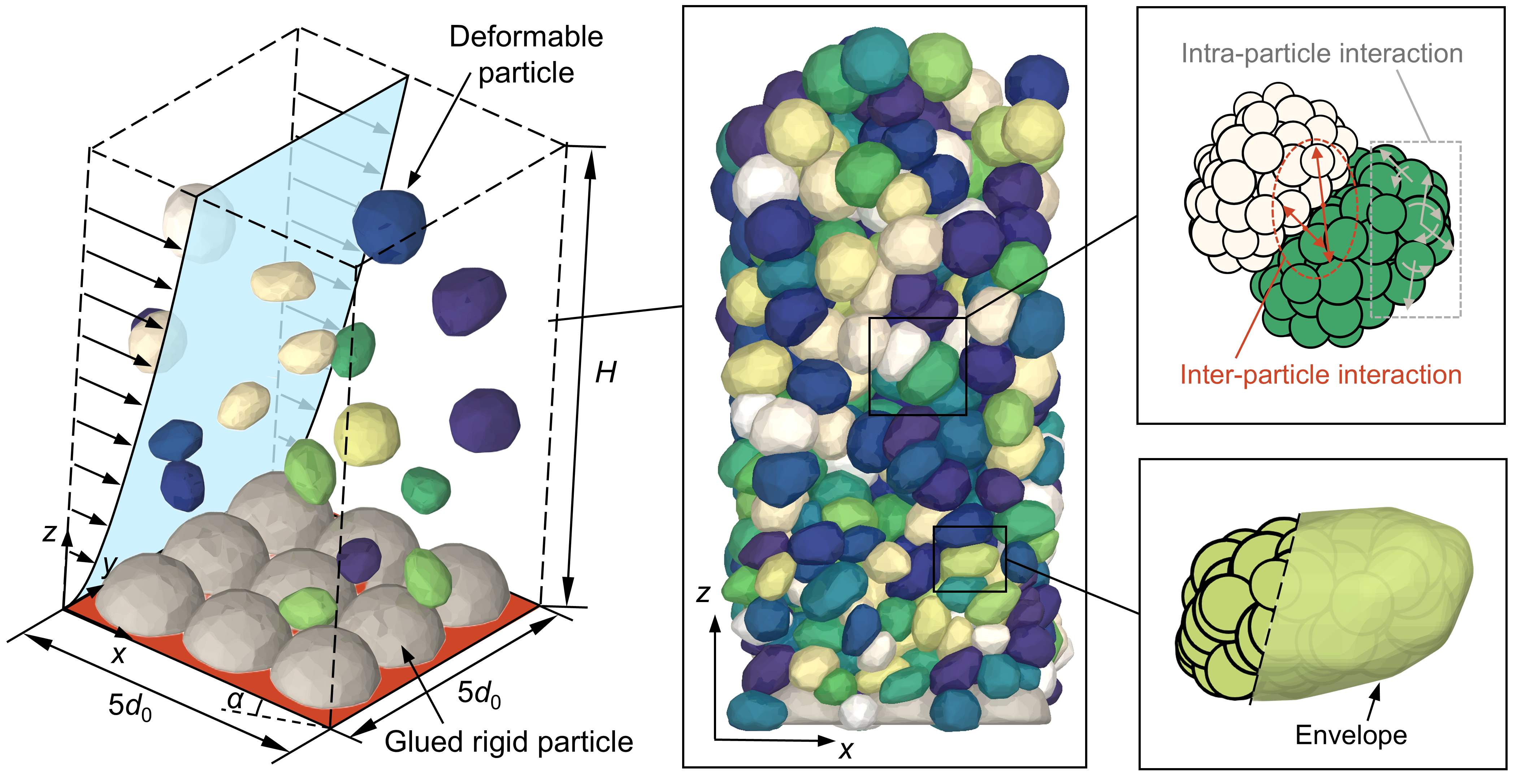
To this end, a bonded-sphere model based on the discrete element method (DEM) is developed that allows for the simulation of highly deformable, linear-elastic particles. Voronoi-tessellation is employed to segment an arbitrarily shaped particle into a network of sub-spheres connected via virtual bonds. This network accurately mimics the mechanical properties of the deformable particle independent of the number (within certain limits) and arrangement of the sub-spheres, making the model calibration-less. Inter-particle collisions are resolved by considering contacts between the respective, contacting sub-spheres. The proposed model is carefully validated using well-established single- and multi-particle benchmark scenarios.

Subsequently, the model is applied to investigate the effect of inclination angle (α) and Young’s modulus (E) on the rheology of inclined plane flows. The parameter p/E is introduced to describe particle deformation, where p is the local granular pressure. For p/E < ~0.1, a mild particle deformation occurs increasing the flowability of the particles as seen by an increased inertial number near the bottom. However, for p/E > ~0.1, the inertial number decreases and the particles exhibit high coordination numbers, indicating a jamming of the flow. Additionally, we observe deformed particles to orient at a certain angle with regard to the main flow; this behaviour is similar to the orientational ordering found for rigid, non-spherical particles⁵. The orientation angle is a function of p/E, but independent of the inertial number and α.

References

1. L.E. Silbert, D. Ertaş, G.S. Grest, T.C. Halsey, D. Levine, and S.J. Plimpton, Phys. Rev. E, 5, 64 (2001).
2. V. Kumaran, J. Fluid Mech., 599 (2008).
3. H.P. Kuo, Y.C. Hsiao, and P.Y. Shih, Powder Technol., 3, 166 (2006).
4. M.L. Manning, Phys. Rev. Lett., 13, 130 (2023).
5. T. Börzsönyi, B. Szabó, G. Törös, S. Wegner, J. Török, E. Somfai, T. Bien, and R. Stannarius, Phys. Rev. Lett., 22, 108 (2012).