(643e) Optimizing Reverse Electrodialysis Design and Operation for Renewable Electricity Generation from Salinity Gradients

Implementing reverse electrodialysis (RED) to tap into salinity gradient energy (SGE) provides a viable approach to producing sustainable electricity [1]. Major strides in RED rely on in-depth techno-economic studies covering the entire process design and operational space. Yet, estimating the costs and performance of RED is difficult due to its intricate configuration and operational decisions. Generalized Disjunctive Programming (GDP) models are valuable for identifying optimal conditions in complex designs using higher-level logic, resulting in better-structured optimization models and solution strategies [2]. In earlier research, we developed a GDP that incorporates a RED stack predictive model, whose solution provides a flowsheet design that maximizes the net present value (NPV) for a specific stack design, feed stream properties, and financial parameters [3,4]. In RED pilot trials, modules are typically shaped to be either elongated or square [5–7]. The premise of this research is that modules designed with a greater width than length can improve system performance and handle larger feed volumes with fewer, more powerful units, all while having the same membrane area. Hence, we can foresee more streamlined, compact, and cost-effective systems. To explore this, we add size and width-to-length ratio as variables in the GDP. We derived a tractable RED unit model for GDP in prior work [3], relying on assumptions from a validated differential-algebraic model [8,9] that may not reflect the current sizes and shapes in the study. We revisit these approximations to refine the model, ensuring it remains precise yet tractable for all shapes and sizes in the assessments. We selected the energy recovery from salinity differences between desalination brine and treated wastewater as a case study, addressing the environmental impact of carbon emissions and brine disposal while promoting circularity [4]. The GDP model is coded using the Python-based, algebraic modeling language Pyomo [10] and Pyomo.GDP library for logic-based modeling and optimization [11] and solved with the Global Logic-based Outer Approximation (GLOA) algorithm [12,13] implemented in GDPopt [13]. We decided on Aspen Custom Modeler (ACM) to implement and solve the differential-algebraic RED unit model. We run simulations, excluding each deviation from the accurate model to discern the primary error source; the resistance from the streamwise concentration gradient has the major relative contribution, accounting for 39% of the variation in the smallest square module, which rises to 54% as the size and flow path increase. When this resistance is factored into the Pyomo RED stack model, it results in more reliable predictions for ACM simulations. Upon validation, we solve the refined GDP model with modules of different sizes and aspect ratios. In terms of size, larger units generate higher profits because of economies of scale and increased net power relative to their smaller counterparts. No matter its size, a wider-than-long stack can bring higher profits, making it a more financially sound alternative to a square design. For any size and shape, the optimization model yields financially viable process designs that earn 0.5–2.5 million $ in net profits with a levelized cost of energy (LCOE) of $115–169 MWh-1. The optimal flowsheet comprises eleven 6 m² stacks with a 6:1 aspect ratio, delivering a net power capacity of 283 kW and an energy conversion efficiency of 27%. This design allows desalination plants to cut greenhouse gas emissions from the grid by 6% affordably while providing an economical way to handle brine. This systematic assessment of different sizes and channel dimensions is designed to give practical design and operational advice for manufacturers and decision-makers at all RED unit and process development stages. We found that the GDP model might support the effective implementation and rollout of RED projects in the water sector.

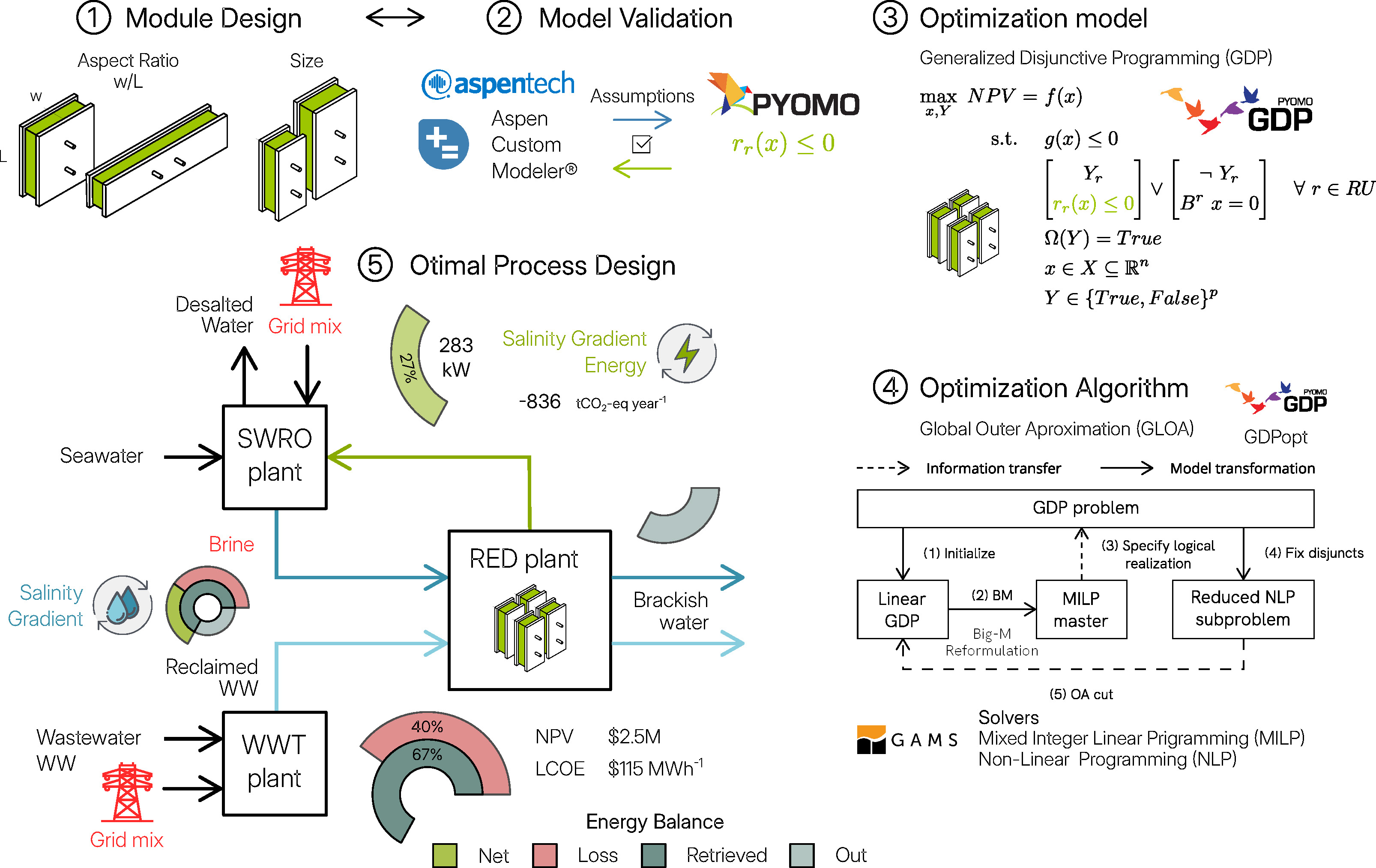
Figure 1 Impact of scaling and shape of RED units on the optimal design and techno-economic assessment of reverse electrodialysis (RED) plant drawing electricity from the salinity gradient between seawater reverse osmosis (SWRO) desalination brine and reclaimed wastewater (WW) effluent from a WW treatment plant.

References

[1] S. Chae, H. Kim, J. Gi Hong, J. Jang, M. Higa, M. Pishnamazi, J.Y. Choi, R. Chandula Walgama, C. Bae, I.S. Kim, J.S. Park, Clean power generation from salinity gradient using reverse electrodialysis technologies: Recent advances, bottlenecks, and future direction, Chem. Eng. J. 452 (2023) 139482. https://doi.org/10.1016/J.CEJ.2022.139482.

[2] Q. Chen, I.E. Grossmann, Recent Developments and Challenges in Optimization-Based Process Synthesis, Https://Doi.Org/10.1146/Annurev-Chembioeng-080615-033546 8 (2017) 249–283. https://doi.org/10.1146/ANNUREV-CHEMBIOENG-080615-033546.

[3] C. Tristán, M. Fallanza, R. Ibáñez, I. Ortiz, I.E. Grossmann, A generalized disjunctive programming model for the optimal design of reverse electrodialysis process for salinity gradient-based power generation, Comput. Chem. Eng. 174 (2023) 108196. https://doi.org/https://doi.org/10.1016/j.compchemeng.2023.108196.

[4] C. Tristán, M. Fallanza, I. Ortiz, R. Ibáñez, I.E. Grossmann, Cost-optimal design of reverse electrodialysis process for salinity gradient-based electricity generation in desalination plants, Energy 313 (2024) 134005. https://doi.org/10.1016/J.ENERGY.2024.134005.

[5] M. Tedesco, A. Cipollina, A. Tamburini, G. Micale, Towards 1 kW power production in a reverse electrodialysis pilot plant with saline waters and concentrated brines, J. Memb. Sci. 522 (2017) 226–236. https://doi.org/10.1016/j.memsci.2016.09.015.

[6] R.A. Tufa, S. Pawlowski, J. Veerman, K. Bouzek, E. Fontananova, G. di Profio, S. Velizarov, J. Goulão Crespo, K. Nijmeijer, E. Curcio, Progress and prospects in reverse electrodialysis for salinity gradient energy conversion and storage, Appl. Energy 225 (2018) 290–331. https://doi.org/10.1016/J.APENERGY.2018.04.111.

[7] M. Yasukawa, S. Mehdizadeh, T. Sakurada, T. Abo, M. Kuno, M. Higa, Power generation performance of a bench-scale reverse electrodialysis stack using wastewater discharged from sewage treatment and seawater reverse osmosis, Desalination 491 (2020) 114449. https://doi.org/10.1016/j.desal.2020.114449.

[8] C. Tristán, M. Fallanza, R. Ibáñez, I. Ortiz, Recovery of salinity gradient energy in desalination plants by reverse electrodialysis, Desalination 496 (2020) 114699. https://doi.org/10.1016/j.desal.2020.114699.

[9] R. Ortiz-Imedio, L. Gomez-Coma, M. Fallanza, A. Ortiz, R. Ibañez, I. Ortiz, Comparative performance of Salinity Gradient Power-Reverse Electrodialysis under different operating conditions, Desalination 457 (2019) 8–21. https://doi.org/10.1016/J.DESAL.2019.01.005.

[10] W.E. Hart, C.D. Laird, J.-P. Watson, D.L. Woodruff, G.A. Hackebeil, B.L. Nicholson, J.D. Siirola, Pyomo — Optimization Modeling in Python, Second Edi, Springer International Publishing, Cham, 2017. https://doi.org/10.1007/978-3-319-58821-6.

[11] Q. Chen, E.S. Johnson, D.E. Bernal, R. Valentin, S. Kale, J. Bates, J.D. Siirola, I.E. Grossmann, Pyomo.GDP: an ecosystem for logic based modeling and optimization development, Optim. Eng. 23 (2022) 607–642. https://doi.org/10.1007/s11081-021-09601-7.

[12] S. Lee, I.E. Grossmann, A global optimization algorithm for nonconvex generalized disjunctive programming and applications to process systems, Comput. Chem. Eng. 25 (2001) 1675–1697. https://doi.org/10.1016/S0098-1354(01)00732-3.

[13] Q. Chen, E.S. Johnson, J.D. Siirola, I.E. Grossmann, Pyomo.GDP: Disjunctive Models in Python, in: Comput. Aided Chem. Eng., Elsevier B.V., 2018: pp. 889–894. https://doi.org/10.1016/B978-0-444-64241-7.50143-9.