(390at) Optimization-Based Membrane System Synthesis for Liquid Separations

Industrial separation technologies, such as distillation, are highly energy-intensive and account for a significant portion of the total energy consumption in U.S. industrial processes. Membrane-based separation is widely regarded as a promising technology for diverse industrial applications, including organic solvent recovery, oil and water separation, and seawater desalination. Polymeric membranes are a favorable choice due to their scalability in manufacturing and adaptability to surface modifications. Two key characteristics of polymeric membranes are selectivity and permeability – where higher permeability yields high recovery and higher selectivity enables high purity. However, polymeric membranes exhibit an inherent tradeoff between selectivity and permeability [1]. As a result, utilizing a single-stage membrane system often proves infeasible or leads to increased operating and capital costs when striving to achieve high recovery and purity simultaneously. To overcome this limitation, it is essential to synthesize multi-stage membrane network systems.

Numerous membrane network configurations, characterized by distinct stream connections and multiple membrane stages, can be synthesized to achieve specific separation tasks. However, the energy requirements and capital expenditures associated with these configurations may vary considerably. These variations depend on operating conditions, the number of membrane stages, and the overall required membrane area [2]. Therefore, the economic feasibility of membrane separation critically depends on the decisions made during membrane network synthesis.

In a generalized membrane network synthesis problem, we are given: (1) the molar flowrates of a liquid mixture feed stream, (2) membrane permeances for each component, and (3) desired recovery and purity specifications for target components. Simulation-based methods are often employed to synthesize membrane networks, where a network is selected from numerous potential network configurations and then its operating conditions are determined [3]. However, as the number of membrane stages increases, this method becomes increasingly inefficient because the potential network configurations grow dramatically. Consequently, only a limited number of network configurations can be examined, which may lead to suboptimal networks.

To address this challenge, we propose a novel, generalized mathematical framework for an optimization model that synthesizes membrane networks to recover multiple components from a liquid mixture [4]. The optimization framework encompasses three key elements: (1) the crossflow membrane unit model, (2) a rich membrane network superstructure, and (3) a mixed-integer nonlinear programming (MINLP) model.

In this work, we focus on crossflow membrane separation via pervaporation, where a partial vacuum is maintained on the permeate-side to enhance the driving force for mass transfer. The crossflow membrane unit model, formulated as a differential-algebraic equation (DAE) system by Shindo et al., is widely employed for both gas and liquid separation [5]. However, integrating a DAE system into an optimization model to achieve a globally optimal solution remains challenging [6]. Therefore, we adopt an alternative approach by assuming a uniform collective driving force and uniform activity coefficients across the membrane surface. Additionally, we utilize the concept of control parameterization to discretize the control space by approximating the control function with a linear combination of basis functions [7]. As a result, we reformulate the DAE model into a physics-based algebraic nonlinear surrogate membrane unit model (NLAE).

We propose a superstructure with extensive interconnections designed to recover multiple target components from a liquid mixture, encompassing all potential network configurations. This superstructure comprises distinct interconnected sub-networks to facilitate the overall separation. Each sub-network employs a specific membrane material, engineered for the selective separation of a target component. Within a sub-network, from each stage, the retentate/permeate stream can be: (1) bypassed to subsequent stages (bypass stream), (2) recycled to previous stages (recycle stream), or (3) collected as the product (product stream). The permeate final product stream from each sub-network contains the recovered target component, while the retentate final product stream is directed to other sub-networks for further separation. Further, to avoid symmetrical solutions, the fresh feed is allowed to enter only at the first stage of a sub-network.

Next, we formulate a MINLP model using integer and continuous variables to represent configurational and operational decisions, respectively. The resulting optimization model is a nonconvex MINLP, which is generally difficult to solve to global optimality. Therefore, we introduce variable bounds and tightening constraints to improve computational efficiency. The optimization model determines the optimal membrane network configuration together with operating conditions that minimize the overall required membrane area.

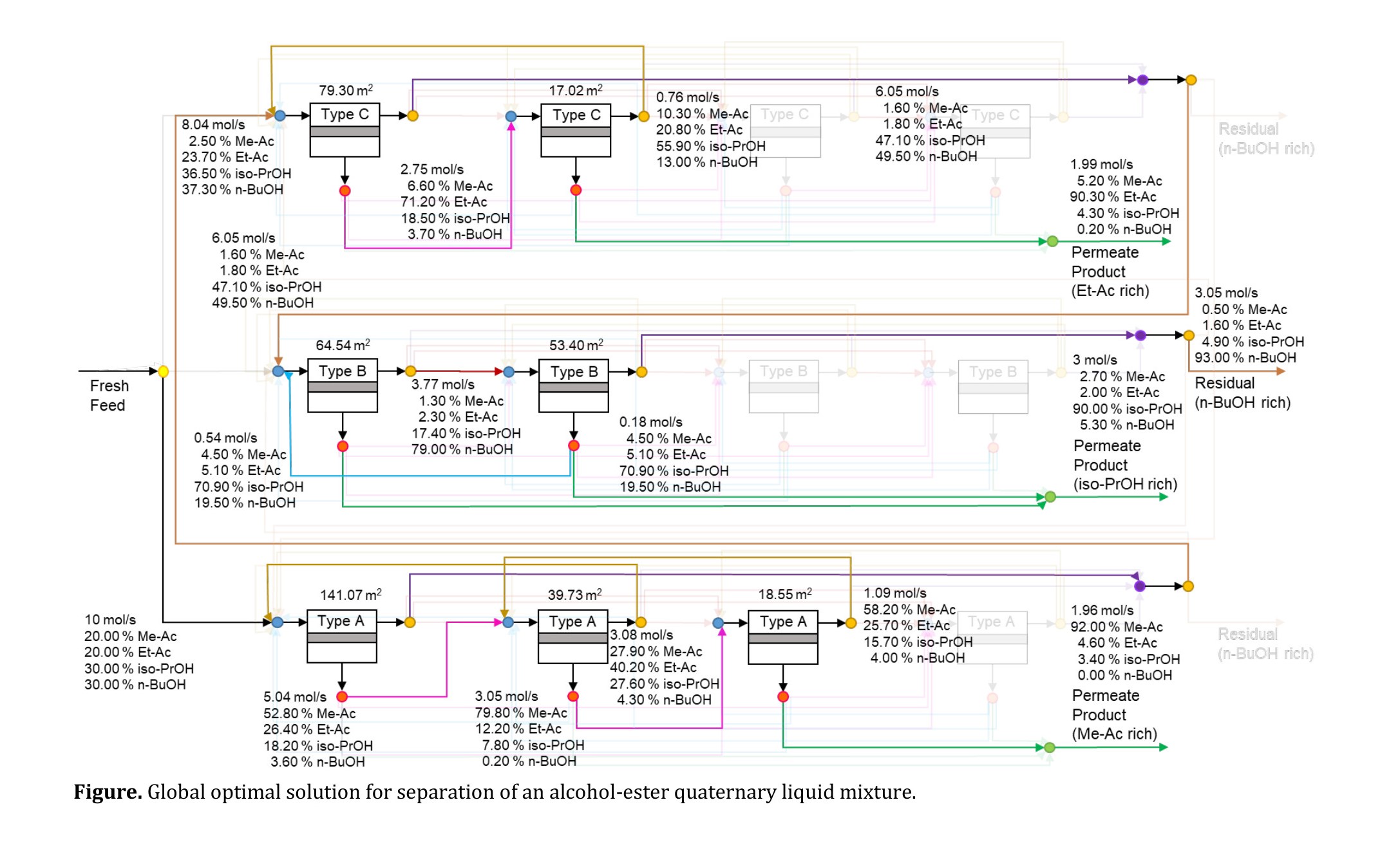
We present multiple applications that demonstrate the applicability of our framework. First, we study the separation of one and two components from an alcohol/water mixture, while varying the recovery and purity specifications for the target component. Additionally, we identify the major drivers by studying the impact of the desired recovery and purity for the target component on the number of required stages and the minimum required total membrane area. Second, we present the membrane network synthesis for the separation of all four components from an alcohol-ester quaternary liquid mixture by utilizing a superstructure incorporating three distinct interconnected sub-networks with distinct materials, each with four available stages. The optimal network is illustrated in the given figure.

References

[1] L.M. Robeson, The upper bound revisited, J. Membr. Sci. 320 (2008) 390–400. https://doi.org/10.1016/j.memsci.2008.04.030.

[2] R. Spillman, Chapter 13 Economics of gas separation membrane processes, in: R.D. Noble, S.A. Stern (Eds.), Membr. Sci. Technol., Elsevier, 1995: pp. 589–667. https://doi.org/10.1016/S0927-5193(06)80015-X.

[3] R. Agrawal, J. Xu, Gas-separation membrane cascades utilizing limited numbers of compressors, AIChE J. 42 (1996) 2141–2154. https://doi.org/10.1002/aic.690420806.

[4] H. Verma, D. Jassby, C.T. Maravelias, Superstructure-based optimization of membrane network systems for multicomponent liquid mixture separation, J. Membr. Sci. 717 (2025) 123574. https://doi.org/10.1016/j.memsci.2024.123574.

[5] Y. Shindo, T. Hakuta, H. Yoshitome, H. Inoue, Calculation Methods for Multicomponent Gas Separation by Permeation, Sep. Sci. Technol. 20 (1985) 445–459. https://doi.org/10.1080/01496398508060692.

[6] J.K. Scott, P.I. Barton, Reachability Analysis and Deterministic Global Optimization of DAE Models, in: A. Ilchmann, T. Reis (Eds.), Surv. Differ.-Algebr. Equ. III, Springer International Publishing, Cham, 2015: pp. 61–116. https://doi.org/10.1007/978-3-319-22428-2_2.

[7] Q. Lin, R. Loxton, K.L. Teo, The control parameterization method for nonlinear optimal control: A survey, J. Ind. Manag. Optim. 10 (2013) 275–309. https://doi.org/10.3934/jimo.2014.10.275.