(601c) Onset of Transition Due to Fluid-Structure Interaction at Low Reynolds Number during Flow through Deformable Microchannels

The study of flow past flexible walls exhibits qualitatively distinct characteristics compared to flow over rigid surfaces. The elastic nature of tube walls and the resulting fluid–structure interaction in deformable channels have made this a subject of significant research interest. In such systems, the fluid-induced stresses deform the solid boundary, and this deformation, in turn, influences the fluid flow. Various studies indicate that wall deformation can lead to flow transition at Reynolds numbers (Re) significantly lower than 2000 for rigid tubes.

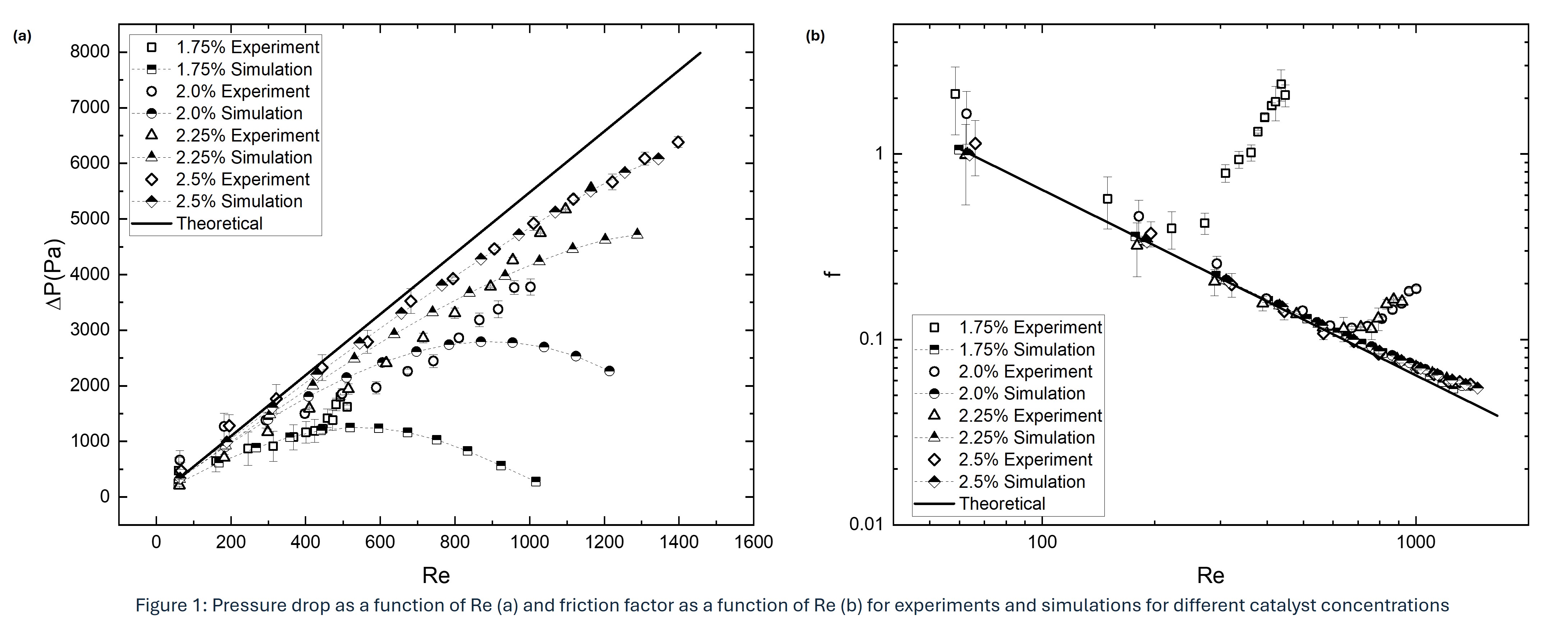
In this work, we investigate flow-induced instabilities in a circular tube with flexible walls. Numerical simulations were performed using COMSOL Multiphysics 6.2, employing the Fluid Flow (Laminar) and Structural Mechanics (Nonlinear Structural Materials) modules. The fluid–structure interaction in our model was governed by Poisson’s ratio and Lamé parameters. We examined pressure drop and channel deformation in the test section of the microchannel as functions of Re. Since the flow was modelled as laminar, deviations in the pressure drop from theoretical predictions signified the onset of transition. Our results show that the critical Reynolds number for transition in a deformable microchannel is substantially lower than that for a rigid tube. The interaction is such that the flow-induced pressure causes wall expansion, which in turn imposes additional pressure on the downstream flow, thereby inducing transition. The transition in microchannels was directly proportional to the Lamé parameter values in the test section.

To validate the simulation results, we also performed experiments. The deformable microchannels were fabricated by casting tubes of approximately same geometric parameters in polydimethylsiloxane (PDMS) gels, with varying catalyst concentrations to replicate the range of storage moduli used in the simulations. A constant pressure-driven flow was maintained inside the microchannel and both pressure drop and friction factor were measured as functions of Re. Experimental data revealed that laminar flow becomes unstable at a relatively low Reynolds number (~300) for the softest channels. The f versus Re curves also differed qualitatively from those for rigid tubes. While the friction factor in rigid tubes rises sharply at the transition point, in flexible tubes it increases continuously from its laminar value of 16/Re. Oscillations in the tube wall were also observed at the onset of transition, indicating that coupling between viscous fluid stresses and elastic wall stresses leads to flow instability. Experimental findings were in good agreement with simulation results. The atypical transition behaviour observed is primarily attributed to wall flexibility and, to a lesser extent, to microchannel geometry.