2025 AIChE Annual Meeting
(642h) Multi-Fidelity Bayesian Optimization for Computer Aided Solvent Design
Authors
Determining reaction rate constants experimentally is costly [3]. Consequently, Computer-Aided Molecular Design (CAMD) methods have been employed for solvent screening in reactions for the past 30 years. Recent advancements have significantly improved the accuracy of these methods by incorporating Quantum Chemistry (QM) calculations [4, 5]. However, this enhanced accuracy comes at the cost of considerably increased computational expense, as accurate QM models require substantial computational resources to solve. This trade-off highlights the need for reliable yet low-cost predictive approaches.
Multi-Fidelity Bayesian Optimization (MFBO) has shown promise in managing the computational cost, even when dealing with discrete decisions such as the choice of material [6]. This capability is particularly useful when applied to certain classes of QM methods, which are inherently hierarchical as their computational cost scales with the desired level of accuracy or fidelity. In this work, we present an MFBO-QM-CAMD approach that leverages the cost efficiency of MFBO while exploiting the cost-accuracy trade-off of such QM methods.
The MFBO algorithm relies on a surrogate model and an acquisition function. The surrogate model, a Gaussian Process (GP), maps a design space of solvent candidates and information of the fidelity of the models to the objective function (here, the logarithm of the reaction rate constant). The acquisition function employs Augmented Expected Improvement (AEI), balancing information gain and computational cost through covariance- and cost-ratio-based penalties. A distance-based kernel is used for the material design space and a non-stationary kernel for model fidelity. We assess several functional forms for these kernels, including the functions adopted in [6], as well as different formulations of the MFBO acquisition function.
The MFBO framework balances computational cost and accuracy by employing various combinations of high- and low-accuracy methods. An exemplary combination of QM methods is the adoption of the 31+G(d) level of theory and basis set for high-fidelity following [5], and the HF/3-21G* level of theory and basis set, a mean-field method neglecting explicit electron correlation for low-fidelity. The varying level of sophistication is reflected in the computational cost of each method, with M062X/6-31+G(d) being about 66 times more expensive than HF/3-21G*. The selection of an initial dataset can impact of the performance of Bayesian Optimization (BO) algorithms, so we use randomly initial data points and present performance statistics over 10 runs. We also compare this to a systematic approach to initial dataset selection based on model-based design of experiments.
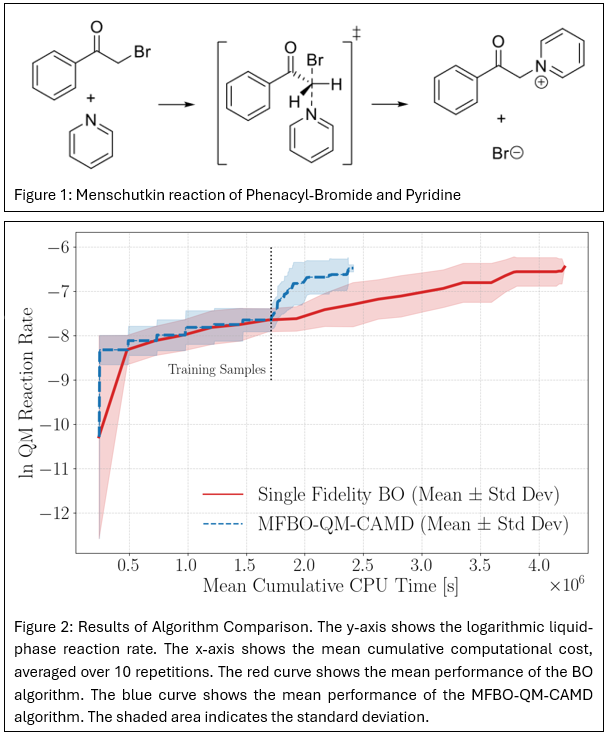
The performance of the MFBO-QM-CAMD approach is assessed on multiple case-studies. Presented here are the results for maximizing the liquid-phase reaction rate constant for a Menschutkin reaction. Menschutkin reactions, in which a tertiary amine reacts with an alkyl halide to form a quaternary ammonium salt are significantly influenced by the reaction medium, as reflected in measured rate constants in different solvents [7]. The specific reaction considered here is shown in Figure 1.
We compare the performance of different formulations of the acquisition function and of different combinations of high- and low-fidelity models. The MFBO-QM-CAMD approach is found to be more effective than single-fidelity BO. An example of this is shown in Figure 2 with the acquisition function and kernels used in [6], M062X/6-31+G(d) as the high-fidelity model and HF/3-21G* as the low-fidelity model. The single-fidelity BO approach uses the Expected Improvement acquisition function (EI). Both curves only show the high-fidelity objective function observations of the logarithm of the rate constant, so that the areas where the objective function remains constant correspond to iterations where low-fidelity sampling is conducted. Both algorithms are given an initial set of data for 7 solvents and a budget of 128 iterations in total.
In the presented example, MFBO-QM-CAMD is found to identify the top-solvent after evaluations on average in addition to the 7 evaluations required to generate the initial data. The single-fidelity BO approach identifies the top solvent after 11 high-fidelity evaluations in addition to the generation of the initial data. In total, a cost reduction of 43 % is achieved by the MFBO approach.
Our work shows that MFBO-QM-CAMD is promising in accelerating solvent design by minimizing computational expense. The algorithm strategically samples low-accuracy QM models to explore the objective function and navigates towards high-accuracy QM models based on a cost-information trade-off. MFBO-QM-CAMD is evaluated using QM models tested for both solution quality and computational cost, as well as several acquisition functions, kernel designs, and CAMD case studies, highlighting its potential for efficient solvent screening.
[1] Grom, M., Stavber, G., Drnovšek, P. & Likozar, B. Modelling Chemical Kinetics of a Complex Reaction Network of Active Pharmaceutical Ingredient (API) Synthesis with Process Optimization for Benzazepine Heterocyclic Compound. Chemical Engineering Journal 283, 703–716. issn: 13858947. (2016)
[2] N.Borhani, T. & Wang, M. Role of Solvents in CO2 Capture Processes: The Review of Selection and Design Methods. Renewable and Sustainable Energy Reviews 114, 109299. issn: 13640321. (2019)
[3] Folic, M. & Adjiman, C. S. Computer-Aided Solvent Design for Reactions: Maximizing Product Formation. Industrial & Engineering Chemistry Research 47(15), 5190-5202 (2008)
[4] Struebing, H. et al. Computer-Aided Molecular Design of Solvents for Accelerated Reaction Kinetics. Nature Chemistry 5, 952–957. issn: 1755-4330, 1755-4349. (2013)
[5] Gui, L. et al. Integrating Model-Based Design of Experiments and Computer-Aided Solvent Design. Computers & Chemical Engineering 177, 108345. issn: 00981354. (2023)
[6] Gantzler, N., Deshwal, A., Doppa, J. R. & Simon, C. M. Multi-Fidelity Bayesian Optimization of Covalent Organic Frameworks for Xenon/Krypton Separations. Digital Discovery 2, 1937– 1956. issn: 2635-098X. (2023).
[7] Reinheimer, J. D., Harley, J. D., Meyers, W. M. Solvent Effects in the Menschutkin Reaction | Journal of Organic Chemistry (1963)