(681a) Multi-Fidelity Bayesian Optimization Using Global Optimization

High-fidelity models are often required to optimize operations for dynamical systems characterized by complex dynamics. However, such models [2, 3, 4] can be computationally expensive to evaluate, and their evaluation is often a bottleneck in their use for optimization. Active learning techniques like BO [5] intelligently sample design spaces for such high-fidelity models in hopes of minimizing the number of expensive model evaluations made during optimization. To further accelerate/improve the optimization scheme, we can also leverage a lower-fidelity model to gain useful information about the high-fidelity space while reducing the overall computational expense.

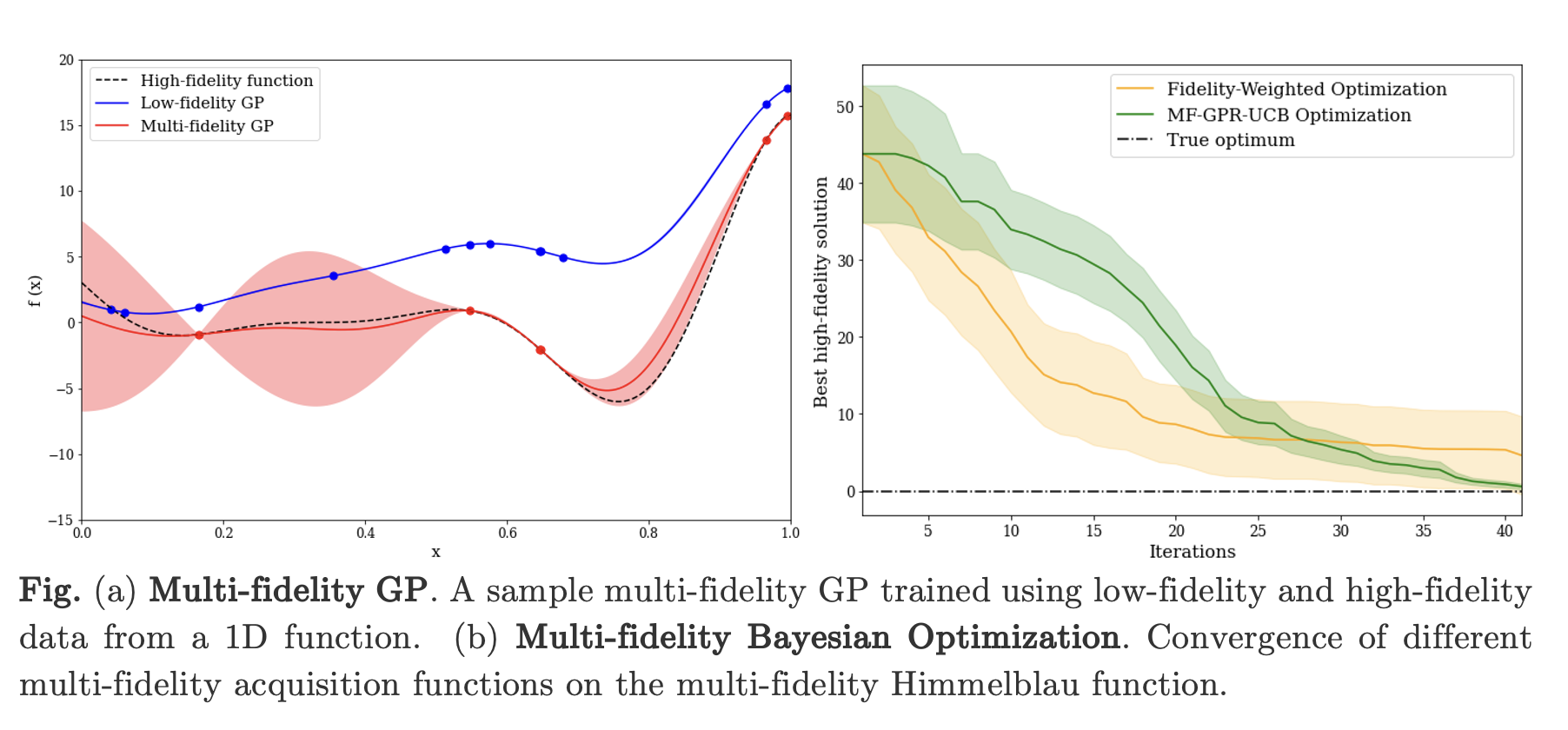
Recent research [4] highlights the use of multi-fidelity Gaussian Processes (GPs) [6, 7], hierarchical models that combine a low-fidelity GP with a correction GP, as surrogate models. This enhances model flexibility by accounting for the discrepancy between the high-fidelity and low-fidelity model- and better capturing complex behavior. Sapsis et al. combined a multi-fidelity GP with a fidelity-weighted [2] acquisition function. The fidelity-weighted approach adjusts the acquisition function using a cost-ratio penalty term to account for the significant difference in computational expense between the high-fidelity and low-fidelity functions. However, further studies highlighted poor information exchange between the low-fidelity and high-fidelity models with this approach. Kandasamy et al. propose an intuitive multi-fidelity acquisition function [8] based on Upper Confidence Bounds (UCB) which exhibits better information exchange. However, instead of a multi-fidelity GP, they utilize a standard GP as the high-fidelity surrogate model, constructed solely from the high-fidelity data. To improve upon existing multi-fidelity approaches, we propose a framework which combines multi-fidelity GPs with the multi-fidelity UCB as the acquisition function.

Just like standard acquisition functions, multi-fidelity acquisition functions often exhibit a multimodal landscape - so that the exploitative component of the acquisition function develops multiple local optima. For explorative acquisition functions, uncertain regions result in additional local optima. Commonly used strategies to mitigate local optima, like the multi-start L-BFGS-B, initialize a local solver from multiple starting points. However, these approaches do not guarantee convergence to the global optimum. Deterministic global optimizers such as Branch and Bound algorithms [8], however, do guarantee convergence to the global optima, yet the use of such algorithms becomes computationally prohibitive for multimodal acquisition functions. Recent advances in GP optimization [9] have made global optimization of GPs more accessible. Although related work theorizes about the potential benefits [10] of such approaches, their practical implementation remains largely unexplored. By utilizing this optimization approach for our framework, we aim to further advance the development of practical global optimization for multi-fidelity GPs. We propose to leverage the open-source deterministic solver MAiNGO (McCormick-based Algorithm for mixed-integer Nonlinear Global Optimization) [12] which employs a reduced-space formulation. Augmented to exploit parallel computing capabilities, MAiNGO becomes a practical choice to better optimize multi-fidelity GP acquisition functions.

We aim to benchmark our multi-fidelity optimization framework over a suite of optimization problems, including (a) enzymatic reaction networks [11] where the Quasi Steady State Approximation produces a low-fidelity model that is lower-dimensional but remains accurate only within limited parameter regimes; and (b) a programmable ammonia catalysis model [1], where varying computational accuracy (and thus speed) creates two distinct fidelity models. By emphasizing the constructive interaction between the levels of fidelity, facilitated by multi-fidelity GP, we aim to demonstrate the potential of our framework in optimizing expensive functions and advancing multi-fidelity optimization algorithms. Simultaneously, we utilize our approach for state-of-the-art dynamic catalysis to enhance production of ammonia, a key component in the drive towards renewable energy.

References

[1] G. R. Wittreich, S. Liu, P. J. Dauenhauer, and D. G. Vlachos. Catalytic resonance of ammonia

synthesis by simulated dynamic ruthenium crystal strain. Science Advances, 8(4):eabl6576, 2022.

[2] S. Guth, B. Champenois, and T. P. Sapsis. Application of gaussian process multi-fidelity optimal sampling to ship structural modeling. 2022.

[3] S. Guth and T. P. Sapsis. Wave episode based gaussian process regression for extreme event statistics in ship dynamics: Between the scylla of karhunen–loève convergence and the charybdis of transient features. Ocean Engineering, 266:112633, 2022.

[4] T. Savage, N. Basha, J. McDonough, O. K. Matar, and E. A. del Rio Chanona. Multi-fidelity

data-driven design and analysis of reactor and tube simulations. Computers Chemical Engineering,

179:108410, 2023.

[5] B. Shahriari, K. Swersky, Z. Wang, R. P. Adams, and N. de Freitas. Taking the human out of the loop: A review of bayesian optimization. Proceedings of the IEEE, 104(1):148–175, 2016.

[6] M. C. Kennedy and A. O’Hagan. Predicting the output from a complex computer code when fast approximations are available. Biometrika, 87(1):1–13, 2000.

[7] L. Le Gratiet and J. Garnier. Recursive co-kriging model for Design of Computer experiments with multiple levels of fidelity. International Journal for Uncertainty Quantification, 4(5):365–386, 2014.

[8] K. Kandasamy, G. Dasarathy, and B. Póczos. Multi-fidelity gaussian process bandit optimisation. Journal of Artificial Intelligence Research, 66:151–196, 2019.

[9] A. M. Schweidtmann, D. Bongartz, D. Grothe, T. Kerkenhoff, X. Lin, J. Najman, and A. Mitsos.Deterministic global optimization with gaussian processes embedded. Mathematical Programming Computation, 13(3):553–581, 2021.

[10] J. T. Wilson, F. Hutter, and M. P. Deisenroth. Maximizing acquisition functions for bayesian optimization. In Advances in Neural Information Processing Systems, volume 31, pages 9906–9917, 2018.

[11] N. Evangelou, N. J. Wichrowski, G. A. Kevrekidis, F. Dietrich, M. Kooshkbaghi, S. McFann, and I. G. Kevrekidis. On the parameter combinations that matter and on those that do not: data-driven studies of parameter (non)identifiability. PNAS Nexus, 1(4):pgac154, 09 2022.

[12] D. Bongartz, J. Najman, S. Sass, and A. Mitsos, “MAiNGO - McCormick-based Algorithm for mixed-integer Nonlinear Global Optimization,” 2018. accessed 2023/07/20.