(125a) Multi Agent Reinforcement Learning and Graph Neural Networks for Inventory Management

Classic methods to solve the inventory control problem involve heuristics such as the (s,S) and (r,Q) policy [1, 2]. These heuristics are traditionally used due to the ease of their implementation but lack adaptability to changing demand patterns and coordination amongst different entities leading to sub-optimal performance [2]. Another common method involves dynamic programming, a mathematical optimization technique which solves complex problems by breaking them down into small subproblems. This offers a more robust solution but becomes computationally infeasible for complex systems due to the curse of dimensionality. Reinforcement learning (RL) offers a promising alternative approach by combining the strengths of dynamic programming and heuristics, offering an approximate dynamic programming solution [3]. This allows RL to adapt better to changing demand patterns and uncertainties in the supply chain, enhancing decision-making in supply chains. However, as the supply chain grows in size, traditional RL, and Linear Programming (LP) methods may struggle due to the increased complexity and computational requirements. Moreover, both LP and RL can provide optimal solutions but require full online information about the system, which may not always be feasible or practical in real-world scenarios when information sharing constraints are present.

2. Methodology

MARL and GNN Framework for Supply Chain Optimization

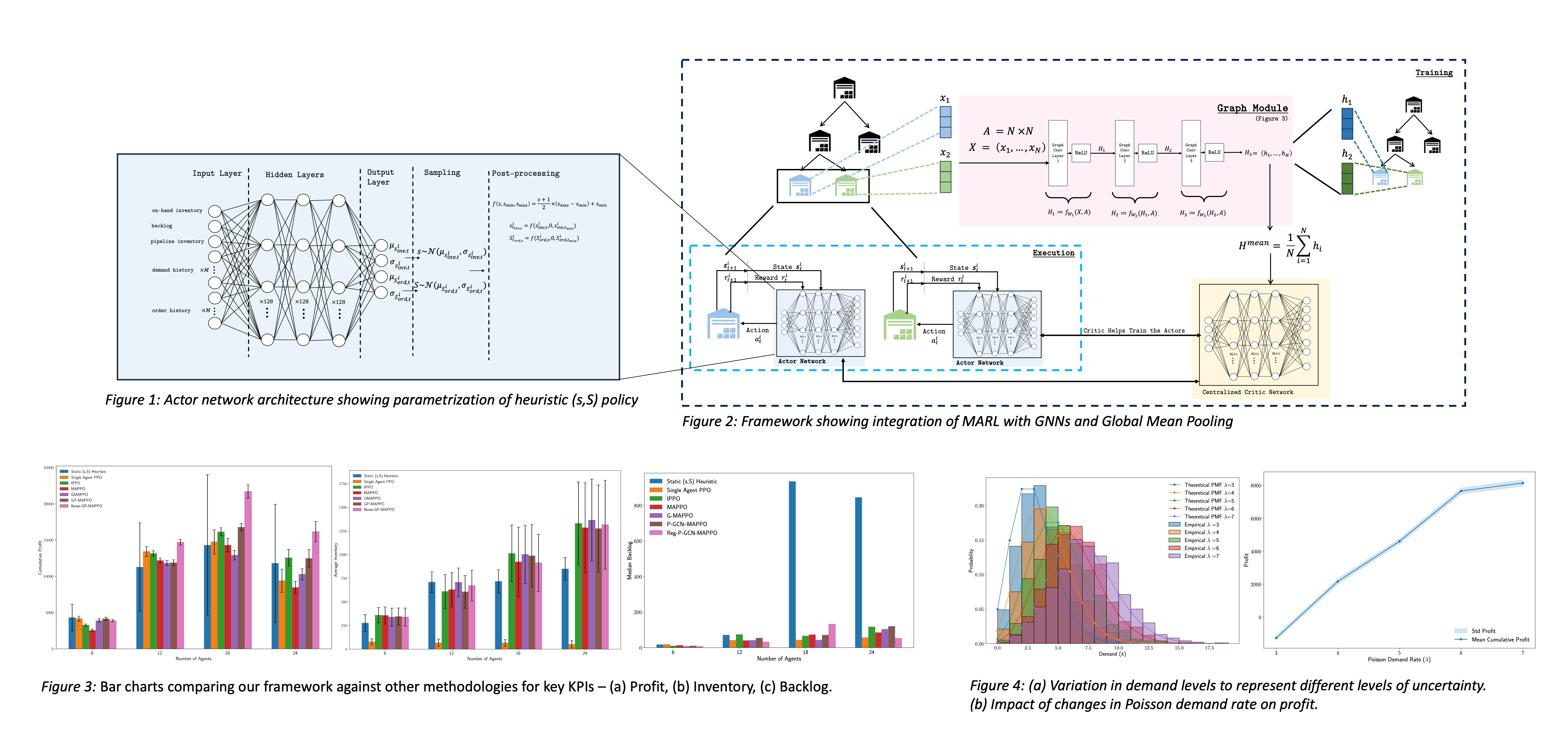
To overcome these limitations, we propose a multi-agent reinforcement learning (MARL) framework enhanced with Graph Neural Networks (GNNs) for multi-echelon inventory management. MARL operates in a distributed decision-making framework, allowing agents to make decisions based on local observations and interactions, improving scalability and coordination in large-scale supply chains. Our framework follows the Centralized Training, Decentralized Execution (CTDE) paradigm, where central state information is shared offline during training, while only local state information is required during online execution. Additionally, to capture the inherent structure of supply chains, we model the supply chain as a graph, where nodes represent individual entities (such as retailers, warehouses, or suppliers) and edges capture interactions such as inventory flow. GNNs leverage this graph structure to aggregate information from neighboring nodes, capturing hidden interdependencies that are critical for improving coordination and decision-making in multi-agent systems. This aggregated information is then used to train the critic, enhancing policy learning and guiding more effective and collaborative inventory strategies.

We introduce two versions of our framework: (1) a GNN-critic approach, where the aggregated vector from the GNN trains the critic, improving policy learning through hidden interdependencies, and (2) a global mean pooling framework that aggregates vectors from the GNN hence reducing dimensionality and computational complexity without compromising performance as shown in Figure 2. Both frameworks leverage the supply chain's structure to learn hidden interdependencies, enhancing communication and coordination between entities for improved decision-making in the multi-agent system.

Action Space Redefinition

While the MARL+GNN framework addresses scalability and coordination challenges, RL often struggles with integer or mixed-integer decisions, which are common in inventory management problems (e.g., order quantities). As the scale of inventory systems increases, the complexity of the decision-making process grows, resulting in a significantly larger action space. This increased complexity can hinder the effectiveness of RL algorithms, requiring extensive training data and longer convergence times to identify optimal policies.

To mitigate these challenges, we redefine the action space to parametrize a heuristic (s, S) policy, as shown in Figure 1, enhancing adaptability, practicality, and explainability for real-world implementation. Rather than directly predicting order replenishment quantities, which can be difficult to scale, we model the action space as continuous in the range [-1, 1], allowing the policy to dynamically adjust the reorder point (s) and order-up-to level (S). By treating these parameters as stochastic variables drawn from Gaussian distributions, our approach adapts more effectively to fluctuations in demand and lead-time uncertainties, improving performance across various supply chain configurations.

3. Results and Discussion

We evaluate our framework across four supply chain configurations, ranging from 6 to 24 nodes, and compare its performance against the heuristic (s, S) policy, single-agent RL, and two multi-agent RL baselines — IPPO (Independent Proximal Policy Optimization) and MAPPO (Multi Agent Proximal Policy Optimization). Our evaluation focuses on key KPIs such as profit, backlog, and on-hand inventory as shown in Figure 3. The results demonstrate that graph-based methods consistently outperform traditional approaches, with the GNN framework using global mean pooling and regularization achieving the best results. This framework balances computational efficiency with optimal decision-making by leveraging global mean pooling to reduce dimensionality and applying regularization to prevent overfitting, ensuring robust performance across diverse supply chain environments. Additionally, we perform an uncertainty analysis by varying the level of uncertainty in demand to assess the robustness of the policies as shown in Figure 4. We observe that the standard deviation of profit remains relatively unchanged, indicating that the policies are robust to fluctuations in demand.

4. Conclusions

This work presents a MARL framework enhanced with GNNs for multi-echelon inventory management, addressing scalability and coordination challenges in large-scale supply chains. By modeling the supply chain as a graph, our approach captures critical interdependencies between entities, improving decision-making across diverse environments. We redefine the action space to parametrize a heuristic (s, S) policy, enabling dynamic adjustments of reorder points and order-up-to levels. Our results show that graph-based methods consistently outperform traditional approaches, with the GNN framework using global mean pooling and regularization achieving the best performance. Future work will explore the integration of attention networks to assign varying importance to neighboring nodes, allowing the framework to retain more local, spatial information. We plan to extend the approach to more complex systems involving a larger number of products and non-stationary demand, better mimicking real-world supply chain conditions and further improving the scalability and adaptability of the model.

The full paper is available at https://arxiv.org/abs/2410.18631 and the codes are available at https://github.com/OptiMaL-PSE-Lab/MultiAgentRL_InventoryControl.

[1] Jackson, I., Tolujevs, J. and Kegenbekov, Z., 2020. Review of inventory control models: a classification based on methods of obtaining optimal control parameters. Transport and Telecommunication, 21(3), pp.191-202.

[2] Brunaud, B., Laínez‐Aguirre, J.M., Pinto, J.M. and Grossmann, I.E., 2019. Inventory policies and safety stock optimization for supply chain planning. AIChE journal, 65(1), pp.99-112.

[3] Hubbs, C.D., Li, C., Sahinidis, N.V., Grossmann, I.E. and Wassick, J.M., 2020. A deep reinforcement learning approach for chemical production scheduling. Computers & Chemical Engineering, 141, p.106982.

[4] Daoutidis, P., Allman, A., Khatib, S., Moharir, M.A., Palys, M.J., Pourkargar, D.B. and Tang, W., 2019. Distributed decision making for intensified process systems. Current Opinion in Chemical Engineering, 25, pp.75-81.

[5] Sarkis, M., Bernardi, A., Shah, N. and Papathanasiou, M.M., 2021. Decision support tools for next-generation vaccines and advanced therapy medicinal products: present and future. Current Opinion in Chemical Engineering, 32, p.100689.

[6] Mousa, M., van de Berg, D., Kotecha, N., del Rio-Chanona, E.A. and Mowbray, M., 2023. An Analysis of Multi-Agent Reinforcement Learning for Decentralized Inventory Control Systems. arXiv preprint arXiv:2307.11432.

[7] Liu, X., Hu, M., Peng, Y. and Yang, Y., 2022. Multi-Agent Deep Reinforcement Learning for Multi-Echelon Inventory Management. Available at SSRN.