(679b) Mpax: Mathematical Programming in Jax

Mathematical programming is a cornerstone of process system engineering, underpinning critical applications such as process control, production scheduling, supply chain optimization and process synthesis^1,2. While modern solvers like GUROBI, IPOPT³ and BARON⁴ have achieved strong performance and reliability, they remain fundamentally constrained by traditional CPU-based solution paradigms. Core algorithms such as the simplex and interior-point methods rely on solving large linear systems using direct methods like Cholesky factorization. These computations are inherently sequential and thus difficult to parallelize, which in turn limits the scalability of solvers to shared-memory, CPU-based architectures. As problem sizes grow, these limitations lead to increasing memory bottlenecks and reduced computational efficiency.

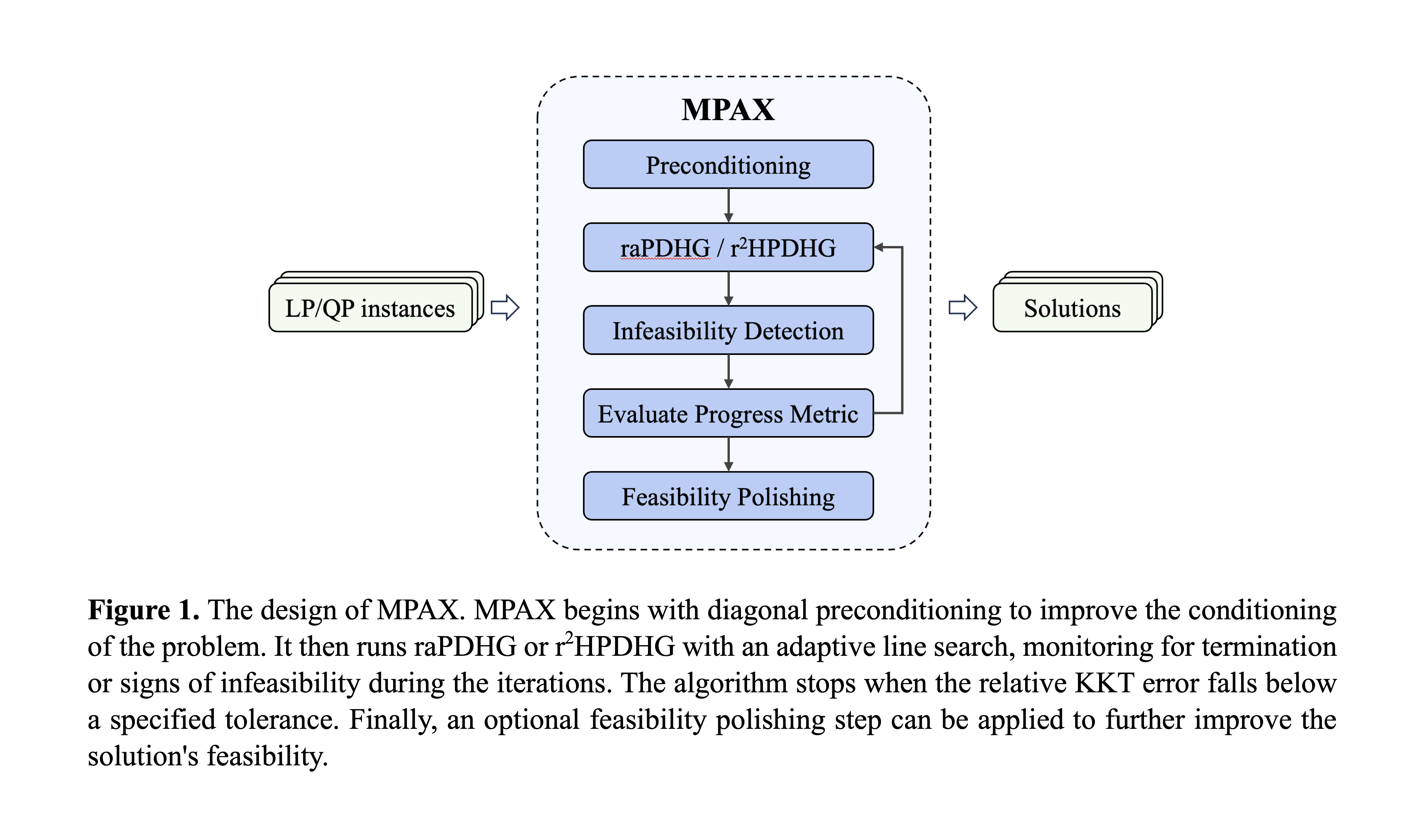
To address these challenges, this work presents MPAX (Mathematical Programming in JAX), a versatile and efficient solver designed for modern hardware. MPAX is built on two key pillars: recent advancements in first-order methods for solving mathematical programming problems, and the rapid progress of modern programming languages on contemporary computational platforms. From an algorithmic perspective, MPAX has implemented the state-of-the-art first-order methods, restarted average primal-dual hybrid gradient^5,6 and reflected restarted Halpern primal-dual hybrid gradient⁷ methods, whose primary computational bottleneck is merely matrix-vector multiplication. Currently, MPAX supports both linear programming and quadratic programming. Future developments will extend it capability to more general mathematical programming problems and specialized modules. Implemented in JAX, MPAX offers a unified and high-performance framework with several valuable features, including native support for CPUs, GPUs, and TPUs, batched solving of multiple instances, auto-differentiation, and efficient device parallelism. More importantly, it enables the seamless integration with machine learning pipelines, simplifying downstream applications and enhancing both flexibility and performance. Extensive numerical experiments demonstrate the advantages of MPAX over existing solvers. The solver is available at https://github.com/MIT-Lu-Lab/MPAX.

Reference:

[1] Grossmann, I. (2005). Enterprise‐wide optimization: A new frontier in process systems engineering. AIChE Journal, 51(7), 1846-1857.

[2] Grossmann, I. E. (2012). Advances in mathematical programming models for enterprise-wide optimization. Computers & Chemical Engineering, 47, 2-18.

[3] Wächter, A., & Biegler, L. T. (2006). On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Mathematical programming, 106, 25-57.

[4] Tawarmalani, M., & Sahinidis, N. V. (2005). A polyhedral branch-and-cut approach to global optimization. Mathematical programming, 103(2), 225-249.

[5] Applegate, D., Díaz, M., Hinder, O., Lu, H., Lubin, M., O'Donoghue, B., & Schudy, W. (2021). Practical large-scale linear programming using primal-dual hybrid gradient. Advances in Neural Information Processing Systems, 34, 20243-20257.

[6] Lu, H., & Yang, J. (2023). cuPDLP. jl: A GPU implementation of restarted primal-dual hybrid gradient for linear programming in Julia. arXiv preprint arXiv:2311.12180.

[7] Lu, H., & Yang, J. (2024). Restarted Halpern PDHG for linear programming. arXiv preprint arXiv:2407.16144.