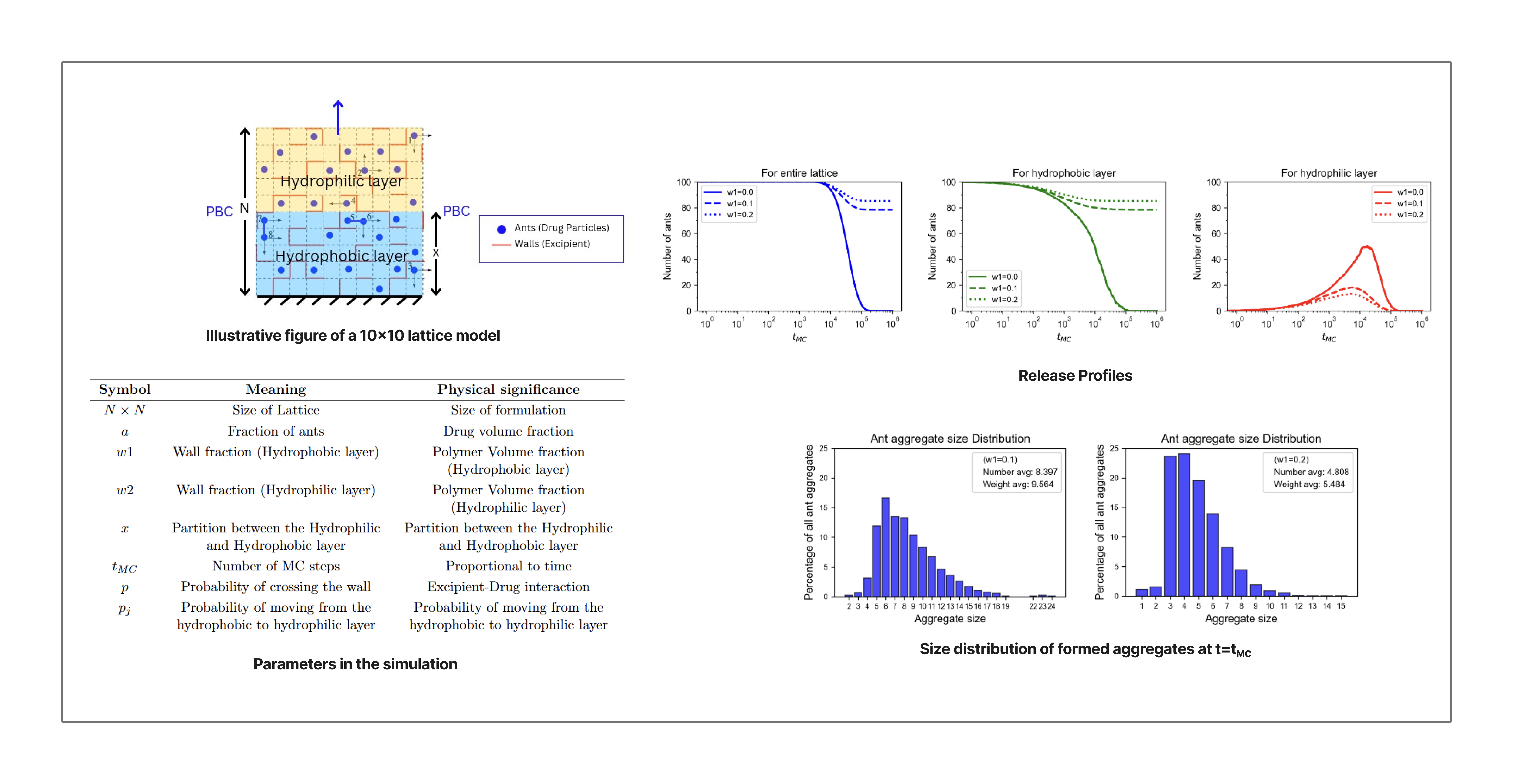
Pharmaceutical Drug Delivery Systems are typically comprised of a drug and an excipient that facilitates drug delivery. Polymeric excipients are usually employed in controlled release formulations to control the duration and rate of drug release. While various mass transport mechanisms such as dissolution, swelling, and erosion contribute to drug release, our work focuses on modelling systems where diffusion is the governing mechanism. Mechanistic modelling of the process via mathematical equations is challenging due to the complexity of drug release phenomena. Empirical models such as the Higuchi Law, Power Law, and Weibull function, although simple to use, are not exactly based on the actual description of the physical processes involved and thus cannot reliably predict release profiles for new formulations. To deal with these challenges, Monte Carlo (MC) techniques have been utilized to simulate various complex systems, based on the idea that drug diffusion is a stochastic process. In our work, we consider Mesoscale Lattice-based models to study diffusion-driven drug release phenomena from the polymer matrix. The core idea is that the drug particles are essentially performing a “random walk” inside the polymer matrix. Thus, for the sake of simplicity, our model uses the analogy of ants performing a random walk on a two-dimensional maze, where the ants and maze represent the drug and excipient molecules, respectively. The lattice is a composite membrane consisting of two layers: a hydrophobic thin film where ants (drug particles) form aggregates or crystals if they are present in adjacent cells and thus move together, and a hydrophilic thin film where they do not. The diffusion process is simulated by selecting an ant or ant aggregate at random and allowing it to move to an adjacent cell in any of the four directions based on a random number generation process. Polymeric excipients are present as walls (cell boundaries) between the cells, restricting the free movement of ants by randomly rejecting the attempts of ants to move to an adjacent cell. A number of physically relevant and controllable parameters are present in our simulation, such as the size of the lattice, number of MC steps, polymer loading, drug loading, excipient-drug interactions, and thickness of the hydrophobic and hydrophilic layers, which are varied to obtain results from different studies conducted in our work. The lattice-based model provides us with a qualitative understanding of the diffusion-driven transport phenomena, which will prove useful in designing controlled release formulations. Future work would entail including other release mechanisms such as dissolution, erosion, and swelling of the matrix in the simulation.
