(203e) Minimally Empirical, Interpretable Interatomic Potentials for Atomistic Simulations of Rare-Earth Electroseparations

The widespread use of rare-earth elements (REEs) and platinum-group metals (PGMs) in modern technologies, from computers to phones, coupled with their limited reserves, places significant demands on current recovery methods. Traditionally employed separations methods suffer from poor selectivity (for example due to element’s dilute concentration), are irreversible, and generate substantial waste. Electrosorption processes utilizing redox-active electrodes have emerged as a promising alternative to address these limitations. However, optimizing these electrodes for REE separations requires understanding of their interaction with solvated species. Current theoretical approaches are either computationally slow (DFT) or lack necessary quantum-mechanical features such as charge-transfer (force-fields).

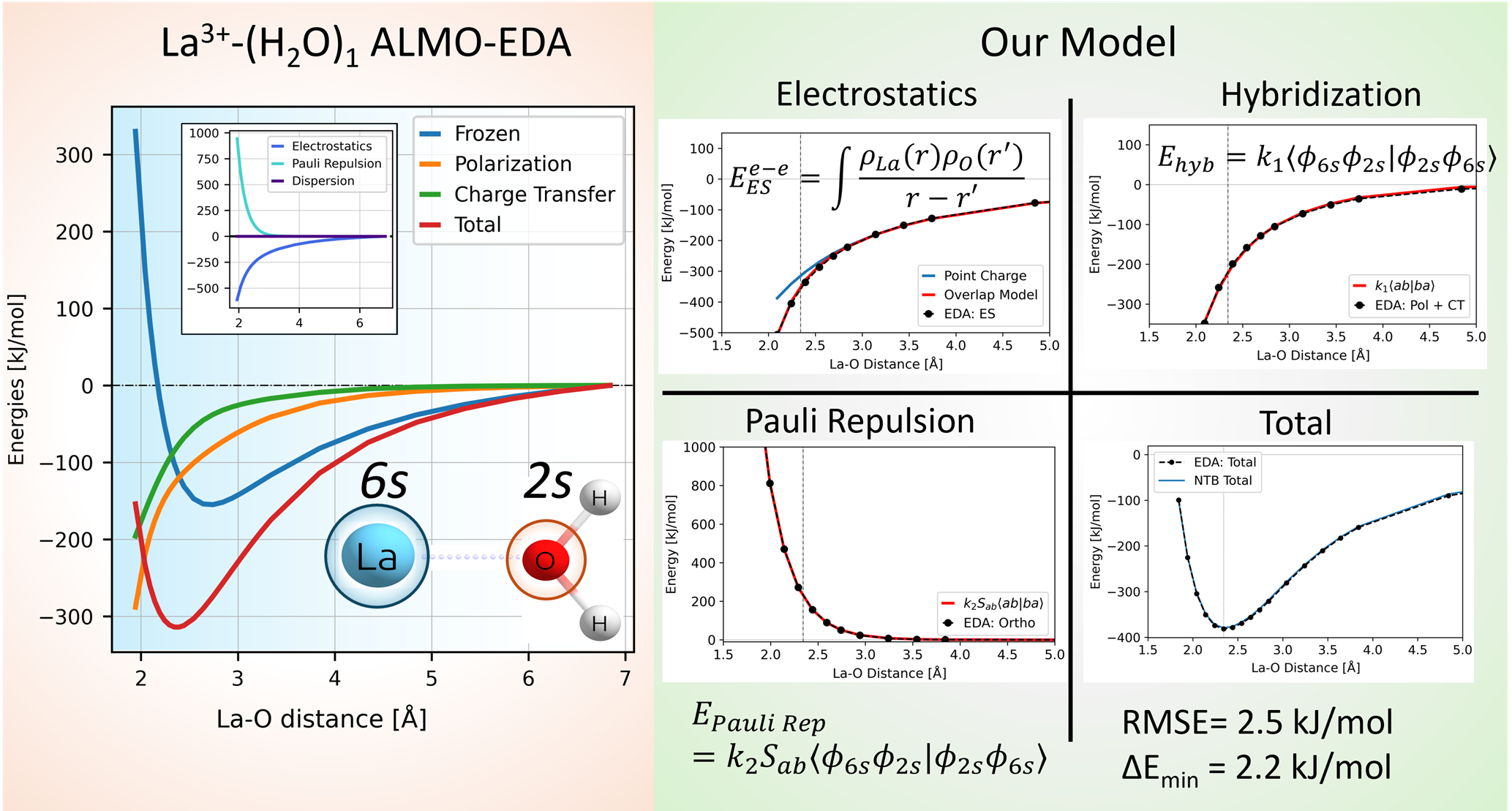
To facilitate long-timescale molecular dynamics calculations, in this work, we are developing a minimally empirical tight-binding theory for aqueous La³⁺ system. We are fitting physically motivated functional forms to energy contributions obtained from ALMO-EDA (HF-D3BJ/def2-ma-TZVP). For example, to describe permanent electrostatics, we use an atomic orbital overlap dependence attaining high accuracy with minimal changes to orbital exponents. We combine polarization and charge transfer energies to describe hybridization as k<ab|ba>, an expression quantum-mechanical feature. Finally, we model the Pauli repulsion as the product of overlap and the earlier <ab|ba> expression. Our preliminary work on La³⁺-(H₂O) shows excellent performance requiring only a few parameters and only O(10) data points. The simplicity of the functional forms ensures potential transferability to a more complex solvation environments.

By avoiding calculation of expensive 2-electron integrals, our method achieves 500x speedup compared to ALMO-EDA with very little compromise on accuracy. Its fast performance and the limited number of parameters suggests transferability of the model framework for other promising applications such as catalysis.