2025 AIChE Annual Meeting
(308a) Membrane System Synthesis for Critical Metal Recovery
Recent research has explored membrane-based technologies for recovering critical metals from wastewater. These technologies utilize semi-permeable membranes to selectively separate metal ions based on their physicochemical properties and offer significant advantages, including low energy consumption, chemical-free operation, and minimal secondary waste generation [3]. Membrane-based technologies are generally classified into four primary categories: microfiltration (MF), ultrafiltration (UF), nanofiltration (NF), and reverse osmosis (RO). Among these, NF membranes have proven particularly effective for recovering critical metals from wastewater, as their intermediate pore size – between UF and RO – enables selective and efficient separation of metal ions. Commercially available NF membranes are synthetic thin-film polymer composites containing charged functional groups, enhancing their ability to separate metal ions. However, polymeric NF membranes inherently exhibit a trade-off between selectivity and permeability [4]. Therefore, recent research has focused on developing novel polymeric materials with enhanced transport properties to achieve a more efficient recovery of critical metals. Nevertheless, many commercially available membranes still demonstrate the inherent selectivity-permeability tradeoff, posing a major challenge for separations requiring simultaneous high purity and recovery.
To overcome this challenge, multiple NF membranes with distinct material properties – such as solvent flux, metal rejection coefficient, and transmembrane pressure gradients – can be interconnected to form a membrane network. Optimization-based methods are often employed for membrane network synthesis across various applications [5–7]. Accordingly, we present an optimization framework for synthesizing membrane networks to recover multiple critical metals from industrial wastewater. This framework encompasses three key elements: (1) a membrane unit model, (2) a comprehensive membrane network superstructure, and (3) a mixed-integer nonlinear programming (MINLP) model.
We introduce a transport model, the Spiegler-Kedem-Katchalsky (SKK) model, to characterize the permeation of metallic ions through an NF membrane by integrating both diffusive and convective mechanisms [8]. Although initially introduced for reverse osmosis applications, subsequent studies have demonstrated its applicability for nanofiltration [9,10]. The SKK model establishes a relationship between the volumetric solvent flux, solute fluxes, local solute concentrations, and membrane material properties. Subsequently, we develop a nonlinear algebraic membrane unit model that builds upon the SKK model to determine both the permeate and retentate flowrates and the required membrane area for a specific separation task.
We propose a superstructure with extensive interconnections, designed to recover multiple target metals from wastewater. The superstructure consists of several interlinked trains, each specifically tailored to recover one target metal. Each train comprises multiple interconnected stages that employ distinct membrane materials, selectively chosen for efficient recovery of the assigned target metal. Within each train, retentate/permeate stream can be: (1) bypassed to the next two stages (bypass stream), (2) recycled to the current and previous stage (recycle stream), or (3) collected as the product (product stream). The fresh feed can enter any train, where a portion undergoes the desired separation, while the remainder may bypass the train entirely and be collected in the final retentate/permeate product. The final retentate product from each train contains the target metal specific to that train, while the final permeate product (residual) is fed to subsequent trains for further separation of the remaining target metals. Further, to limit the number of symmetrical solutions, the fresh feed is constrained to enter only the first stage of a train.
Subsequently, we formulate a mixed-integer nonlinear programming (MINLP) model, which incorporates both binary and continuous variables to represent configurational and operational decisions, respectively. This MINLP model is then solved to simultaneously determine the optimal membrane materials for each stage, the optimal network configuration, and operating conditions that minimize the total annualized operating cost of the membrane network.
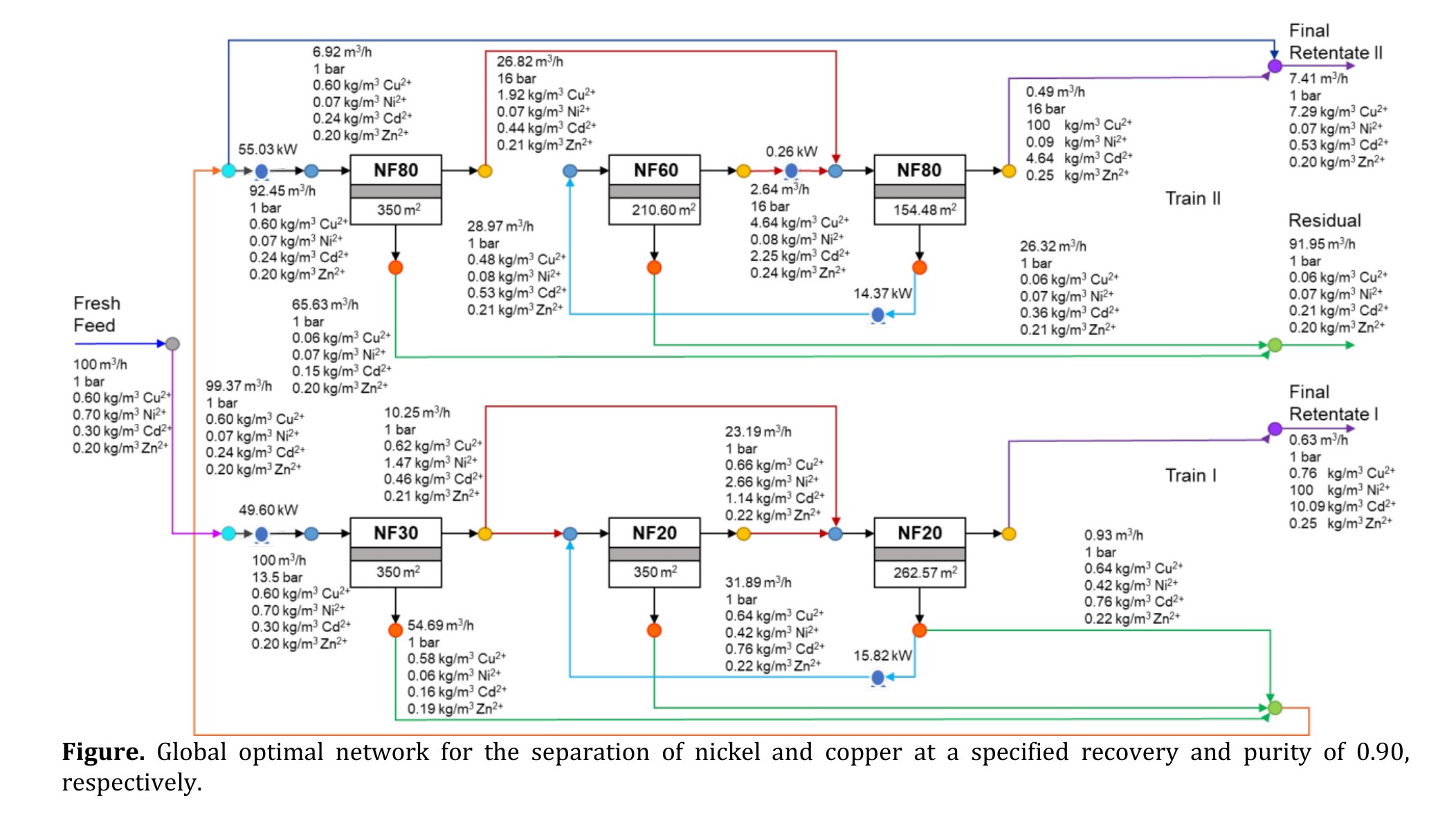
Finally, we demonstrate the effectiveness of the proposed framework in achieving globally optimal solutions through various case studies. First, we synthesize a one-train network utilizing a unique material for the separation and recovery of lithium from an aqueous solution of spent lithium-ion batteries. Additionally, we conduct sensitivity analysis on recovery and purity specifications to study their impact on the network’s operational and economic performance. Second, we present the membrane network synthesis for the separation and recovery of nickel and copper from wastewater generated by electroplating industries, permitting the selection of distinct materials from the available potential materials for each stage; the optimal network is illustrated in the given figure. Third, we demonstrate how the proposed framework can be extended to multiple trains for the simultaneous recovery of multiple target metals. Specifically, we present the synthesis of four-train network to simultaneously recover four target metals from wastewater generated by mining industries.
References
[1] R.G. Eggert, Critical Minerals and Emerging Technologies, Issues Sci. Technol. 26 (2010) 49–58.
[2] A.G. Chmielewski, T.S. Urbański, W. Migdał, Separation technologies for metals recovery from industrial wastes, Hydrometallurgy 45 (1997) 333–344. https://doi.org/10.1016/S0304-386X(96)00090-4.
[3] H. Strathmann, Membrane separation processes, J. Membr. Sci. 9 (1981) 121–189. https://doi.org/10.1016/S0376-7388(00)85121-2.
[4] L.M. Robeson, The upper bound revisited, J. Membr. Sci. 320 (2008) 390–400. https://doi.org/10.1016/j.memsci.2008.04.030.
[5] H. Verma, D. Jassby, C.T. Maravelias, Superstructure-based optimization of membrane network systems for multicomponent liquid mixture separation, J. Membr. Sci. 717 (2025) 123574. https://doi.org/10.1016/j.memsci.2024.123574.
[6] Z. Chen, M. Tawarmalani, R. Agrawal, Global minimization of power consumptions for multicomponent gas membrane cascades, Comput. Chem. Eng. 180 (2024) 108464. https://doi.org/10.1016/j.compchemeng.2023.108464.
[7] R.V.S. Uppaluri, P. Linke, A.C. Kokossis, Synthesis and Optimization of Gas Permeation Membrane Networks, Ind. Eng. Chem. Res. 43 (2004) 4305–4322. https://doi.org/10.1021/ie030787c.
[8] K.S. Spiegler, O. Kedem, Thermodynamics of hyperfiltration (reverse osmosis): criteria for efficient membranes, Desalination 1 (1966) 311–326. https://doi.org/10.1016/S0011-9164(00)80018-1.
[9] R.B. Merlet, C.R. Tanardi, I.F.J. Vankelecom, A. Nijmeijer, L. Winnubst, Interpreting rejection in SRNF across grafted ceramic membranes through the Spiegler-Kedem model, J. Membr. Sci. 525 (2017) 359–367. https://doi.org/10.1016/j.memsci.2016.12.013.
[10] Y. Zhang, L. Zhang, L. Hou, S. Kuang, A. Yu, Modeling of the variations of permeate flux, concentration polarization, and solute rejection in nanofiltration system, AIChE J. 65 (2019) 1076–1087. https://doi.org/10.1002/aic.16475.