(696c) Limiting Laws for Charge Transport in Isotropic Systems of Conjugated Polymers

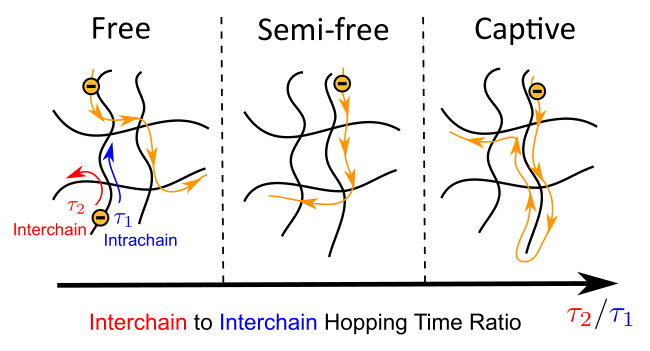
Alternating single and double bonds in the backbone of conjugated polymers provide them with electrical conductivity. This work models charge transport within these polymers as a diffusion process involving two distinct mechanisms: intrachain and interchain hopping, characterized by the time scales τ₁ and τ₂, respectively. We calculate the diffusivity of charge carriers in isotropic melts and semidilute solutions of conjugated polymers under weak electric fields. By extending the approach initially proposed by de Gennes [Phys. A: Stat. Mech. Appl. 1986] and later re-introduced by the other authors, we identify three universal charge transport regimes: free, semi-free, and captive. In the free regime, rapid interchain hopping results in a diffusivity independent of polymer chain length, D_free ∼ τ₁^-1N⁰. In the semi-free regime, slower interchain hopping relative to intrachain hopping makes diffusivity dependent on both time scales, D_semi-free ∼ τ₁^-1/2τ₂^-1/2N⁰. Finally, in the captive regime, significantly restricted interchain hopping leads to charge carrier traversing the entire polymer chain before hopping to the next one, resulting in diffusivity linearly proportional to the chain length, D_captive ∼ τ₂^-1N¹. These scaling relationships also extend from melts of flexible chains to semiflexible polymers and semidilute solutions, where the polymer volume fraction influences the pairwise contact probability. Weakly and strongly fluctuating solutions are analyzed using mean-field and scaling approaches, respectively. The charge hopping approach is demonstrated to be equivalent to consideration of the systems as a finite resistor ladder. Charge carrier diffusivity and resulting conductivity are also found for AC as functions of frequency. Our results provide fundamental insights that could inform the design of polymer-based flexible and stretchable electronics.