(204h) Koopman-Nemytskii Operator: A Linear Representation of Nonlinear Controlled Systems

Linearization is a common and natural idea of handling the nonlinearity of process dynamics. A recent trend in the studies of nonlinear dynamics and control is the use of operator-theoretic methods, especially Koopman operators, to provide a globally linear representation of nonlinear systems [1]. For an autonomous system in discrete time with transition map f, the Koopman operator is defined as the mapping any observable g (on a function space) to its composition with f, namely g ⸰ f. Although such a Koopman operator is infinite-rank, its linearity is beneficial for solving control-theoretic problems. In fact, given a sample of snapshots as the data, the Koopman operator can be conveniently approximated as a finite-rank one; a popular approach for Koopman operator learning is known as extended dynamic mode decomposition (EDMD) [2], which seeks a matrix on the span of dictionary functions. Remarkably, the EDMD can be extended into a kernel version, using the theory of reproducing kernel Hilbert spaces (RKHSs). In particular, under mild regularity conditions on the dynamics, the Koopman operator is well-posed as a linear bounded operator on a Sobolev-Hilbert space [3], which coincides with the RKHS when a compactly supported function is adopted as the radial basis function defining the kernel [4].

For non-autonomous systems with inputs, the definition of Koopman operator needs to be extended to account for the effect of inputs on the dynamics. Existing approaches typically consider the dependence of Koopman operator on open-loop input values. Considering continuous-time systems where the dynamics is input-affine, the generator of Koopman semigroup (namely the Lie operator) is a linear combination of multiple operators with input values being the coefficients; more generally, the Koopman operator can be regarded as an interpolation among input values [5–7]. In empirical studies, it is typically assumed that the input-related terms are (approximately) in the span of Koopman eigenfunctions and thus the non-autonomous system becomes a finite-dimensional bilinear one (e.g., [8]). When the bilinear form is not exact, the controller synthesis in the presence of this mismatch is recently considered in [9].

From a controller design (closed-loop) point-of-view, it is desirable to consider the dependence of Koopman operator on the feedback laws (i.e., feedback policies). That is, by considering a certain class of feedback policies (instead of a certain set of input values) and the resulting properties of the system around a fixed equilibrium point, one can design the feedback law to achieve desired stability and performance metrics. Essentially, the closed-loop prediction of states and control cost is the capability in need. Therefore, in this work, to represent any nonlinear controlled dynamics in a linear manner, a new operator termed Koopman-Nemytskii operator is proposed.

• Under regularity conditions, it is established that the Koopman operator K, which is properly defined from an RKHS of states to an RKHS of states, continuously depend on the feedback policy. Hence, the adjoint operator of the Koopman operator K* is also continuously mapped from the policy space u ∈ U. The K* satisfy the property of mapping the canonical feature of states to succeeding states:

K*(ϕ(x)) = ϕ(x⁺).

• By defining a RKHS on the policy space, i.e., by assigning a kernel function of any pair of feedback policies, the afore-mentioned continuous mapping from u to K* is lifted to a mapping from this policy-based RKHS. Using isomorphism arguments, we define the Koopman-Nemytskii operator T as the transform that maps the canonical feature of states and the canonical feature of policy to that of the succeeding states:

T(ϕ(x), φ(u)) = ϕ(x⁺).

The Koopman-Nemytskii operator proposed here is generic and exact, not restricted to input-affine systems and applicable to all smooth enough and non-degenerate dynamics in discrete time. The extension to continuous time is also natural by replacing the Koopman operator with the infinitesimal generator of the Koopman semigroup.

Then, given a finite sample of state-policy-successor snapshots, the Koopman-Nemytskii operator can be finite-rank approximated from data using the kernel EDMD approach. The following types of theoretical properties are established for the data-driven estimation: (i) generalized error for predicting the states in a single time step, (ii) multi-step state prediction error up to any time t, and (iii) the error of calculating the cost incurred by the feedback policy u, where the stage cost terms are expressed as quadratic forms of canonical features on the RKHSs. The obtained errors under kernel EDMD is uniform over the initial states and policies, dependent on the fill distance of data points in the state and policy spaces. Two realistic process control examples – (i) liquid tank regulated a nonlinear valve and (ii) the William-Otto reactor, are used to demonstrate the practical performance.

Remark

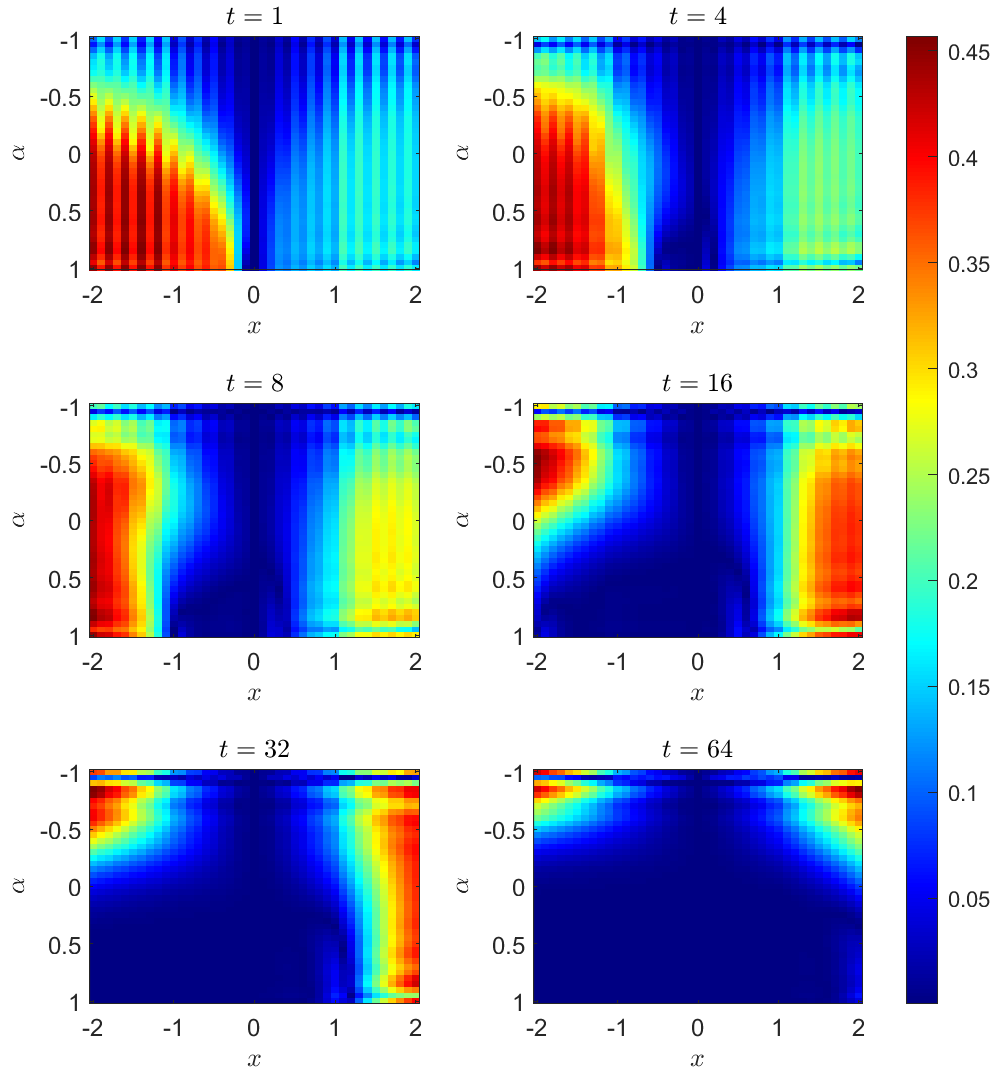
The figure appended illustrates the state prediction error of the tank-valve example (starting from initial state x under controller parameters α) and as time t proceeds.

References

1. S. L. Brunton, M. Budišić, E. Kaiser, and J. N. Kutz, “Modern Koopman theory for dynamical systems,” SIAM Rev., vol. 64, no. 2, 229–340.
2. M. O. Williams, I. G. Kevrekidis, and C. W. Rowley, “A data-driven approximation of the Koopman operator: Extending dynamic mode decomposition,” J. Nonlin. Sci., vol. 25, pp. 1307–1346, 2015.
3. F. Köhne, F. M. Philipp, M. Schaller, A. Schiela, and K. Worthmann, “L∞-error bounds for approximations of the Koopman operator by kernel extended dynamic mode decomposition,” arXiv preprint, 2024, arXiv:2403.18809.
4. H. Wendland, Scattered data approximation. Cambridge University Press, 2004.
5. M. O. Williams, M. S. Hemati, S. T. M. Dawson, I. G. Kevrekidis, and C. W. Rowley, “Extending data-driven Koopman analysis to actuated systems,” IFAC-PapersOnLine, vol. 49, no. 18, pp. 704–709, 2016.
6. S. Peitz, S. E. Otto, and C. W. Rowley, “Data-driven model predictive control using interpolated Koopman generators,” SIAM J. Appl. Dyn. Syst., vol. 19, no. 3, pp. 2162–2193, 2020.
7. P. Bevanda, B. Driessen, L. C. Iacob, R. Toth, S. Sosnowski, and S. Hirche, “Nonparametric control-Koopman operator learning: Flexible and scalable models for prediction and control,” arXiv preprint, 2024, arXiv:2405.07312.
8. D. Bruder, X. Fu, R. B. Gillespie, C. D. Remy, and R. Vasudevan, “Data-driven control of soft robots using Koopman operator theory,” IEEE Trans. Robot., vol. 37, no. 3, pp. 948–961, 2020.
9. R. Strässer, M. Schaller, K. Worthmann, J. Berberich, and F. Allgöwer, “Koopman-based feedback design with stability guarantees,” IEEE Trans. Autom. Control, vol. 70, no. 1, pp. 355–370, 2025.