Batch process systems exhibit transient, potentially nonlinear dynamic behavior without an operating equilibrium point
1. For control of these processes, nonlinear model predictive control (NMPC) is a promising method to control constrained multi-input, multi-output (MIMO) systems
2. NMPC is particularly beneficial for batch polymerization processes, where strict process safety, quality requirements, and product consistency need to be met for each batch. However, the adoption of NMPC is hindered by the availability of accurate dynamic models
3, as the control method relies on these models to predict future state trajectories. Such models are often difficult and expensive to obtain via experiments and/or mechanistic knowledge. Considering that batch processes are used to produce small quantities of customized products, the cost of acquiring numerous models is generally not justified. As an alternative for scenarios of no prior knowledge of the system, we propose an iterative batch model identification scheme via Gaussian Process (GP) based NMPC (GP-NMPC) for batch processes. GP regression models have been employed to learn nonlinear discrete-time dynamics directly from available observations
4,5. Our approach includes NMPC applied to polymerization batches iteratively, with the GP models updated with new observations at the end of each batch. With increasing observations on the operating region, the GP state space model predicts more accurate trajectories, which in turn improves NMPC performance in each batch iteration. As the computational effort of GP inference scales with the data, we use K-means clustering to reduce the size of the inferred dataset. Often, closed-loop responses between iterations are similar, and certain operating regions become dense with repetitive data. Via K-means clustering, we select sparse data from each cluster, reducing computational effort. Since the GPs are only fitted on measured operational data, they yield high accuracy only around the optimal decisions and state trajectory, with convergence of the iterative scheme. Although the representation by the fitted GPs do not generalize to the whole domain, the iterative scheme presents a data efficient approach to obtaining GP models for optimal control. We apply the proposed learning scheme on a semi-batch polymerization reactor
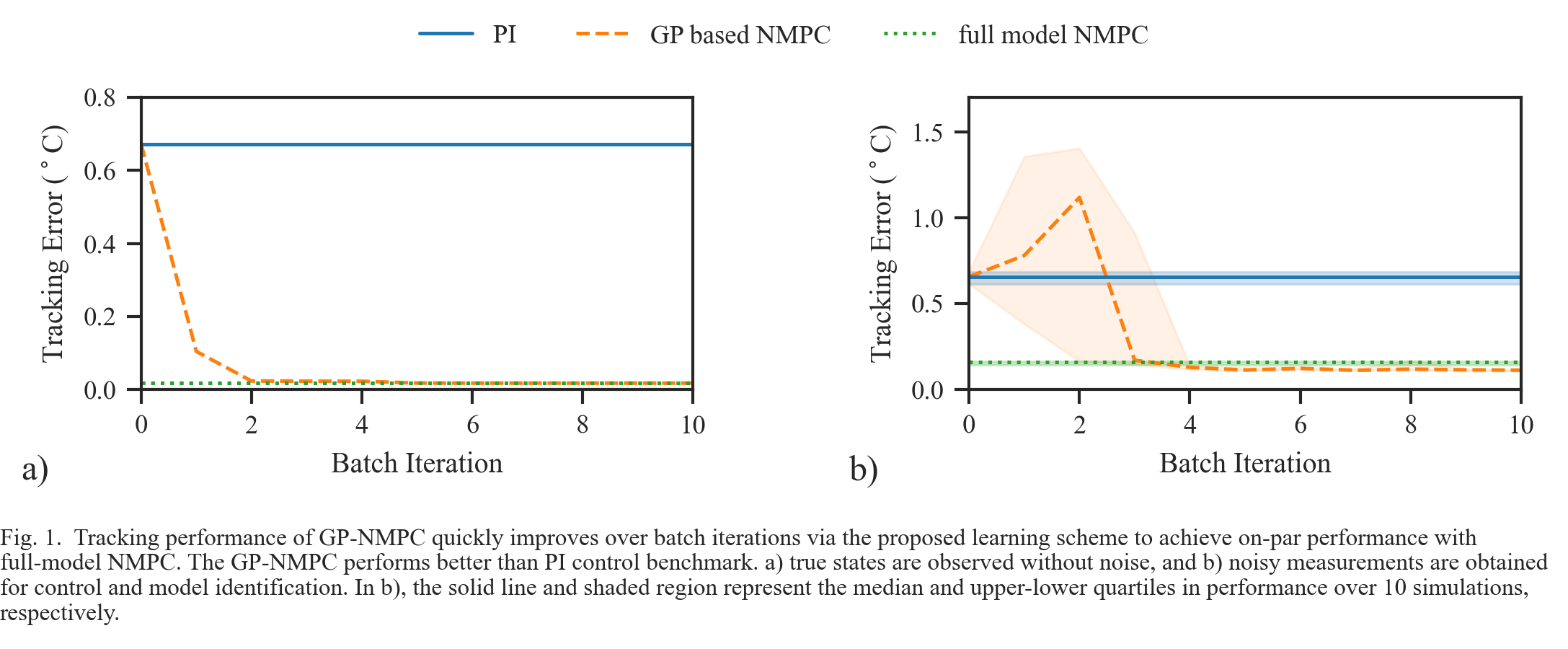
in silico to perform temperature setpoint control over batch durations of two hours, with tight quality constraint bounds ±2°C around the setpoint. A total of 10 iterations are performed to observe changes in tracking performance. In addition, a safety constraint on the maximum reactor temperature in the case of cooling failure is implemented. A PI controller is implemented for the first batch iteration to generate starting data and serve as a benchmark, providing observations for initial GP model training. The results show that, with observations from just two polymerization batches, tracking performance of GP-based NMPC quickly converges within 0.02°C for the noiseless case, on par with the full-model NMPC benchmark. The presence of measurement noise is also studied over 10 simulations to prevent bias. With noisy observations, a tracking performance of 0.12°C is achieved with convergence after 4 batches. This control performance is even better compared to 0.16°C from the full-model NMPC in this case study, suggesting the advantage of probabilistic GP for stochastic NMPC. We show a reduction of 97% and 82% in control error by the proposed iterative scheme in comparison with PI control, with and without measurement noise respectively. The GP-NMPC also outperforms linear MPC with the same iterative scheme in terms of constraint violation. In conclusion, the proposed iterative scheme enables the adoption of NMPC without existing models and abundant data for the control of batch processes. Future work includes the implementation of probabilistic constraints to improve robustness and safety of GP-NMPC.
References:
1. B. Srinivasan and D. Bonvin, “Stability and Controllability of Batch Processes,” IFAC Proc. Vol., vol. 39, no. 2, pp. 493–500, Jan. 2006, doi: 10.3182/20060402-4-BR-2902.00493.
2. D. Q. Mayne, J. B. Rawlings, C. V. Rao, and P. O. M. Scokaert, “Constrained model predictive control: Stability and optimality,” Automatica, vol. 36, no. 6, pp. 789–814, Jun. 2000, doi: 10.1016/S0005-1098(99)00214-9.
3. F. Fiedler, B. Karg, L. Lüken, D. Brandner, M. Heinlein, F. Brabender and S. Lucia “do-mpc: Towards FAIR nonlinear and robust model predictive control,” Control Eng. Pract., vol. 140, p. 105676, Nov. 2023, doi: 10.1016/J.CONENGPRAC.2023.105676.
4. L. Hewing, J. Kabzan, and M. N. Zeilinger, “Cautious Model Predictive Control using Gaussian Process Regression,” IEEE Trans. Control Syst. Technol., vol. 28, no. 6, pp. 2736–2743, May 2017, doi: 10.1109/TCST.2019.2949757.
5. E. Bradford, L. Imsland, D. Zhang, and E. A. del Rio Chanona, “Stochastic data-driven model predictive control using Gaussian processes,” Comput. Chem. Eng., vol. 139, p. 106844, Aug. 2020, doi: 10.1016/J.COMPCHEMENG.2020.106844.