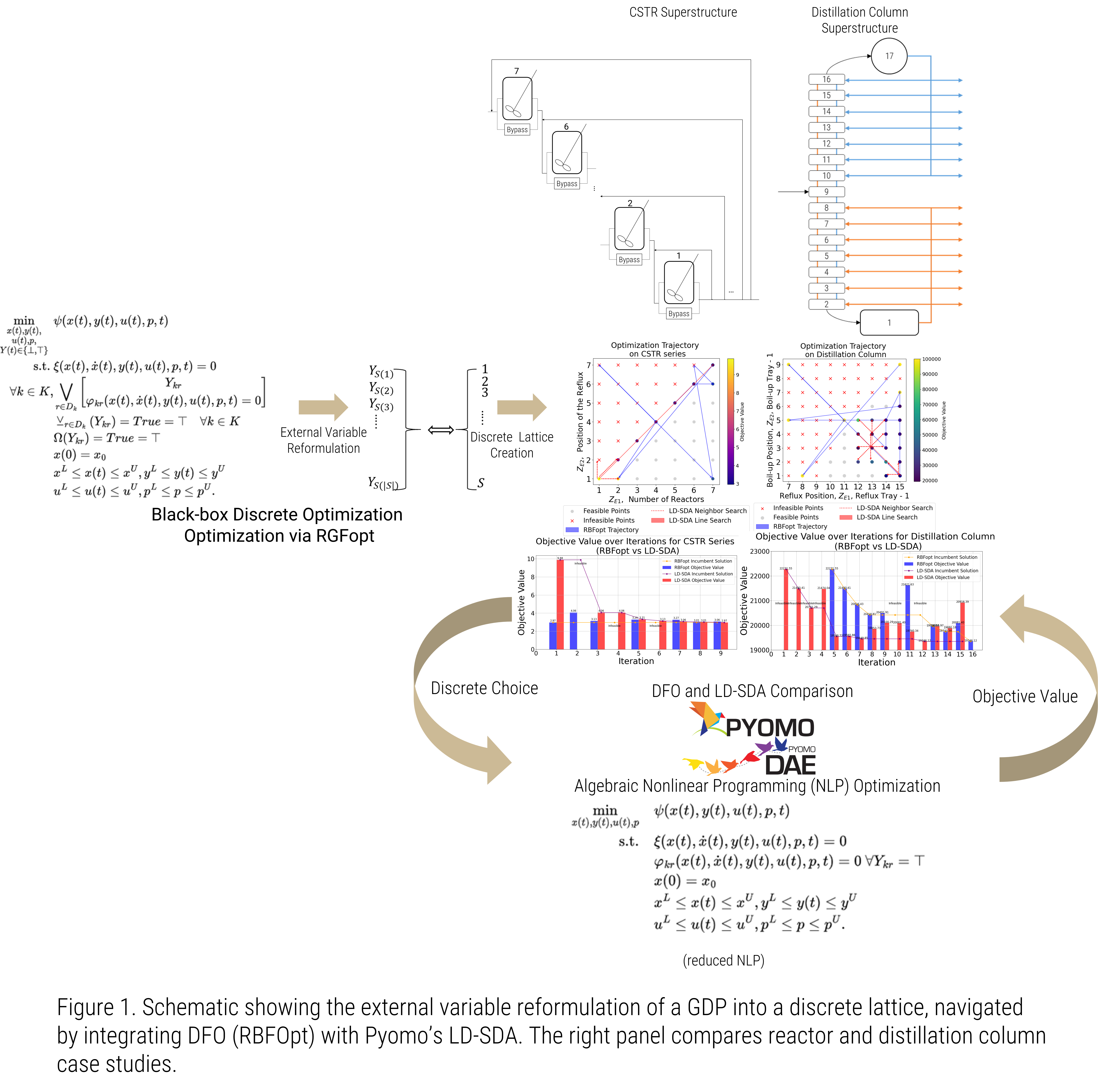
The Logic-Based Discrete-Steepest Descent Algorithm (LD-SDA) is an optimization method for solving GDP problems with ordered Boolean variables [1]. LD-SDA reformulates the problem by introducing external variables that represent the index of the active disjunct within each disjunction. These external variables define a discrete lattice, where each point corresponds to a fixed Boolean configuration and its associated reduced subproblem. The algorithm performs a steepest descent search over this lattice, systematically evaluating neighboring configurations and selecting the one that yields the greatest improvement in objective value. Therefore, LD-SDA efficiently navigates the combinatorial landscape of discrete decisions, enabling rapid identification of high-quality solutions within complex logical structures. Moreover, LD-SDA outperformed conventional approaches in solving not only the static GDP problem but also the dynamic GDP problem [2]. Notably, LD-SDA is available in the Pyomo GDP opt library [3] (https://github.com/Pyomo/pyomo).
However, despite the effectiveness of LD-SDA, its performance can degrade significantly for large-scale problems with many discrete choices. In these cases, LD-SDA may need to evaluate numerous subproblems corresponding to each fixed Boolean configuration, substantially increasing computational costs. Such exhaustive evaluation becomes increasingly impractical as the size and complexity of the discrete decision space grow, leading to inefficiency and limiting the scalability of LD-SDA. Derivative-Free Optimization (DFO) techniques offer a promising solution to alleviate these issues. Here, we propose integrating DFO methodologies, such as Radial Basis Function Optimization (RBFOpt) [4-6], to the integer lattice obtained from the external variable reformulation of the GDP. By intelligently utilizing the external variable reformulation of GDP, DFO techniques can efficiently navigate the discrete search space to identify promising candidate solutions rapidly. This integration can substantially reduce the number of subproblem evaluations required, thereby significantly improving the computational efficiency and scalability of the LD-SDA.
Preliminary results from the reactor series indicate that the integrated DFO approach applied to the external variable lattice converged in fewer iterations than LD-SDA. In contrast, tests on distillation column configurations indicated lower efficiency. These findings suggest that while the method can expedite the search in complex, high-dimensional settings, its advantages are less pronounced in low-dimensional cases. The proposed integration of DFO techniques holds significant promise for enhancing computational efficiency and scalability across various GDP applications for both static and dynamic problems.
References
[1] Ovalle, D., Liñán, D. A., Lee, A., Gómez, J. M., Ricardez-Sandoval, L., Grossmann, I. E., & Bernal Neira, D. E. (2025). Logic-Based Discrete-Steepe'st Descent: A Solution Method for Process Synthesis Generalized Disjunctive Programs. Computers & Chemical Engineering, 108993.
[2] Peng, Z., Lee, A., & Bernal (2024, October). Addressing Discrete Dynamic Optimization Via a Logic-Based Discrete-Steepest Descent Algorithm. In 2024 AIChE Annual Meeting. AIChE.
[3] Chen, Q., Johnson, E. S., Bernal, D. E., Valentin, R., Kale, S., Bates, J., ... & Grossmann, I. E. (2022). Pyomo. GDP: an ecosystem for logic based modeling and optimization development. Optimization and Engineering, 23(1), 607-642.
[4] Costa, A., & Nannicini, G. (2018). RBFOpt: an open-source library for black-box optimization with costly function evaluations. Mathematical Programming Computation, 10, 597-629.
[5] Nannicini, G. (2021). On the implementation of a global optimization method for mixed-variable problems. Open Journal of Mathematical Optimization, 2, 1-25.
[6] Ploskas, N., & Sahinidis, N. V. (2022). Review and comparison of algorithms and software for mixed-integer derivative-free optimization. Journal of Global Optimization, 82(3), 433-462.