Air separation units (ASUs), which produce high-purity oxygen, nitrogen, and argon from atmospheric air, are prime candidates for implementing DR strategies. These facilities consume significant amounts of electricity, amounting to 2.55% of U.S. manufacturing sector electricity [1], and their products can be stored cryogenically, allowing for temporal decoupling of production and demand. However, the complex dynamics and strict operational constraints of ASUs pose challenges for DR implementation.
This work presents a hierarchical framework for demand response optimization in air separation units that combines reinforcement learning (RL) with Linear Model Predictive Control (LMPC). We investigate two control architectures: a direct RL approach and a control-informed methodology where an RL agent provides setpoints to a lower-level LMPC. The proposed RL-LMPC framework demonstrates improved sample efficiency during training and better constraint satisfaction compared to direct RL control.
Optimization-based methods have been widely studied for ASU scheduling and control in DR contexts. Recent work has explored top-down approaches using scale-bridging models with linear MPC (LMPC) [2] and bottom-up strategies employing Economic Nonlinear MPC (eNMPC) [3]. While these methods have shown promise, they face limitations in practical implementation. They rely on accurate process models, which can be challenging to develop and maintain for ASUs [4]. Additionally, computational solution of large-scale optimization problems in real time can be prohibitive.
RL offers an alternative, data-driven approach that can potentially overcome some of these limitations. RL agents can learn to approximate optimal control policies directly from process data and interactions. Once trained, RL policies generally enable quick real-time inference, avoiding the computational burden of online optimization. However, the direct application of RL to complex chemical processes such as ASUs faces challenges in terms of sample efficiency, stability, and constraint satisfaction. RL is particularly well-suited for stochastic systems, as it inherently learns policies that can handle uncertainty and variability in process dynamics, enabling robust control even when faced noise in measurements.
In our work, we propose a practical method that combines the strengths of RL and MPC for ASU control in DR scenarios. Specifically, we investigate a hierarchical framework that integrates the scheduling decisions of an RL agent with a lower-level LMPC system. This approach aims to leverage RL’s learning capabilities and forward-inference efficiency while benefiting from MPC’s stabilizing effect on the learning process. We opt for linear MPC over non- linear MPC due to its faster inference time, ensuring it doesn’t detract from RL’s computational efficiency, though this comes at the cost of some control performance. For the RL component, we employ the Deep Deterministic Policy Gradient (DDPG) algorithm for policy optimization throughout this work, although the proposed method is agnostic to the choice of RL algorithm. DDPG combines elements of both policy-based and value-based methods, utilizing an actor-critic architecture that has proven effective for continuous control tasks [5].
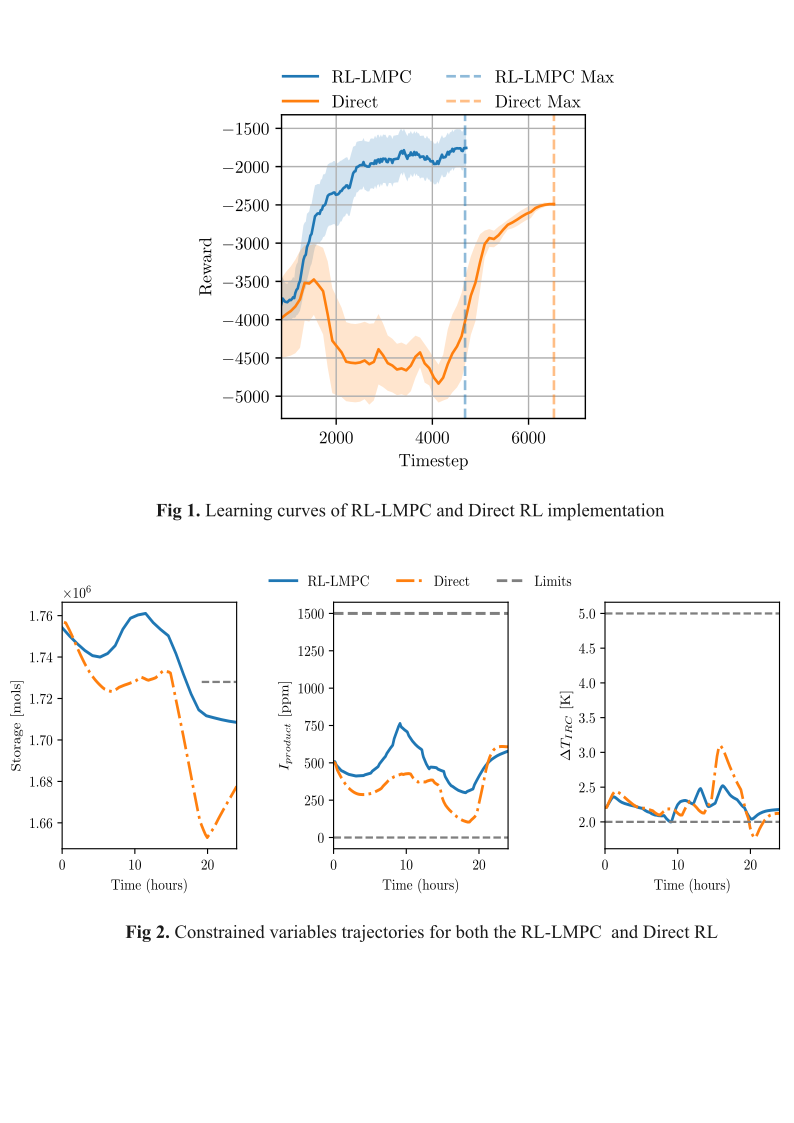
The ASU used as the case study is an openly available benchmark process for flexible operation problems [6]. The ASU’s main process unit is a single cryogenic distillation column that produces high-purity nitrogen product. Our experimental results demonstrate that both RL-control approaches successfully implement load-shifting strategies in response to electricity price variations. However, the RL-LMPC framework shows more efficient learning by converging to a high-quality policy after approximately 4000 timesteps, while the direct RL method required nearly 7000 timesteps to improve its final performance (Figure 1). This faster learning rate of the RL-LMPC can be attributed to the embedded LMPC reducing the exploration space by handling constraints explicitly, thereby allowing the RL agent to focus on optimizing the control policy within a feasible operating region.
In terms of constraint satisfaction, both agents successfully maintain product impurity within specified bounds throughout the operational period (Figure 2). However, a significant performance divergence occurs in the IRC temperature difference constraint, where the direct RL agent notably violates the lower bound. The RL-LMPC agent, benefiting from its embedded linear constraint model in the lower-level LMPC, successfully avoids such violations. This superior performance stems from the LMPC’s explicit constraint handling mechanism, which reduces constraint-violating actions from the RL agent’s exploration space, demonstrating a key advantage of the hybrid approach in managing operational constraints.
The proposed RL-LMPC framework offers a practical solution for implementing flexible operation strategies in process industries, bridging the gap be- tween data-driven methods and traditional control approaches. However, both agents struggle to satisfy terminal constraints which is the basis for future work. This future work will focus on incorporating model-based planning to allow the agent to assess future constraint satisfaction. The framework can also be extended to incorporate stochastic electricity price distributions and varying initial storage levels, helping advance the practical implementation of RL-based strategies in industrial process scheduling.
[1] Richard C. Pattison et al. “Optimal Process Operations in Fast-Changing
Electricity Markets: Framework for Scheduling with Low-Order Dynamic
Models and an Air Separation Application”. en. In: Ind. Eng. Chem. Res.
55.16 (Apr. 2016), pp. 4562–4584. (Visited on 10/08/2024).
[2] Lisia S. Dias et al. “A simulation-based optimization framework for inte-
grating scheduling and model predictive control, and its application to air
separation units”. en. In: Comput. Chem. Eng. 113 (May 2018), pp. 139–
151. issn: 00981354. (Visited on 10/02/2024).
[3] Adrian Caspari et al. “The integration of scheduling and control: Top-
down vs. bottom-up”. en. In: J. Process Control 91 (2020), pp. 50–62.
issn: 09591524. (Visited on 08/01/2024).