(390av) An Integrated Approach to Flowsheet Optimization of Pharmaceutical Manufacturing Process

Flowsheet optimization plays a crucial role in process design by enabling informed decision-making through quantitative technical and economic analyses. Due to the complexity of pharmaceutical processes, simulation-based optimization frameworks are often used, decomposing problems into process synthesis and operating conditions optimization. Typically, the configuration problem is solved first, followed by optimization of operating conditions at a fixed configuration. Due to demanding computational efforts of simulations, current existing approaches are often limited to only few configuration evaluations as a result, and this selection of flowsheets for evaluation lacks a systematic framework for decision-making and often relies on heuristic rules.

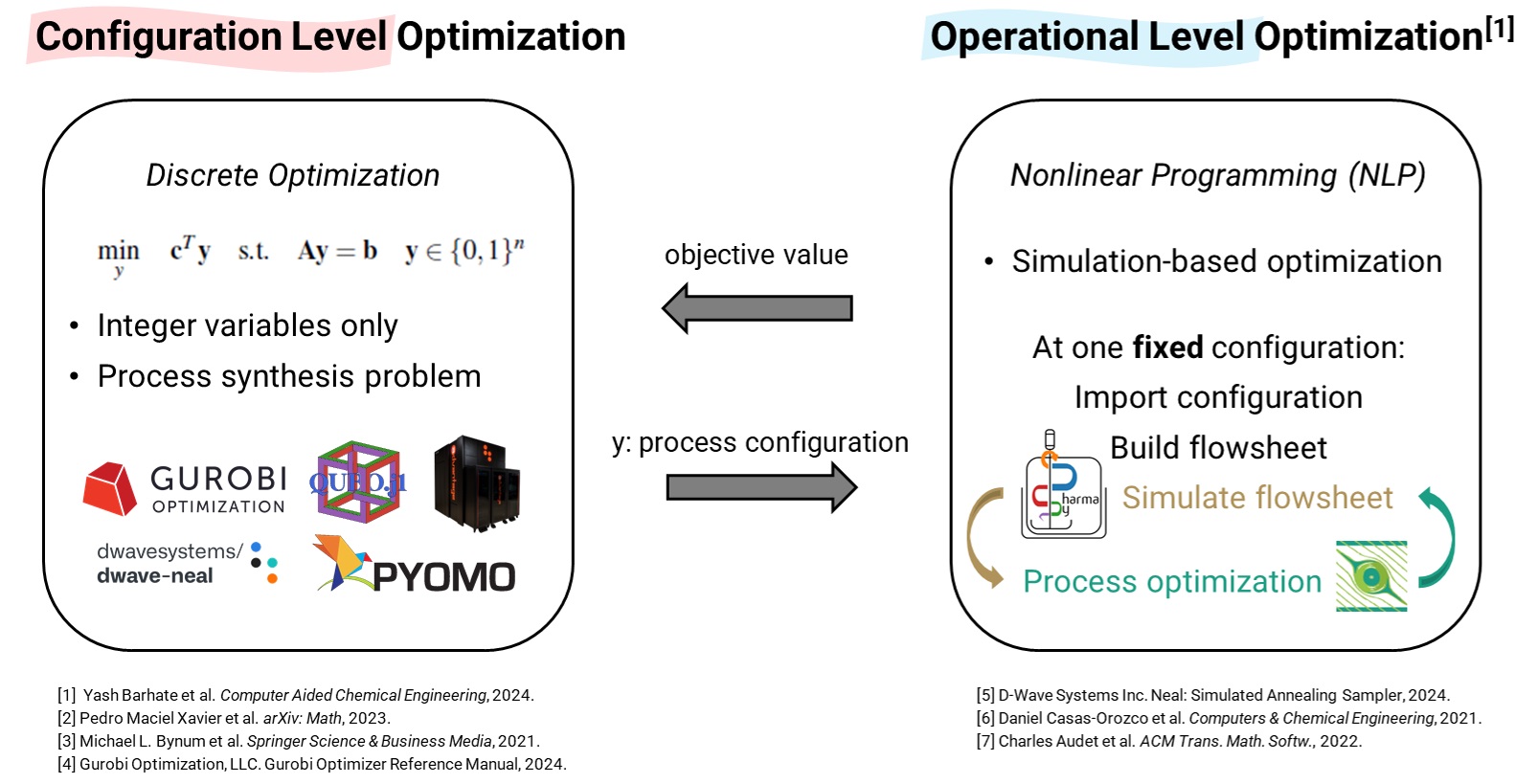
This work investigates the integration of mathematical programming through quantum and classical methods to enhance flowsheet optimization for an integrated process optimization approach. The design problem is formulated as a discrete optimization problem and solved using branch-and-bound (BnB), simulated annealing (SA), and quantum annealing (QA). A case study involving a drug substance synthesis process was conducted to minimize capital cost using binary decision variables for unit selection, mass balance, and logical constraints. BnB iteratively identified feasible solutions, while SA and QA addressed the problem as a quadratic unconstrained binary optimization (QUBO) problem. Preliminary results show BnB achieved the fastest optimality (<1 ms) and feasibility (79 ms), whereas QA took the longest (6.8 s). However, QA demonstrated advantages in solution diversity, identifying 28/36 feasible solutions in a single run compared to BnB’s iterative approach. QA offers potential for rapidly exploring large-scale process configurations where exhaustive classical searches are infeasible.

Combined with simulation-based operational optimization, this framework provides insights into how design-level decisions impact performance. It serves as a decision-making tool for selecting process designs based on economic and operational factors. Future work will refine QUBO formulations for QA and explore hybrid quantum-classical optimization methods.