(125b) Global and Robust Optimisation for Non-Convex Quadratic Programs

Robust optimisation aims to find solutions that remain feasible for all values within a given uncertainty set while optimising for the worst-case scenario. The main challenge lies in reformulating the uncertain problem into a deterministic, tractable form. For nonlinear convex problems, convex analysis can enable such reformulations for convex uncertainty sets. However, in many practical cases, a local robust solution is insufficient, requiring a combination of robust and global optimisation techniques. In [1], a tailored branch-and-bound algorithm was applied to scheduling crude oil operations under demand uncertainty, deriving the robust counterparts of the uncertain constraints. The robust pooling problems using both dual reformulations and cutting plane methods was evaluated in [2] while adaptively adjusting the tolerance of the global solver. In [3], a robust cutting set algorithm was developed to certify robust solutions for non-convex problems with many equalities. Additionally, [4] applied enhanced multiparametric disaggregation (ENMDT) and bound tightening to solve refinery planning under uncertainty. [5] proposed a global optimisation method that bypasses convexity by iteratively relaxing constraints in the outer minimisation problem, relying instead on continuity. The robustness and optimality of these solutions often depend on the solver used being either robust optimal or robust feasible.

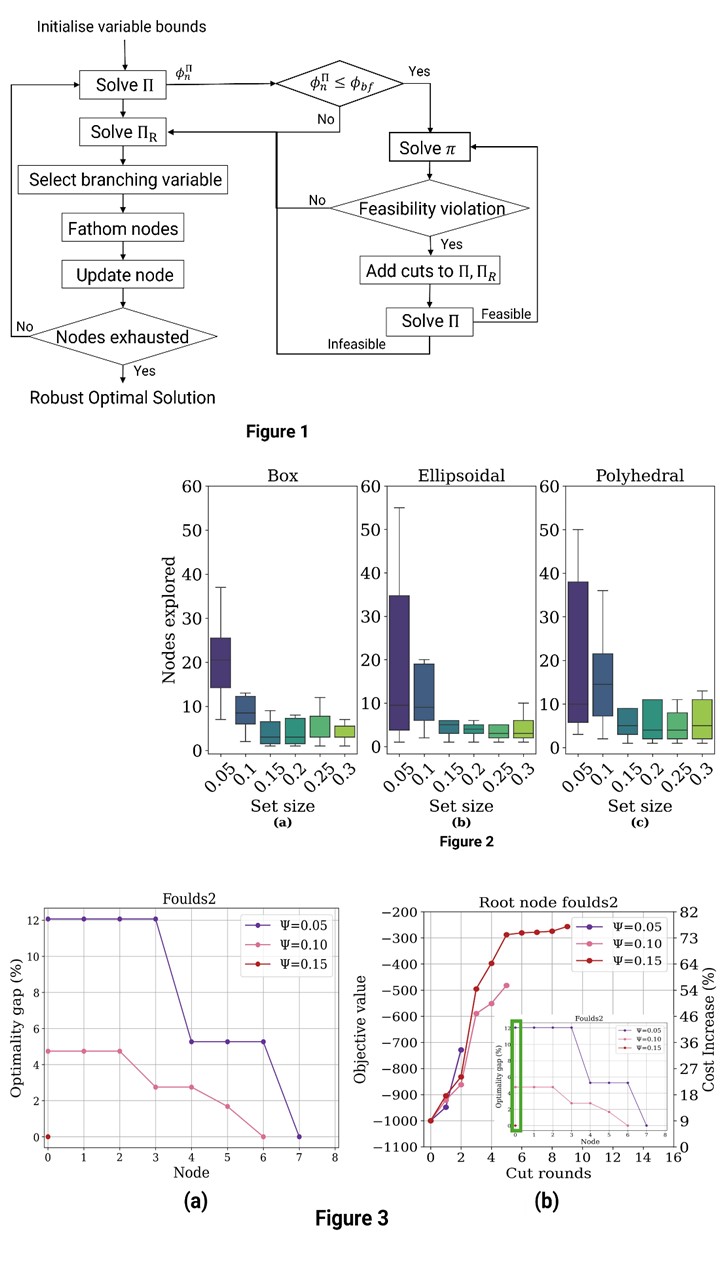
Our research hypothesis is that the integrated exploration of global and robust optimality can yield computational benefits. To this end, we have introduced a novel algorithm that conducts a concurrent global optimality and robustness search for continuous non-convex problems [6]. The key idea of the Robust spatial-Branch-and-Bound (RsBB) algorithm is that while exploring the branch-and-bound tree, we assess the robustness of nodes entailing the best-found solutions. In the proposed Robust-spatial-Branch-and-Bound algorithm (RsBB), we aim to integrate the robust cutting planes with the spatial Branch-and-Bound (sBB) algorithm. Relying on a local NLP solver, the proposed algorithm is evaluating the robustness of the solutions in a branching tree. The outline of the proposed algorithm is presented in Figure 1. The performance and benefits of our proposed approach is assessed via benchmark Quadratically Constrained Quadratic Programs (QCQPs) of pooling problems. For the original non-convex pooling problem we derive the convex relaxation using McCormick envelopes . For the initial variable bounds at the root node, problem is solved using a local solver. If the computed solution at a node is as good as the best-found so far , an infeasibility test is performed to evaluate the robustness of the obtained solution. The infeasibility test entails solving linear problems that aim to maximise the uncertain constraint violation. If such a violation occurs, then the corresponding robust cuts are added both to and . The cutting plane algorithm continues at the root node until no more robustness violations are detected. Until this step, the proposed algorithm follows the typical robust cutting plane algorithm. The following steps of the algorithm correspond the Branch-and-Bound algorithm. The branching variable is selected based on the maximum approximation error and a pseudoscore evaluation. The branching point is selected as the bisection in the domain of the selected branching variable. Nodes for which the solution is greater than the best-found solution of are fathomed. The next node is updated as the waiting node with the lowest solution. If the waiting nodes are exhausted, the robust optimal solution of the problem is obtained.

For the computational experiments we evaluate the performance of the RsBB algorithm for 10 benchmark pooling problems under feed quality uncertainty for box, ellipsoidal and polyhedral uncertainty sets of varying size. Figure 1 shows that the number of tree nodes explored by the RsBB algorithm generally decreases as the uncertainty set size increases. For set sizes above 0.15, all set types lead to fewer than 15 nodes, with little variation. At smaller sizes, variability increases, with the box set requiring the most nodes, followed by ellipsoidal and polyhedral. This is due to the box set representing the most conservative uncertainty, while ellipsoidal and polyhedral sets require more iterations to capture extreme parameter combinations. For the foulds2 problem (Figure 3) increasing the uncertainty size (Ψ) reduces RsBB iterations, and the root node optimality gap. Figure 3b shows that for Ψ = 0.15, 11 robust cut iterations lead to the robust optimal solution, while Ψ = 0.1 results in fewer cuts and a higher gap. Overall, greater conservatism—via set size or type—improves RsBB performance by tightening the feasible region through robust cuts.

In conclusion, the proposed RsBB algorithm combines the principles of spatial branch-and-bound (sBB) and robust cutting planes to solve continuous non-convex problems under convex uncertainty sets. The proposed approach is applied to QCQP pooling problems utilising McCormick envelopes to obtain convex lower bounds. The inlet quality parameter was treated as uncertain, with its range defined by box, ellipsoidal, and polyhedral uncertainty sets of varying sizes. We observed that using robust cutting planes in the sBB algorithm serves as an effective feasibility bounds tightening method. Finally, the integration of robust cuts is proven to have a beneficial impact on the sBB algorithm facilitating the optimality search both in terms of problem tractability and CPU time. Ongoing work in our work is looking into extending this approach to general non-convex problems.

Acknowledgements
Financial support under the EPSRC grant ADOPT (EP/W003317/1) is gratefully acknowledged by the authors.

References

[1] Li, J., Misener, R., & Floudas, C. A. (2011). Scheduling of Crude Oil Operations Under Demand Uncertainty: A Robust Optimization Framework Coupled with Global Optimization. AIChE Journal, 58, 2373–2396. https://doi.org/10.1002/aic.12772

[2] Wiebe, J., Cecĺlio, I., & Misener, R. (2019). Robust Optimization for the Pooling Problem. Industrial and Engineering Chemistry Research, 58(28), 12712–12722. https://pubs.acs.org/doi/full/10.1021/acs.iecr.9b01772

[3] Isenberg, N. M., Akula, P., Eslick, J. C., Bhattacharyya, D., Miller, D. C., & Gounaris, C. E. (2021). A generalized cutting-set approach for nonlinear robust optimization in process systems engineering. AIChE Journal, 67(5), e17175. https://doi.org/10.1002/AIC.17175

[4] Zhang, L., Yuan, Z., & Chen, B. (2021). Refinery-wide planning operations under uncertainty via robust optimization approach coupled with global optimization. Computers & Chemical Engineering, 146, 107205. https://doi.org/10.1016/J.COMPCHEMENG.2020.107205

[5] Mitsos, A., Tsoukalas, A. (2015). Global optimization of generalized semi-infinite programs via restriction of the right hand side. Journal of Global Optimization 61, 1–17. https://doi.org/10.1007/S10898-014-0146-6

[6] Marousi A., Charitopoulos V. M. (2025). Global and Robust Optimisation for Non-Convex Quadratic Programs. arXiv preprint. arXiv:2503.07310