There are some specific models that address process design across multi-scale variability, but their specialization makes it difficult to efficiently compare diverse processes to each other and is a bottleneck in advancing process implementation. There is yet no general optimization framework for this task. Towards this end, we develop a general optimization framework for the operation-informed design of chemical and energy systems subject to variability across multiple timescales. Our framework includes a general time structure, a canonical set of unit operation models and a process specific superstructure, as well as a corresponding mathematical program for numerical optimization. The time structure allows for variability to be captured at multiple timescales by representing the entire lifespan of a chosen system (horizon). The horizon is divided into sub-intervals called epochs, which capture system features over long timescales (ex: unit costs over the course of years). To capture features at intermediate timescales (ex: total solar irradiance in a day), epochs are further divided into segments. To capture still smaller timescales (ex: hourly change in electricity price), segments are divided into time steps and have an integer number of time points associated with them. An epoch is represented in the model by a period, which is a specific ordered combination of segments chosen from all segments in an epoch. This hierarchical structure allows for parameters and variables to be defined for time points, periods, epochs, and the horizon. The framework also includes a set of models for unit operations such as reactors, heat exchangers, separators, turbomachinery, and power generation/conversion equipment. These units are connected by streams that exchange mass and energy to represent a chemical/energy process as a superstructure. A corresponding model to the time structure and superstructure is formulated to enforce system constraints such as mass and energy balances on units, as well as relevant pressure-temperature relations. We also have constraints that enforce the capacity and operational flexibility of units across epochs, and these capacities are then used to determine capital costs. Subject to these constraints, an objective function that accounts for monetary and environmental cost over the entire horizon is minimized, effectively linking the various timescales together.
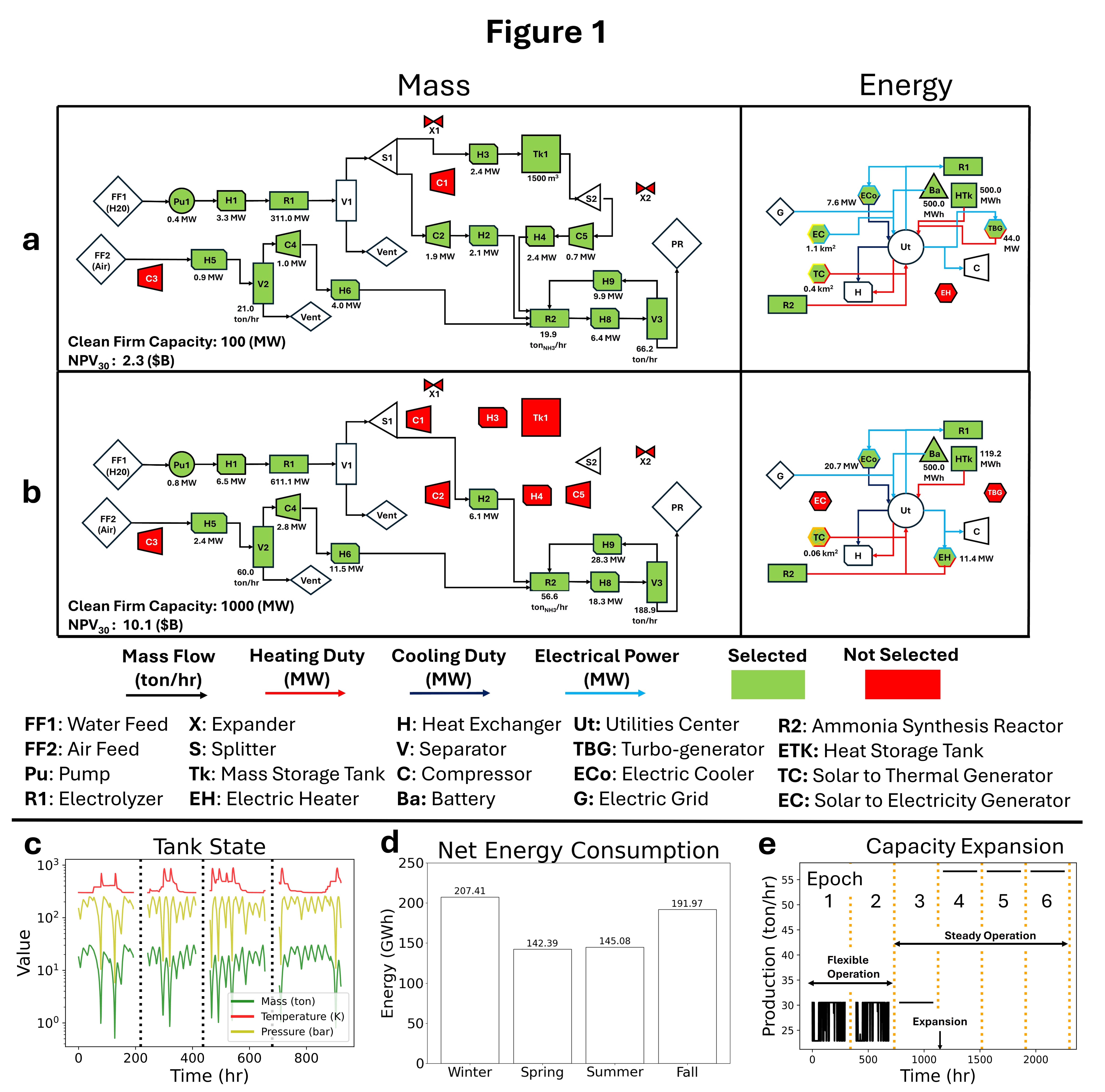
To demonstrate our framework, we present a case study on an electrolysis-based green ammonia synthesis process subject to hourly, seasonal, and multi-year variability in energy availability and pricing. The total time horizon is 30 years, and every epoch is five years. The epoch is represented by a period which corresponds to a representative year and is made from segments corresponding to single days containing 25 time points separated by one-hour. These segments are chosen from a set of days clustered by parametric similarity of solar irradiance, electricity price and grid emissions. They are ordered in the period to be representative of four periodic seasons. We first assume that all epochs are parametrically equivalent, and that process design and operation are repeated for every epoch. We consider a superstructure for an ammonia synthesis process that has limited flexibility. Nitrogen is supplied via cryogenic distillation of air, and hydrogen is produced from water electrolysis. The superstructure includes photovoltaic and concentrating solar units for onsite utilities generation; additionally, heat, electricity, and hydrogen can be stored via the use of tanks and batteries, if these units are selected.
We examine an optimal design and associated representative operation for this process when 100 (Figure 1a) or 1000 (Figure 1b) MW of clean power are available to the process from the grid. It is evident that with less clean firm power, the process is smaller and less profitable. It is designed with increased capacity for onsite utilities, as well as energy and mass storage, relative to the case when more clean power is available. We also observe operational behavior at different timescales, such as the hourly charge and discharge of mass storage (Figure 1c), seasonal changes in electricity purchase (Figure 1d), and occasional dips and spikes in the pressure, temperature, and holdup of mass storage tanks (Figure 1c). We then allow the design and operation to be distinct across epochs to examine how ammonia production capacity changes subject to rising ammonia demand (10 to 50 tons/hr), in a grid which expands its clean capacity for the process from 25 to 1000 MW over the course of the horizon. From this, we identify when the process shifts from flexible to steady operation and how the capacity changes in anticipation of rising demand (Figure 1e).
The developed optimization-based design framework allows us to better identify suitable candidates for the long-term transition towards sustainability. Our framework can be used to determine the optimal configuration, size, and representative operation of units, as well as relevant process state variables. This allows us to examine how the optimal design of a process changes in different cases and identify how optimal design evolves over the horizon. This demonstrates the utility of our framework in building useful insights about processes from the lenses of technical feasibility, financial attractiveness, and policy implication. We plan to further apply this framework to other sustainable processes.