(394ac) Gaussian Process Q-Learning for Finite-Horizon Markov Decision Processes

Many process control problems in chemical engineering require making decisions over a finite time horizon to maximize performance. This work presents a reinforcement learning framework that approximately solves finite-horizon Markov Decision Processes (MDPs) by combining Gaussian Processes (GPs) with Q-learning. Our proposed Gaussian Process Q-Learning (GPQL) algorithm demonstrates promising performance on problems with deterministic dynamics.

GPQL utilizes GPs to construct non-parametric approximations of state-action value functions at each decision stage through backward induction. This approach leverages the statistical modeling power of GPs and problem structure to provide both accurate function approximation and uncertainty quantification that can be exploited for exploration. The framework employs Thompson sampling [1] to balance exploration and exploitation during policy learning. To address the computational challenges associated with the cubic complexity of exact GP inference as datasets grow, we implement a principled subset selection mechanism using M-determinantal point processes (M-DPPs) [2, 3], which strategically selects representative state-action pairs that balance diversity and performance.

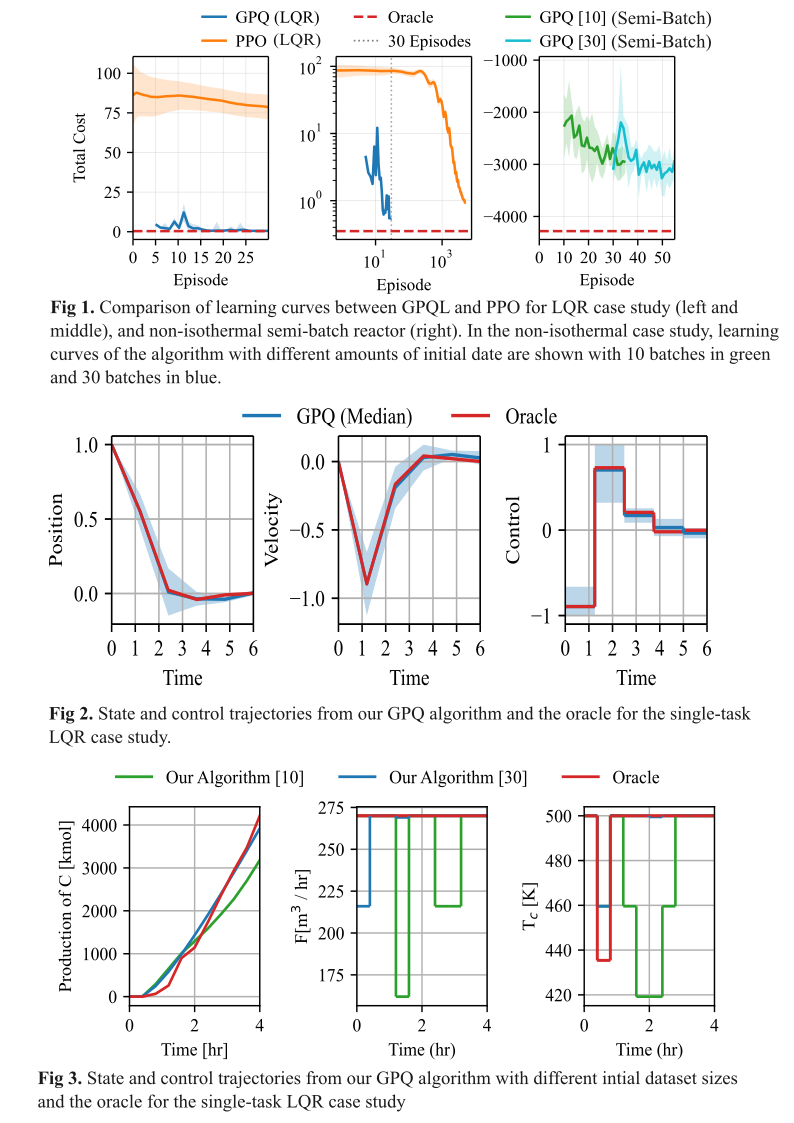
The effectiveness of GPQL is demonstrated first on a linear quadratic regulator (LQR) problem as a benchmark with a known analytical solution. As shown in Figure 1, our method achieves comparable performance to policy optimization approaches using neural networks with 100 times fewer data samples, demonstrating sample efficiency which is critical for systems where experimentation is costly. The learning curves presented in Figure 1 represent the Thompson sampling policy rather than the greedy policy, which explains the observed optimality gap that is not present when rolling out the greedy policy (Figure 2). For a more realistic application, we evaluate our approach on several chemical engineering examples, including a non-isothermal semi-batch reactor optimization problem with nonlinear dynamics [4]. In this case, the objective is to maximize the final amount of product C in a series reaction mechanism. Figure 3 demonstrates that with only 30 initial batches, GPQL approaches the performance of an oracle nonlinear model predictive controller with perfect system knowledge, confirming the method’s efficacy in practical chemical engineering applications. Our learned policy successfully tracks key state variables and control inputs generated by the oracle policy, with performance improving as the initial dataset size increases. Our results indicate that GPQL is particularly well-suited for chemical engineering applications where process models may be uncertain and experimentation is expensive.

In addition to empirical results, we present a theoretical analysis that establishes probabilistic uniform error bounds on the convergence of the GP posterior mean to the optimal state-action value
function for convex MDPs with deterministic dynamics. We derive asymptotic convergence rates and analyze how approximation errors propagate through the finite horizon, building on previous work by [5]. For convex MDPs with affine dynamics, we show that the state-action value function iterates remain in the same function class as the original cost function, enabling efficient and accurate
approximation.

This work contributes to process systems engineering by providing a sample-efficient, theoretically-grounded approach for solving single-task finite-horizon MDPs in continuous domains. The developed methodology bridges the gap between reinforcement learning theory and practical chemical engineering applications, offering a powerful tool for optimizing complex processes where traditional model-based approaches may be challenging to implement due to model uncertainty or complexity. In future work, we will extend GPQL to multi-task problems through a goal-conditioned setting, where the Q-function becomes a function of state, control input, and goal. This approach provides promise in handling changing setpoints due to varying process conditions, a common challenge in chemical processes, allowing for generalization across different production targets without requiring
retraining.

[1] James T. Wilson et al. Efficiently Sampling Functions from Gaussian Process Posteriors. en.
arXiv:2002.09309 [stat]. Aug. 2020. doi: 10.48550/arXiv.2002.09309. url: http://arxiv.
org/abs/2002.09309 (visited on 12/02/2024).
[2] Alex Kulesza, Ben Taskar, et al. “Determinantal point processes for machine learning”. In:
Foundations and Trends® in Machine Learning 5.2–3 (2012), pp. 123–286.
[3] Henry B. Moss, Sebastian W. Ober, and Victor Picheny. Inducing Point Allocation for Sparse
Gaussian Processes in High-Throughput Bayesian Optimisation. en. arXiv:2301.10123 [cs, stat].
Feb. 2023. url: http://arxiv.org/abs/2301.10123 (visited on 09/26/2024).
[4] Eric Bradford and Lars Imsland. “Economic Stochastic Model Predictive Control Using the Un-
scented Kalman Filter”. en. In: IFAC-PapersOnLine 51.18 (2018), pp. 417–422. issn: 24058963.
doi: 10.1016/j.ifacol.2018.09.336. url: https://linkinghub.elsevier.com/retrieve/
pii/S2405896318320196 (visited on 12/20/2024).