ANNs have significantly advanced the field of process monitoring by providing alternatives to traditional control charts and multivariate statistical techniques (e.g., PCA, PLS, ICA). Among ANNs, the MLP is widely used as the basis for more complex architectures. A multilayer perceptron comprises stacked layers in which each layer applies a nonlinear transformation to a biased linear combination of inputs. This configuration enables the network to learn and represent complex, hidden patterns in the data. However, MLP-based fault detection models often have limited interpretability and require extensive training data for satisfactory generalization.
Kolmogorov-Arnold Networks [6] (KANs) represent a recently proposed alternative that moves away from the traditional MLP design. Inspired by the Kolmogorov-Arnold representation theorem , KANs learn functional transformations along the edges of the network rather than applying fixed activation functions at the nodes. KANs were initially designed to perform quasi-symbolic regression tasks [5], mainly to recover analytical expressions from deterministic data in physics. The original implementation proposed to use B-splines to construct the edge functions, offering local adaptability but introducing computational complexity during training. In order to address this, subsequent research has proposed the use of other basis functions such as Radial Basis Functions [4] (FastKAN) , Fourier series [7] (FourierKAN), wavelets [1] (WavKAN), and orthogonal polynomials [3] (such as Legendre or Chebysev) to improve training stability, convergence speed, and model generalization.
Although KANs have strong theoretical foundations, their application in process monitoring and fault detection remains largely unexplored. In this study, we evaluate the performance of different KAN variants on the TEP benchmark to detect process faults. Rather than emphasizing interpretability, we focus on how well these models perform when data is scarce, which is often the case in real industrial settings. Because relatively small KANs can learn flexible mathematical relationships along the connections between neurons, we believe they can still detect faults accurately even when only a small amount of training data is available.
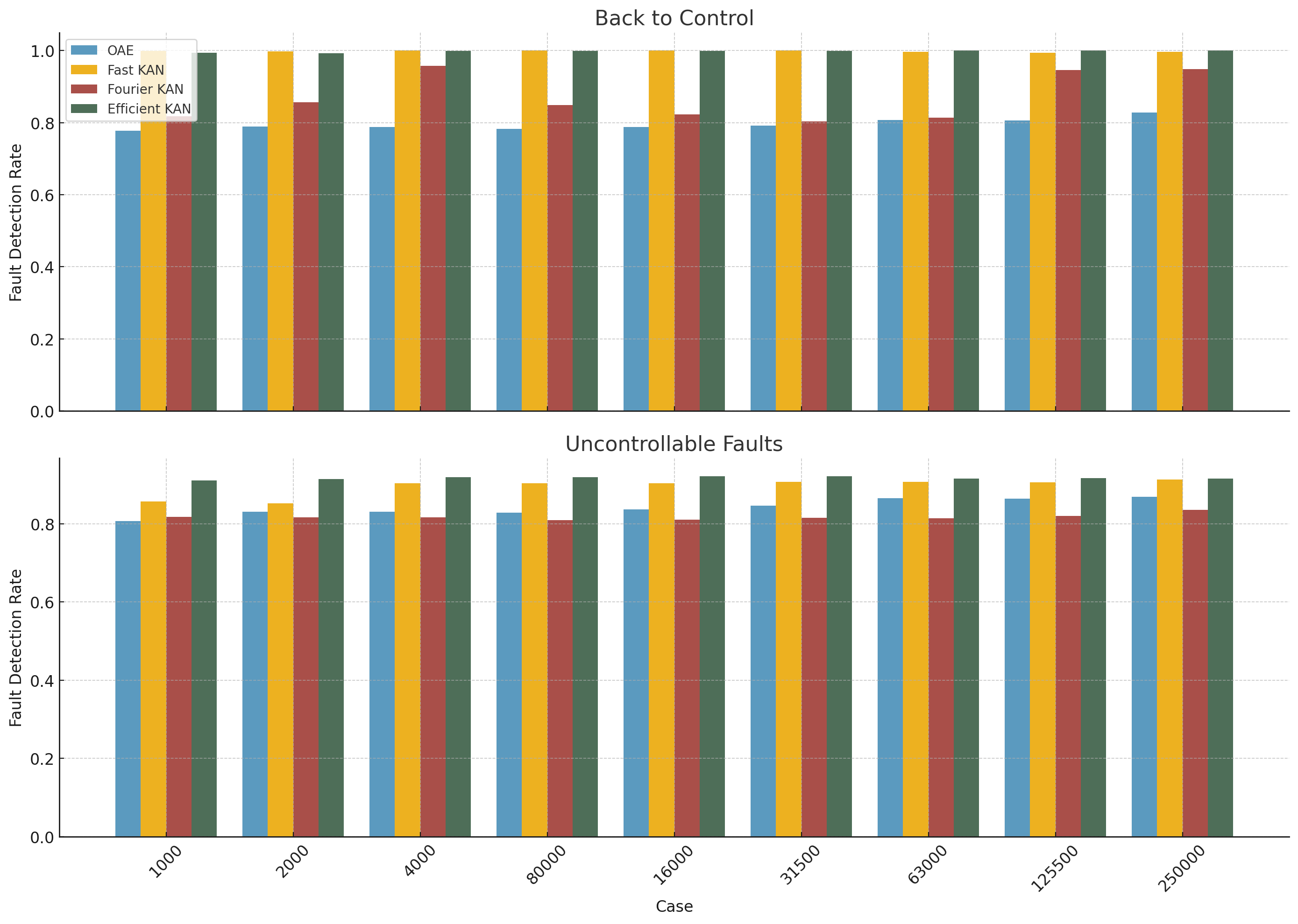
We evaluated three KAN variants, FastKAN [4], FourierKAN [7], and EfficientKAN (an optimized version of the original implementation of Liu et al. [6]), and compared their performance to the OAE presented in Cacciarelli et al. [2]. Each model was trained on datasets of different sizes, ranging from 500 to 250,000 observations. The models were tested on labeled TEP fault data and evaluated across three fault categories: (i) controllable faults, where process control can restore normal operating conditions; (ii) back-to-control faults, where the system transitions back to normal operation after a disturbance; and (iii) uncontrollable faults, which persist despite control action.
The results indicate that EfficientKAN and FastKAN consistently outperformed the Orthogonal Autoencoder across most dataset sizes. EfficientKAN stood out with the highest detection accuracy for uncontrollable faults and maintained low false positive rates even when trained on just 1,000 samples. Regarding back-to-control faults, both EfficientKAN and FastKAN achieved strong detection performance. FourierKAN showed similar results on larger datasets, but its accuracy dropped noticeably with limited training data. The Orthogonal Autoencoder, while stable, delivered more modest results and had particular difficulty detecting back-to-control faults.
These findings highlight the potential of KANs as powerful and data-efficient models for fault detection in complex industrial systems. Their flexible architecture enables accurate modeling of nonlinear processes even in situations with limited data. Our study provides evidence that KAN models can serve as a scalable and robust alternative to traditional MLP-based autoencoders for process monitoring.
Future directions include analyzing and comparing the learned functions to identify interpretable patterns and relationships. If interpretability is not readily apparent, regularization techniques could be explored to enhance the clarity of learned representations, particularly in high-dimensional datasets. Additionally, developing dynamic extensions that incorporate memory mechanisms or differential operators could enable KANs to better handle sequential data. These advancements have the potential to further broaden the applicability of KANs in industrial monitoring, control, and anomaly detection tasks.
References
[1] Zavareh Bozorgasl and Hao Chen. Wav-KAN: Wavelet Kolmogorov-Arnold Networks. 2024. arXiv: 2405.12832 [cs.LG].
[2] Davide Cacciarelli and Murat Kulahci. “A novel fault detection and diagnosis approach based on orthogonal autoencoders”. In: Computers Chemical Engineering 163 (2022), p. 107853. issn: 0098-1354.
[3] Tianrui Ji, Yuntian Hou, and Di Zhang. A Comprehensive Survey on Kolmogorov Arnold Networks (KAN). 2025. arXiv: 2407.11075 [cs.LG].
[4] Ziyao Li. Kolmogorov-Arnold Networks are Radial Basis Function Networks. 2024. arXiv: 2405.06721 [cs.LG].
[5] Ziming Liu et al. KAN 2.0: Kolmogorov-Arnold Networks Meet Science. arXiv: 2408.10205 [cs.LG].
[6] Ziming Liu et al. KAN: Kolmogorov-Arnold Networks. 2025. arXiv: 2404. 19756 [cs.LG].
[7] Jinfeng Xu et al. FourierKAN-GCF: Fourier Kolmogorov-Arnold Network an Effective and Efficient Feature Transformation for Graph Collaborative Filtering. 2024. arXiv: 2406.01034 [cs.IR]