2025 AIChE Annual Meeting

(392bg) Exact Hull Reformulation for Quadratically Constrained Generalized Disjunctive Programs

Authors

Generalized Disjunctive Programming (GDP) is a powerful modeling framework that represents Mixed-Integer Nonlinear Programs (MINLPs) using Boolean variables and disjunctions and is widely applied in Process Systems Engineering (PSE) and other optimization domains [1]. One of the most effective methods for solving GDP problems is the hull reformulation, which constructs a tighter relaxation than alternative methods such as the Big-M formulation [2]. However, hull reformulation introduces disaggregated variables and additional constraints, often increasing problem complexity. Moreover, the use of the perspective function, which is applied to constraints in disjunctions to create hull reformulation, presents a challenge since it is not a closed function, and the closure of the perspective function is required for hull reformulation. However, no closed-form expression exists for the closure of the perspective function in the general nonlinear case [3]. The most reliable workaround for this problem in general nonlinear functions involves ε-approximations proposed by Furman, Sawaya, and Grossmann [4], which is expressed as (cl h~)(x,y))≈((1-ε)y+ε)h(x\((1-ε)y+ε)) - εh(0)(1-y). Although this approximation is exact at the binary values of 0 and 1, it can become numerically unstable near zero for small values of ε. Also, its relaxation introduces an additional computational burden. For example, in the case of quadratic functions, the ε-approximation significantly complicates the formulation, requiring the use of general-purpose mixed-integer nonlinear programming (MINLP) solvers, and does not allow the use of specialized mixed-integer quadratic programming (MIQCP) solvers that are more efficient for quadratic structures. The ε-approximation not only complicates the formulation but also weakens the continuous relaxation compared to an exact hull reformulation. Consequently, the use of ε-approximation may obscure the problem structure and diminish solver performance, highlighting the need for exact methods when possible.

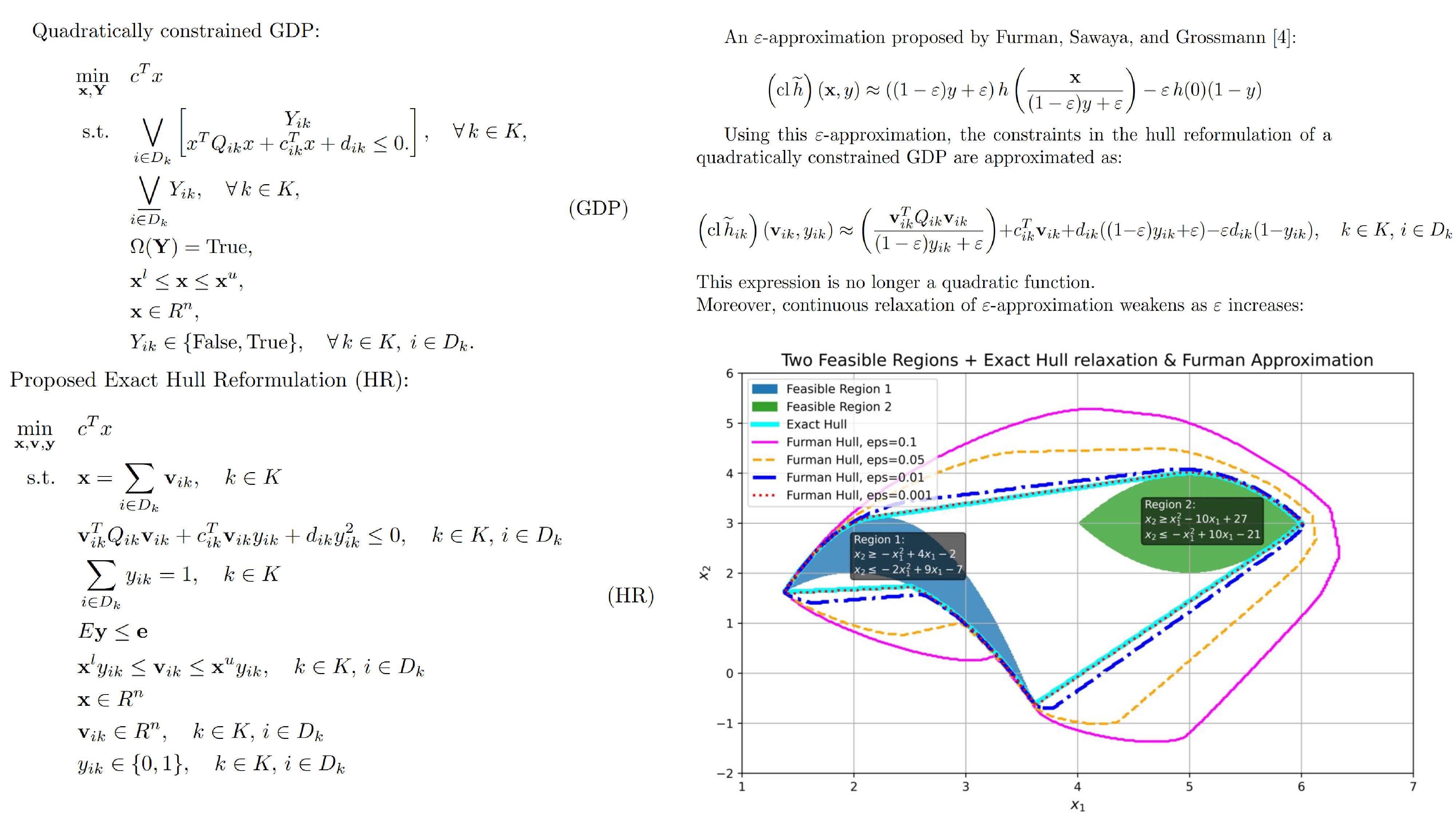
In this work, we show that a Quadratically Constrained GDP can be reformulated into an exact hull representation that preserves the quadratic structure of the original problem. Specifically, constraints of the form xTQx+cTx+d≤0 within a disjunction in hull reformulation approach can be replaced by vTQv+cTvy+dy2≤0, where v is a disaggregated variable and y is the binary variable associated with the disjunct. Therefore, we propose constructing exact hull reformulations of GDP with quadratic constraints, including non-convex quadratic constraints, avoiding the need for ε-approximation. We implement this approach in Pyomo [5] and benchmark it across several GDP-based problems previously reported in the literature, such as a Continuous Stirred-Tank Reactor (CSTR) network design [6], a constrained layout optimization, k-means clustering, and a set of randomly generated test instances [3]. All models are solved using Gurobi [7], a leading solver for Mixed-Integer Quadratically Constrained Programs (MIQCP)[8]. Our computational results demonstrate that the exact reformulation enables a more efficient solution to quadratic GDP problems compared to the ε-approximation approach. For instance, in the largest tested case involving a CSTR network [6] with 20 reactors, the exact hull reformulation achieved a 1.8x reduction in solution time relative to the ε-approximation method proposed by Furman, Sawaya, and Grossmann [4], which is the default option for handling any nonlinear constraints in Pyomo when applying hull reformulation. This performance gain highlights the practical advantage of preserving the quadratic structure and avoiding approximation-based complexity.

This study underscores the value of customized reformulations in GDP-based optimization. The proposed exact hull reformulation enables faster and more scalable solutions to quadratic GDP problems, offering practical advantages in real-world applications across Process Systems Engineering and other domains. While prior work has discussed the benefits of exact analytic hull reformulations for specific functions such as convex quadratics [9], most of the existing literature has focused primarily on convex disjunctive sets. In contrast, this work extends the scope by demonstrating the feasibility and impact of exact hull reformulations for disjunctive sets that are not necessarily convex. By enabling broader applicability and enhancing solver performance without approximation overhead, this contribution provides a novel and practically significant advancement in the use of GDP for modeling and solving complex optimization problems.

[1] I. E. Grossmann and F. Trespalacios, “Systematic modeling of discrete-continuous optimization models through generalized disjunctive programming,” AIChE J., vol. 59, no. 9, pp. 3276–3295, 2013, doi: 10.1002/aic.14088.

[2] I. E. Grossmann and S. Lee, “Generalized Convex Disjunctive Programming: Nonlinear Convex Hull Relaxation,” Comput. Optim. Appl., vol. 26, no. 1, pp. 83–100, Oct. 2003, doi: 10.1023/A:1025154322278.

[3] D. E. Bernal Neira and I. E. Grossmann, “Convex Mixed-Integer Nonlinear Programs Derived from Generalized Disjunctive Programming using Cones,” Feb. 19, 2024, arXiv: arXiv:2109.09657. doi: 10.48550/arXiv.2109.09657.

[4] K. C. Furman, N. W. Sawaya, and I. E. Grossmann, “A computationally useful algebraic representation of nonlinear disjunctive convex sets using the perspective function,” Comput. Optim. Appl., vol. 76, no. 2, pp. 589–614, Jun. 2020, doi: 10.1007/s10589-020-00176-0.

[5] M. L. Bynum et al., Pyomo — Optimization Modeling in Python, vol. 67. in Springer Optimization and Its Applications, vol. 67. Cham: Springer International Publishing, 2021. doi: 10.1007/978-3-030-68928-5.

[6] D. A. Liñán, D. E. Bernal, L. A. Ricardez-Sandoval, and J. M. Gómez, “Optimal design of superstructures for placing units and streams with multiple and ordered available locations. Part I: A new mathematical framework,” Comput. Chem. Eng., vol. 137, p. 106794, Jun. 2020, doi: 10.1016/j.compchemeng.2020.106794.

[7] “Gurobi Optimization, LLC.,” Gurobi Optimization. Accessed: Mar. 27, 2025. [Online]. Available: https://www.gurobi.com/

[8] T. Karia, C. S. Adjiman, and B. Chachuat, “Assessment of a two-step approach for global optimization of mixed-integer polynomial programs using quadratic reformulation,” Comput. Chem. Eng., vol. 165, p. 107909, Sep. 2022, doi: 10.1016/j.compchemeng.2022.107909.

[9] O. Günlük and J. Linderoth, “Perspective Reformulation and Applications,” in Mixed Integer Nonlinear Programming, vol. 154, J. Lee and S. Leyffer, Eds., in The IMA Volumes in Mathematics and its Applications, vol. 154. , New York, NY: Springer New York, 2012, pp. 61–89. doi: 10.1007/978-1-4614-1927-3_3.