(394a) Equivalent-Circuit Thermal Aging Model for Lithium-Ion Battery Temperature Prediction with Parameter Identification

Owing to attractive properties such as high energy density, long lifecycle, and low self-discharge rate, lithium-ion batteries have been widely employed for energy storage systems in numerous applications such as electric vehicles and portable devices [1]. Understanding and monitoring their thermal behaviors are essential for the safe and normal operation of battery-driven systems. Improper battery thermal management (e.g., exceeding the maximum permissible limit of 60^oC) can lead to accelerated degradation, reduced longevity, or even disastrous thermal runaway [2]. Traditional battery temperature estimation includes sensor-based, model-based, and data-driven methods. The sensor-based approaches employ temperature sensors that often require continuous calibration or are overly complex for online deployment [3-4]. Model-based approaches offer detailed insights, but the high-fidelity models are expensive to solve [5]. Data-driven approaches, particularly deep learning methods, have become prevalent; however, their performance heavily depends on the quality and quantity of the data, which are often limited in battery applications [6].

To address the above challenges, equivalent-circuit (EC) models have been studied for modeling battery thermal behaviors [7-8]. However, existing reported works on EC models still suffer from the following issues: (i) these models require extensive knowledge about material and thermal properties of the battery; (ii) the majority of these methods struggle to quantify the heat generation during battery charge-discharge cycles; and (iii) most studies overlook the effects of aging and battery degradation during the development of EC models. In this work, we aim to develop a novel, high-fidelity, adaptive, and computationally efficient EC thermal (ECT) model for battery temperature prediction to address the above issues. The proposed ECT model is analogous to the equivalent-circuit voltage model and thus easily deployable [9]. Specifically, we approximate the complex heat generation mechanism inside the battery with nonlinear functions of state-of-charge (SoC), current, and terminal voltage. Further, an aging factor, defined as a function of the state-of-health (SoH) and cycle number, is incorporated into the ECT framework (known as ECT-aging model) to capture the effects of battery degradation on temperature prediction. The parameter identification of the ECT-aging model is formulated into a least-squares problem that can be easily solved with available charging or discharging profiles.

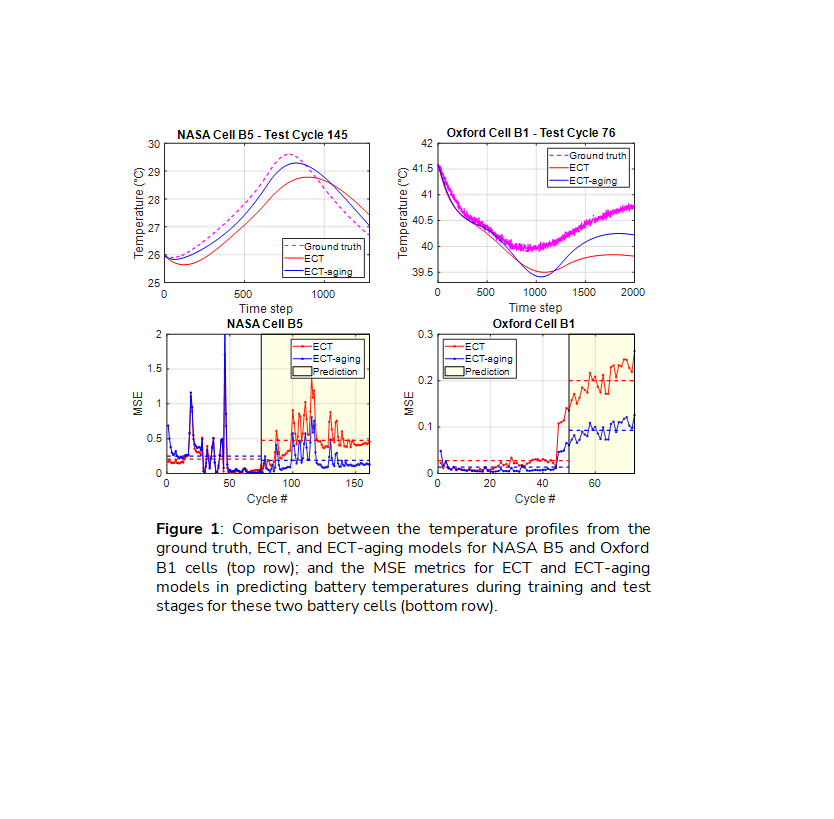
The presented ECT and ECT-aging models are thoroughly tested via benchmark NASA and Oxford datasets. For each case study, the data from early cycles are used for identifying the parameters. The established models are used for predicting the temperature of future (test) cycles. The mean-squared error (MSE) metric is used to assess the accuracy of the temperature prediction. In Fig. 1, the top row compares the temperature profiles from the ground truth, ECT model, and ECT-aging model for specific cycles #145 and #76 of NASA Cell B5 and Oxford Cell B1, respectively. The bottom row shows the MSE metrics of the ECT model and ECT-aging model during the training (white area) and test (yellow area) stages for these two cells. It is observed that at the test stage, the ECT-aging model can clearly outperform the ECT model by accounting for degradation factors, with an averaged improvement of 0.256^oC and 0.147^oC in the prediction accuracy, respectively for the two cells. These results demonstrate the effectiveness of the proposed ECT-aging model in depicting battery thermal behaviors by accounting for the capacity fade.

Reference

[1] Chao Lyu, Yankong Song, Dazhi Yang, Wenting Wang, Yaming Ge, and Lixin Wang. Online prediction for heat generation rate and temperature of lithium-ion battery using multi-step-ahead extended Kalman filtering. Applied Thermal Engineering, 231:120890, 2023.
[2] Davoud Mahboubi, Iraj Jafari Gavzan, Mohammad Hassan Saidi, and Naghi Ahmadi. Developing an electro-thermal model to determine heat generation and thermal properties in a lithium-ion battery. Journal of Thermal Analysis and Calorimetry, 147(21):12253–12267, 2022.
[3] Mahroo Sajid, Ala A Hussein, Ali Wadi, and Mamoun F Abdel-Hafez. An enhanced fusion algorithm with empirical thermoelectric models for sensorless temperature estimation of li-ion battery cells. IEEE/ASME Transactions on Mechatronics, 28(2):621–631, 2023.
[4] HPGJ Beelen, LHJ Raijmakers, MCF Donkers, PHL Notten, and HJ Bergveld. An improved impedance-based temperature estimation method for li-ion batteries. IFAC-PapersOnLine, 48(15):383–388, 2015.
[5] Xinfan Lin, Hector E Perez, Shankar Mohan, Jason B Siegel, Anna G Stefanopoulou, Yi Ding, and Matthew P Castanier. A lumped-parameter electro-thermal model for cylindrical batteries. Journal of Power Sources, 257:1–11, 2014.
[6] Pradeep Kumar, Gary Rankin, Krishna R Pattipati, and Balakumar Balasingam. Model-based approach to long term prediction of battery surface temperature. IEEE Journal of Emerging and Selected Topics in Industrial Electronics, 4(1):389–399, 2022.
[7] Wei Liu, Jiashen Teh, Bader Alharbi, Geng Yang, Bingzhang Wang, Deyue Meng, Jian Shi, Abdulrahman AlKassem, Ahmad Aljabr, and Naif Alshammari. An electric-thermal coupling modeling method for lithium-ion battery using the state of charge normalization calculation method. Journal of Energy Storage, 72:108724, 2023.
[8] Yusheng Zheng, Yunhong Che, Xiaosong Hu, Xin Sui, and Remus Teodorescu. Online sensorless temperature estimation of lithium-ion batteries through electro-thermal coupling. IEEE/ASME Transactions on Mechatronics, 2024.
[9] Ning Tian, Yebin Wang, Jian Chen, and Huazhen Fang. On parameter identification of an equivalent circuit model for lithium-ion batteries. In 2017 IEEE Conference on Control Technology and Applications (CCTA), pages 187–192. IEEE, 2017.