(601i) Effect of Pulsatile Flow on Dynamics of Surfactant-Laden Compound Droplet in Vertical Channel

Surfactants are often used to stabilize the core and shell of a compound droplet, which are employed across diverse sectors such as in diagnostics and therapeutics, microextraction and material science (cite). The interaction between unsteady external flows and surfactant-laden compound droplets plays a significant role in microfluidic and physiological environments where pulsatile flows are common (cite). Pulsatile flows periodically reverse flow direction, increasing the effective travel distance without the need for higher pressure thereby enhancing mixing. Pulsatile flow’s ability to mimic blood circulation makes it highly suitable for applications like organ-on-a-chip and drug delivery. This study, for the first time, presents a numerical investigation into the behaviour of a compound droplet in a vertical channel subjected to a time-periodic (pulsatile) flow, focusing on how the presence and distribution of surfactant on the core interface, shell interface, and simultaneously on both interfaces affects droplet dynamics.

Using a two-dimensional fast local level-set based inhouse solver, we capture the time-dependent evolution of the compound droplet interfaces and the redistribution of insoluble surfactant under varying hydrodynamic conditions. The simulations consider the effects of interfacial elasticity, surfactant coverage, Peclet number, and pulsation frequency on the deformation and migration of compound droplet. The imposed pulsatile flow induces oscillatory shear and pressure gradients, which in turn interact with interfacial Marangoni stresses arising from non-uniform surfactant concentration.

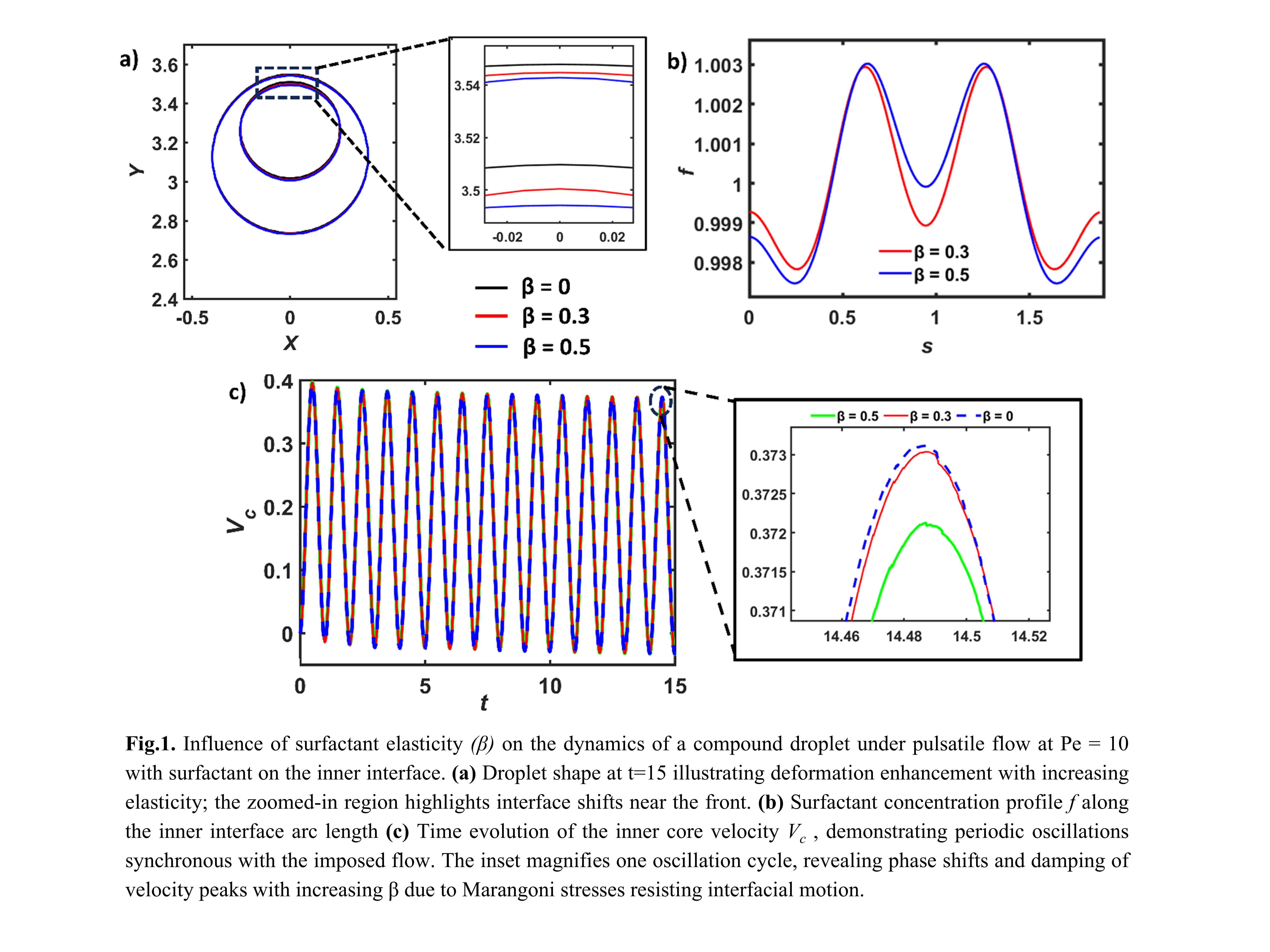
Our results reveal that the time-periodic nature of the external flow leads to cyclic deformation of the compound droplet and dynamic migration patterns that strongly depend on the phase lag between flow oscillation and surfactant relaxation. When surfactant is distributed on core interface as shown in Fig. 1 under pulsatile flow, the time-varying shear causes multiple peaks and valleys in the surfactant concentration (f) along the core interface. These arise from the oscillatory nature of the external flow, which continuously reorients the direction of surfactant transport. The resulting distribution reflects the interplay between flow pulsation, surface elasticity, and interfacial diffusion, giving rise to wave-like profiles. Higher elasticity number (β) dampens the droplet’s deformation and core velocity by strengthening Marangoni stresses that resist interfacial motion.

These findings contribute to our fundamental understanding of pulsatile flow dynamics and interfacial surfactant physics, while also guiding the optimal synthesis of surfactant-laden compound droplets.

References:

1. Stone, H. A., & Leal, L. G. (1990). The effects of surfactants on drop deformation and breakup. Journal of Fluid Mechanics, 220, 161–186.
2. Martinez, M. J., & Udell, K. S. (1990). Axisymmetric creeping motion of drops through circular tubes. Journal of Fluid Mechanics, 210, 565–591.
3. Zhu, L., & Brandt, L. (2015). Surfactant-laden drop in linear flows. Journal of Fluid Mechanics, 770, 374–397.