(523e) Disentangling Magnitudinal and Directional Contributions in Transient Degrees of Rate Control Calculations for Partial Oxidation Reactions with Cyclic Steady States

Formalisms for assessing the rate determining nature of elementary steps, including sensitivities and degrees of rate control, have been developed and applied widely under steady state conditions,^1,2 but not under under transient conditions. Specifically in the case of degrees of rate control, conservation criteria are violated when using degrees of rate control definitions developed at steady state, and additional terms that account for the sensitivity of the rate to the inverse of time have been proposed as a means for circumventing this issue.³ In this context, it is important to note that neither a universal definition of a transient degree of rate control nor a generalizable method for its calculation has been presented in the open literature thus far.

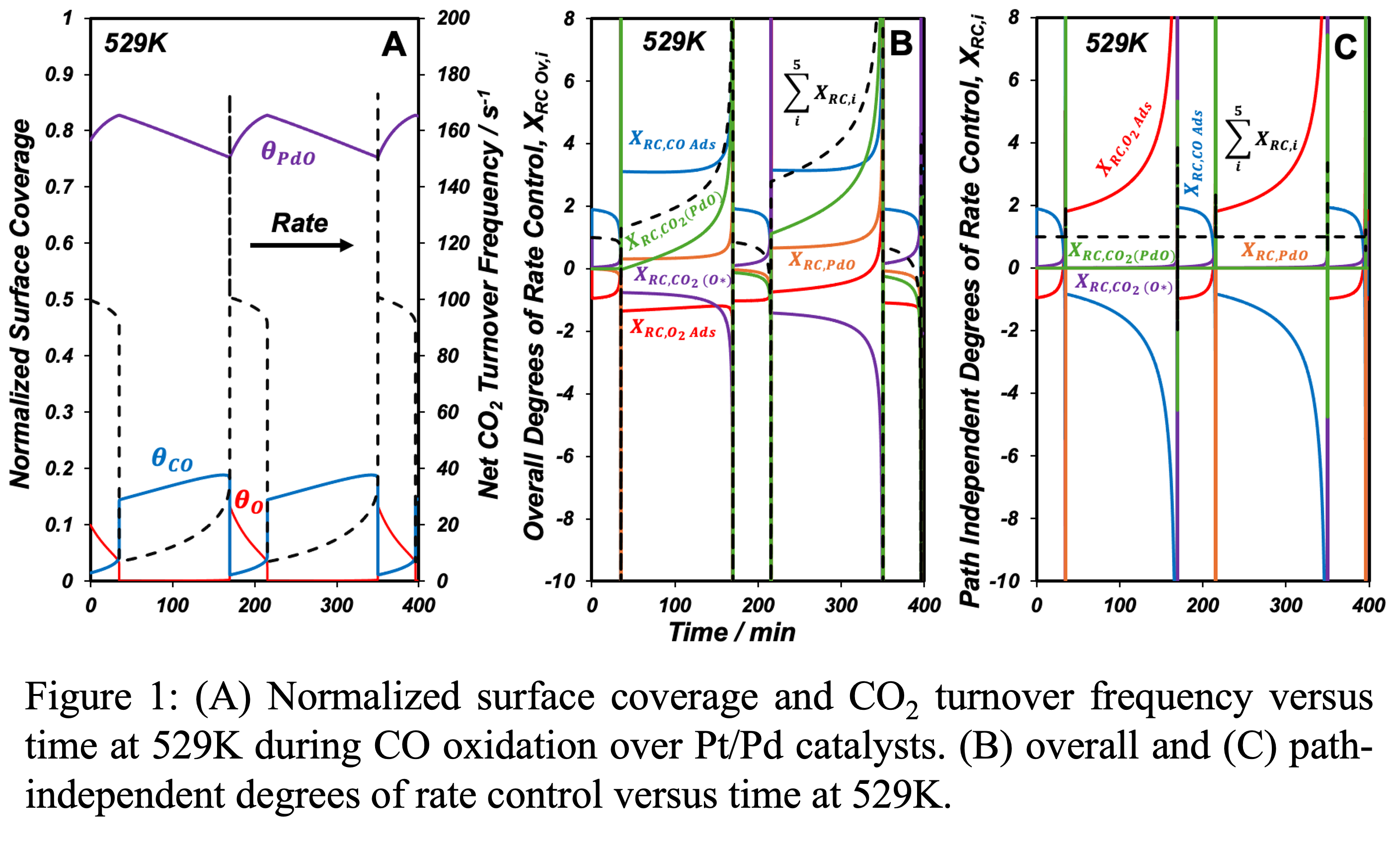
In this work, we use the special case of stable limit cycles to deconvolute path-dependent and path-independent degrees of rate control that carry the directional and magnitudinal contributions to the transient degrees of rate control (DRC). Applying the conventional DRC definition to a CO oxidation reaction system exhibiting oscillatory steady states (Figure 1A) yields uninterpretable results, as demonstrated by the calculations in Figure 1B. Figure 1C, on the other hand, plots path-independent DRCs which form regular patterns and sum to unity. Our work presents a novel, potentially generalizable formalism for assessing rate determining steps under transient conditions, and suggests paring of path-dependence (or directionality) as key to rigorously determining rate determining steps under transient conditions.

(1) Campbell, C. T. The Degree of Rate Control: A Powerful Tool for Catalysis Research. ACS Catal. 2017, 7 (4), 2770–2779.

(2) Motagamwala, A. H.; Dumesic, J. A. Microkinetic Modeling: A Tool for Rational Catalyst Design. Chem. Rev. 2021, 121 (2), 1049–1076.

(3) Foley, B. L.; Bhan, A. Degrees of Rate Control at Non(Pseudo)Steady-State Conditions. ACS Catal. 2020, 10 (4), 2556–2564.