(467c) Designing the Protocols of Dynamic Catalysis

Enhancing the performance of heterogeneous catalytic reactors has been an area of active research: it can result in reduced costs and a smaller environmental footprint. Recent experimental capabilities enable the introduction of precisely controlled perturbations in heterogeneous catalytic reactors e.g. in terms of electrodynamic potential [1] or dynamic strain [2, 10]. These methods realize the ability to oscillate the binding energy of molecules on surfaces, leading to new possibilities for enhancing catalytic performance. It is long known that such dynamic operations, when appropriately designed, have the potential to improve catalytic performance by orders of magnitude over the static (or unperturbed) optimum [1, 3].

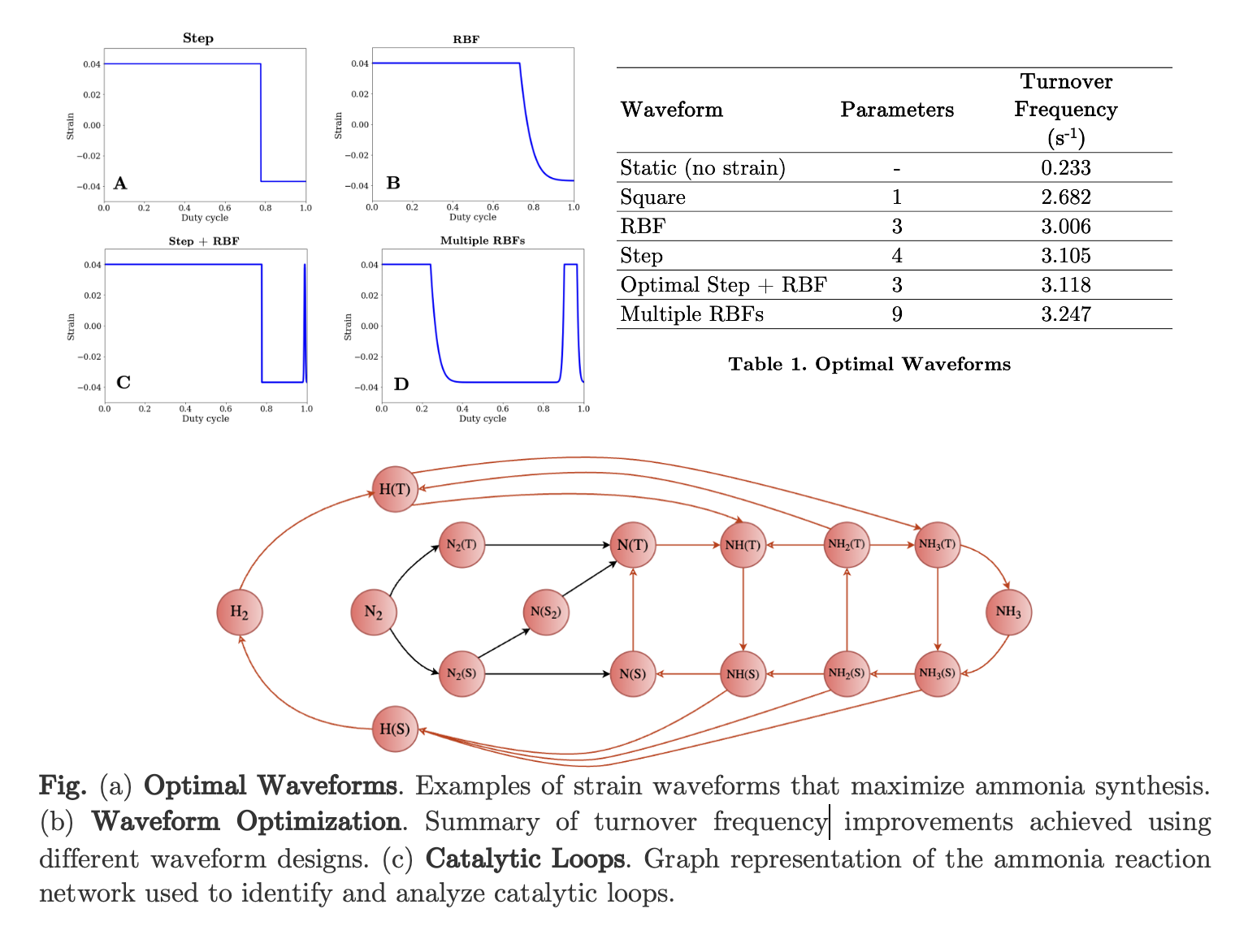
In this work we computationally discover optimal strain waveforms for dynamic ammonia catalysis on a ruthenium crystal perturbed using strain. We use a detailed, high-dimensional, microkinetic model [2] which considers different types of catalytic sites (such as terrace, upper steps, lower steps). Utilizing efficient scientific computing tools like matrix-free time-stepper-based solvers and Bayesian Optimization, [5] we demonstrate discovery of complex, optimal strain waveforms for ammonia synthesis. Our algorithmic pipeline is specifically designed to deal with detailed kinetic models (high-dimensional state space) and protocols of complex shape (high-dimensional parameter space). To solve for periodic steady states under varying waveforms, we demonstrate the benefits of Bayesian continuation, where we leverage an auxiliary Gaussian Process (GP) surrogate model [8] which is entirely dedicated to the solution space. Since the convergence of matrix-free time-stepper-based solvers for finding periodic steady states largely depend on initialization, our surrogate-guided continuation enables increasingly good predictions of initial guesses, substantially enhancing convergence. Bayesian continuation becomes a pivotal component in the active learning protocol for waveform optimization, enabling the design of dynamic strain programs that achieve industrial level catalytic performance under more affordable and sustainable conditions.

Introducing dynamic operation to heterogeneous catalytic reactions composed of intricate networks of elementary reactions with multiple pathways may create surface reaction loops where certain intermediate species cycle within a loop [6] reducing the overall yield of the desired products. To identify catalytic loops within this network, we represent the reaction network as a graph network, where reactions serve as vertices connected by edges. Using tools from graph theory [4], we investigate elementary catalytic loops embedded in these graph networks.

For the latter part of the study, we use a multi-fidelity approach to design optimal strain policies. Varying computational accuracy (and consequentially, computational cost), we constructed two distinct fidelity models. To further accelerate/improve the optimization scheme, we can also leverage the lower-fidelity model to gain useful information about the high-fidelity space while reducing the overall computational expense. By emphasizing the constructive interaction between the levels of fidelity, facilitated by multi-fidelity Gaussian Processes [7] and tailored acquisition functions [8, 9], we demonstrate the potential of multi-fidelity techniques in accelerating the discovery of optimal dynamic catalytic strategies.

To summarize, we developed a computational framework that integrates Bayesian optimization with a novel Bayesian continuation strategy to efficiently discover complex optimal strain waveforms for detailed microkinetic models, while ensuring robust solver convergence. We also perform a graph-theoretical analysis to investigate undesirable catalytic loops that may reduce catalytic performance. Additionally, we employ multi-fidelity Gaussian Processes to accelerate the discovery of optimal dynamic strain strategies by leveraging both high- and low-fidelity models, thereby reducing computational cost.

References

[1] M. A. Ardagh, M. Shetty, A. Kuznetsov, Q. Zhang, P. Christopher, D. G. Vlachos, O. A. Abdelrahman, and P. J. Dauenhauer, “Catalytic resonance theory: parallel reaction pathway control,” Chem. Sci., vol. 11, pp. 3501–3510, 2020.

[2] G. R. Wittreich, S. Liu, P. J. Dauenhauer, and D. G. Vlachos, “Catalytic resonance of ammonia synthesis by simulated dynamic ruthenium crystal strain,” Science Advances, vol. 8, no. 4, p. eabl6576, 2022.

[3] Y. M. Psarellis, M. E. Kavousanakis, P. J. Dauenhauer, and I. G. Kevrekidis, “Writing the programs of programmable catalysis,” ACS Catalysis, vol. 13, no. 11, pp. 7457–7471, 2023.

[4] D. B. Johnson, “Finding all the elementary circuits of a directed graph,” SIAM Journal on Computing, vol. 4, no. 1, pp. 77–84, 1975.

[5] B. Shahriari, K. Swersky, Z. Wang, R. P. Adams, and N. de Freitas, “Taking the human out of the loop: A review of bayesian optimization,” Proceedings of the IEEE, vol. 104, no. 1, pp. 148–175, 2016.

[6] M. A. Murphy, S. R. Gathmann, C. J. Bartel, O. A. Abdelrahman, and P. J. Dauenhauer, “Catalytic resonance theory: Circumfluence of programmable catalytic loops,” Journal of Catalysis, vol. 430, p. 115343, 2024.

[7] L. Le Gratiet and J. Garnier, “Recursive co-kriging model for Design of Computer experiments with multiplelevels of fidelity,” International Journal for Uncertainty Quantification, vol. 4, no. 5, pp. 365–386, 2014.

[8] K. Kandasamy, G. Dasarathy, and B. Póczos, “Multi-fidelity gaussian process bandit optimisation,” Journal of Artificial Intelligence Research, vol. 66, pp. 151–196, 2019.

[9] S. Guth, B. Champenois, and T. P. Sapsis, “Application of gaussian process multi-fidelity optimal sampling to ship structural modeling,” 34th Symp. on Naval Hydrodynamics, 2022.

[10] K. Yan, S. K. Kim, A. Khorshidi, P. R. Guduru, and A. A. Peterson, “High elastic strain directly tunes the hydrogen evolution reaction on tungsten carbide,” The Journal of Physical Chemistry C, vol. 121, no. 11, pp. 6177–6183, 2017