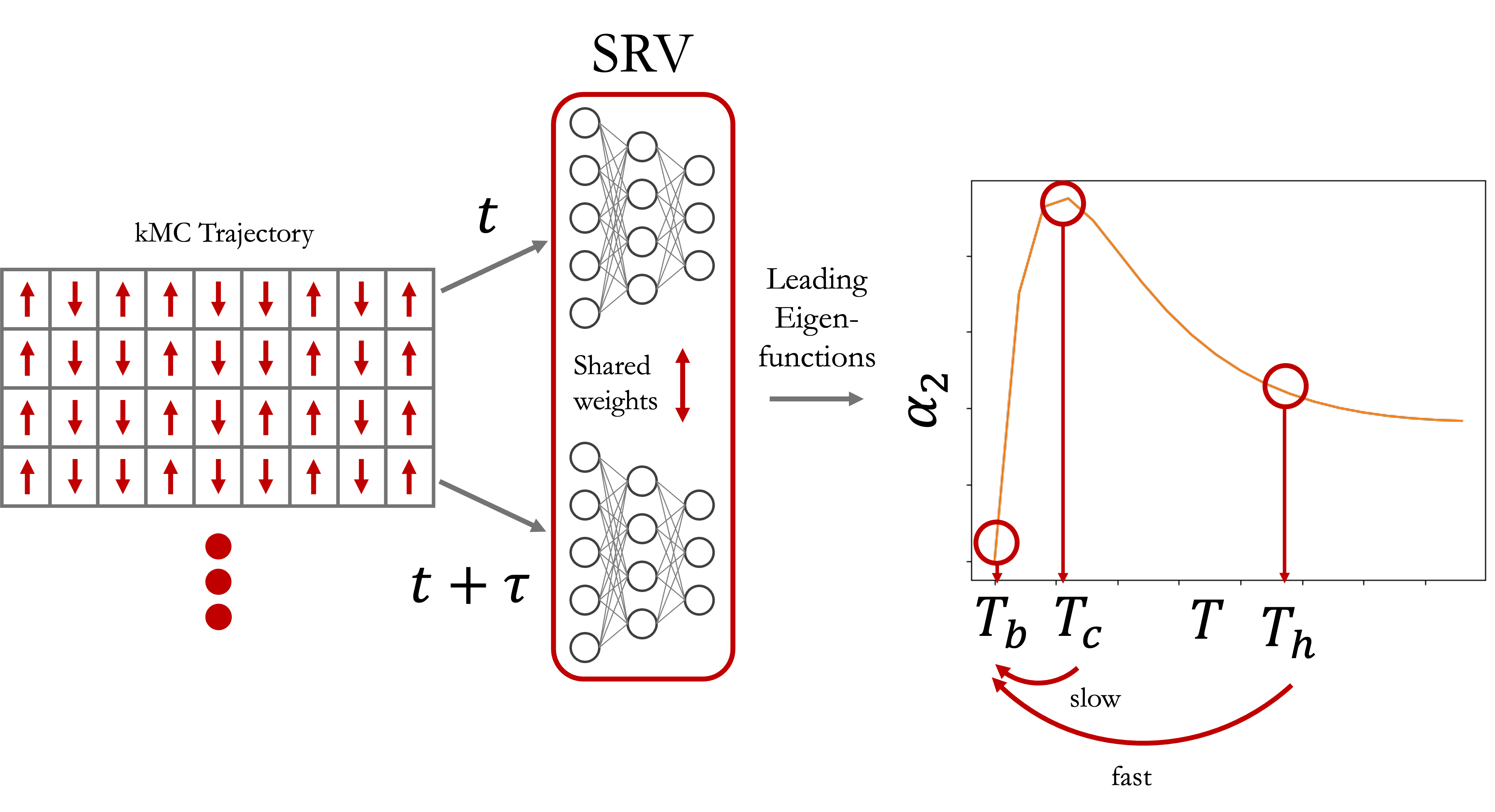
The Mpemba effect is commonly known as the phenomenon wherein hot water freezes faster than cold water. Reports of this effect date back to antiquity, but much controversy remains over claims of experimental observations of this effect. To be more precise, the (Markovian) Mpemba effect can be described as follows. Given three temperatures Tb<Tc<Th, the Markovian Mpemba effect is present if a system prepared in an equilibrium state at a high temperature Th relaxes to a new equilibrium with the bath at temperature Tb more quickly than a system prepared in an equilibrium state at the cool temperature Tc that is closer to the temperature of the bath. This behavior is often associated with the presence of metastable trapped states that, due to the topology and structure of the free energy landscape, the system prepared in the initially cool state experiences more strongly than the system prepared in the initially hot state. In this study, we develop a framework to identify the Markovian Mpemba effect for an arbitrary dynamical system by operating directly on trajectory data and without, as is usually necessary, requiring knowledge of the full rate matrix of the system. Specifically, we employ reversible VAMPnets (SRV), also known as deep time-lagged independent components analysis (Deep-TICA), to identify the relaxation modes of the system at Tb. We then detect the presence of the Markovian Mpemba effect by projecting the dynamics of the systems at Th and Tc onto the slowest relaxing mode and comparing the corresponding projection magnitude. If the system at Tc contains a larger projection weight on the slowest mode than the system at Th, then we prove that this is sufficient to verify the presence of the Markovian Mpemba effect. We demonstrate how our framework can successfully identify conditions for which the Markovian Mpemba effect is present in a simple 1D landscape containing a metastable trap, a 1D Ising model, and present some initial applications to molecular fluids.
