2025 AIChE Annual Meeting
(65k) Critical Conditions for the Onset of Electroconvective Instability Near an Ion-Selective Surface
Understanding and predicting the onset of EC instability is essential for improving performance in a wide range of electrochemical systems, including electrodialysis, capacitive deionization, and energy storage technologies. However, unlike classical bulk instabilities such as Rayleigh–Bénard convection, EC instability is highly localized and confined to the infinitesimal ESC region where a strong electric field exists. The multiscale and multiphysics nature of EC systems—combining nonlinear ion transport, electrostatics, and hydrodynamics in a spatially confined region—poses substantial challenges for both experimental and numerical investigations.
In this study, we present a comprehensive framework combining linear stability analysis (LSA) with scaling analysis to determine the onset of EC instability and elucidate the roles of electrolyte properties, membrane type, and operating conditions. The system under consideration consists of a binary electrolyte between an ion-selective membrane (cation- or anion-exchange) and a bulk reservoir, subjected to an applied voltage.
To understand ion transport, electrostatics, and hydrodynamics in the system, dimensionless forms of Navier-Stokes, Nernst-Plank, and Poisson equations are considered, and variables (e.g., velocities, ion concentrations and electric potential) in the governing equations are linearized to describe the base and perturbed status. The base equations are solved numerically to obtain steady-state profiles of ion concentration and electric potential.
From the base state solutions, we find that the majority of the applied voltage drop occurs within the ESC layer and that the electric field gradient undergoes a sharp transition at the ESC-bulk interface. Considering constant ion flux across both the bulk and ESC layer, we derive the ESC layer thickness LESC and interfacial potential at the bulk-ESC interface VESC, which are validated against 1D numerical simulations for different Debye lengths, ion valences, and membrane types. Our analysis confirms good agreement between our predictions and simulation results, and their scaling forms serve as the basis for predicting instability thresholds.
Next, the perturbation equations are solved as an eigenvalue problem, where the growth rate of disturbances is computed as a function of wave number and applied voltage. The results reveal that when the total system voltage is used as the control parameter, the neutral stability curves remain separated depending on the Debye length. However, when using only the potential drop across the ESC layer, these previously distinct curves collapse onto a single master curve, strongly indicating that the ESC-localized electric field governs the onset of instability.
We also examine the influence of ion transport properties. Higher counterion diffusivity leads to greater suppression of instability, as it enhances charge screening and reduces the net body force. For cation-exchange membrane (CEM), systems with higher cation diffusivity (e.g., KCl) require significantly higher critical voltages than systems with lower diffusivity (e.g., NaCl or NaOH). In contrast, anion-exchange membrane (AEM) exhibits the opposite trend, confirming the central role of counterion dynamics in setting the critical condition. These findings are in strong agreement with previous experimental observations [Kwak et al. (2013)] and provide theoretical grounding for diffusivity-based design strategies.
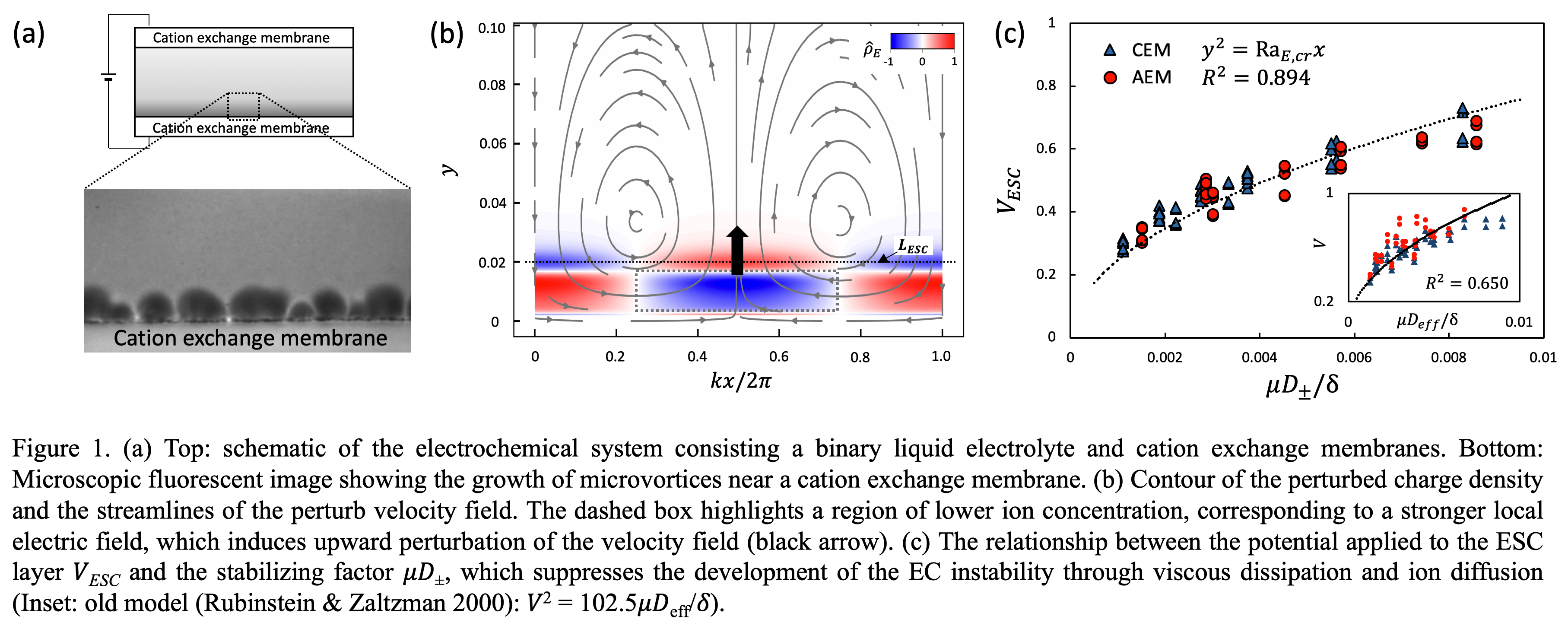
The spatial structure of the eigenfunctions reveals that perturbations in ion concentration, electric potential, and velocity are all strongly localized within the ESC layer. Two-dimensional visualizations show vortex-like flow patterns and perturbed charge density structures that mirror experimental electroconvection signatures (Figure 1a). The perturbed charge density within the ESC layer closely matches the distribution of the perturbed cation concentration. In the region highlighted by the dashed box in Figure 1(b), the local cation concentration is relatively low, indicating a reduced number of charge carriers. This leads to a locally higher resistance in that area, which in turn causes a comparatively stronger electric field to develop there. Consequently, this generates a perturbation velocity directed upward, as shown by the black arrow in Figure 1(b).
In this context, the onset of electroconvective instability is determined by the balance between the driving electric body force and the stabilizing effects of ion diffusion and viscous forces. This balance can be quantified by the electric Rayleigh number, 𝑅𝑎𝐸 = 𝛿𝑉ESC/𝜇𝐷±, where 𝑉ESC represents the potential drop across the ESC layer, 𝛿 is the permittivity, 𝜇 is the fluid viscosity, and 𝐷± is the diffusivity of the counterion. We then compare this formulation with the earlier model 𝑅𝑎𝐸,old = 𝛿𝑉ESC/𝜇𝐷eff [Rubinstein & Zaltzman (2000) and Li et al. (2022)], where 𝑉 is the total system voltage and 𝐷eff ≡ 2𝐷+𝐷−/(𝐷+ + 𝐷−) is the effective ion diffusivity (inset of Figure 1c), showing our model more accurately predicts the critical condition for instability.
This study offers an in-depth exploration of electroconvective (EC) instability in ion-selective systems, aiming to fill key gaps in understanding its onset and underlying mechanisms. Using scaling analysis, we estimated both the thickness of the extended space charge (ESC) layer and the potential drop across it, and confirmed these estimates through 1D ion transport simulations. Importantly, we emphasized that the potential drop across the ESC layer—not the total system voltage—is the relevant driving factor. Through linear stability analysis (LSA), we systematically investigated how ion valence, diffusivity, and bulk electrolyte concentration influence the critical conditions for instability. Our analysis of localized eigenfunctions revealed that the instability initiates within the ESC layer. Building on these insights, we introduced a universal scaling law and identified a critical electric Rayleigh number (RaE,cr = 60.4) that robustly predicts the onset of instability across different ion diffusivities and membrane properties. Collectively, these results advance our theoretical understanding of EC instability and provide practical guidance for improving the performance of ion-selective systems in electrochemical applications.
References:
Kwak, R., Guan, G., Peng, W.K. & Han, J. 2013 Microscale electrodialysis: Concentration profiling and vortex visualization. Desalination 308, 138–146.
Li, G., Townsend, A., Archer, L.A. & Koch, D.L. 2022 Electroconvection near an ion-selective surface with Butler–Volmer kinetics. J. Fluid Mech. 930, A26.
Rubinstein, I. & Zaltzman, B. 2000 Electro-osmotically induced convection at a permselective membrane. Phy. Rev. E 62, 2238.