(468b) Computing Lower Bounds More Efficiently in Dynamic Global Optimization

In certain chemical engineering applications such as safety verification, nonconvex optimization problems must be solved to guaranteed global ε-optimality in finite time. Typical methods for deterministic global optimization compute crucial lower bounding information by minimizing convex relaxations of objective functions. However, this lower bound evaluation may become computationally expensive if process models include embedded systems of ordinary differential equations (ODEs), since each single evaluation of an objective function’s convex relaxation nominally requires constructing and solving a separate ODE.

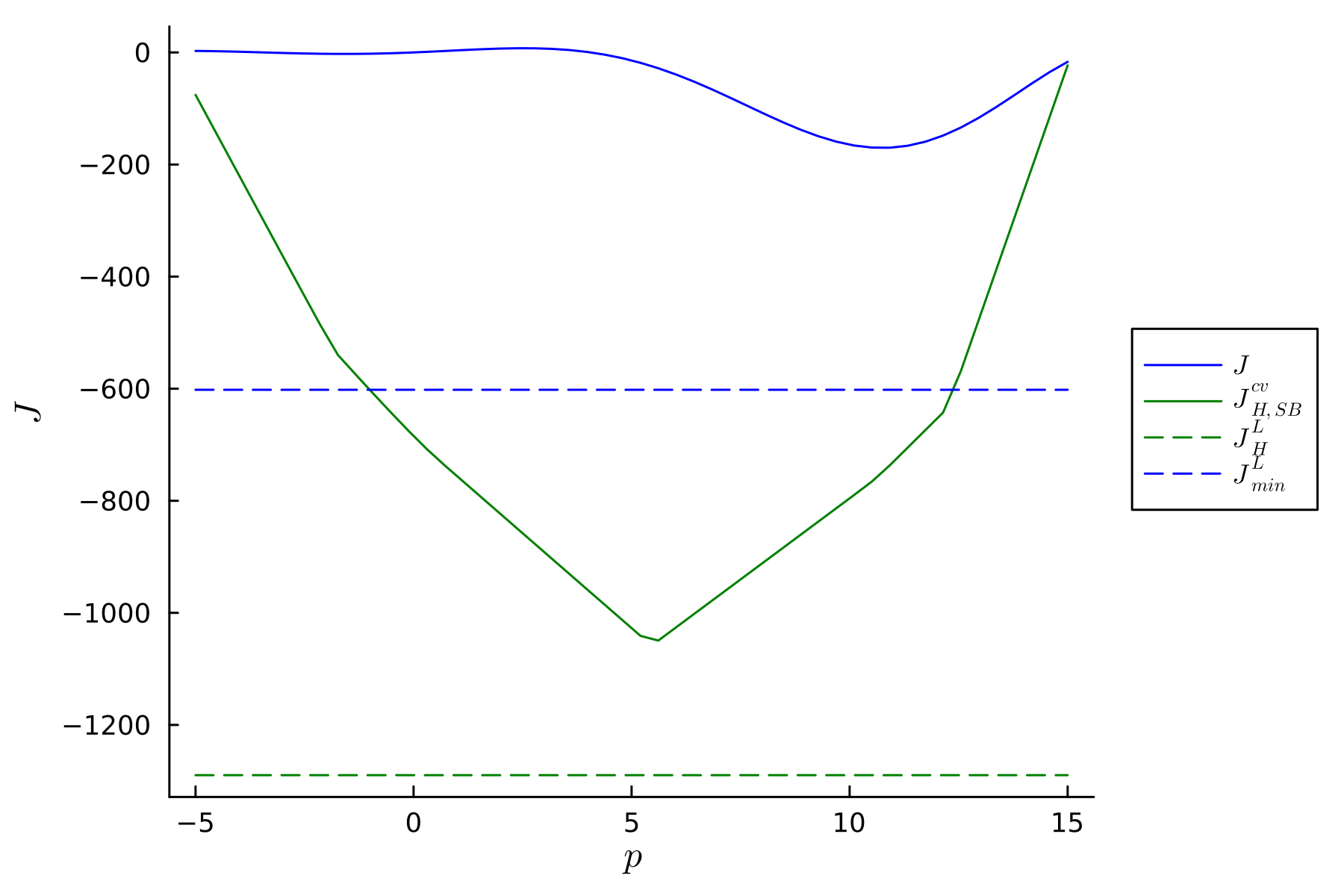
This presentation demonstrates two simple yet new and effective techniques to improve lower bound evaluation for dynamic global optimization. Firstly, we incorporate Tsoukalas and Mitsos’s composition relaxation rule [1] into the lower bounding formulation in a new way [under review]. The resulting formulation is guaranteed to tighten lower bounds compared to previous approaches based on generalized McCormick relaxations, without substantially affecting computational cost, and we show in several numerical examples that our new lower bounds are significantly greater. The attached figure shows our new lower bound (dashed blue) for a small nonconvex instance (solid blue), compared to bounds generated by two state-of-the-art approaches (bottom of the solid green curve, and dashed green). Secondly, we consider replacing convex relaxations of the ODE solution with affine relaxations produced according to our recent rigorous derivative-free relaxation procedure [2,3]. This approach will significantly reduce the number of ODE solves required to evaluate a correct lower bound, and we show in several numerical examples that comparable lower bounds are ultimately evaluated while significantly lowering computational cost. We suggest that both of these techniques should generally be employed when constructing lower bounds in global dynamic optimization, since they typically yield tighter, cheaper lower bounds.

References

[1] A Tsoukalas and A Mitsos, J. Glob. Optim., 2014. doi:10.1007/s10898-014-0176-0

[2] Y Song, H Cao, C Mehta and K Khan, Comput. Chem. Eng., 2021. doi:10.1016/j.compchemeng.2021.107413

[3] H-C Chui and K Khan, Proceedings of ADCHEM 2024. doi:10.1016/j.ifacol.2024.08.359