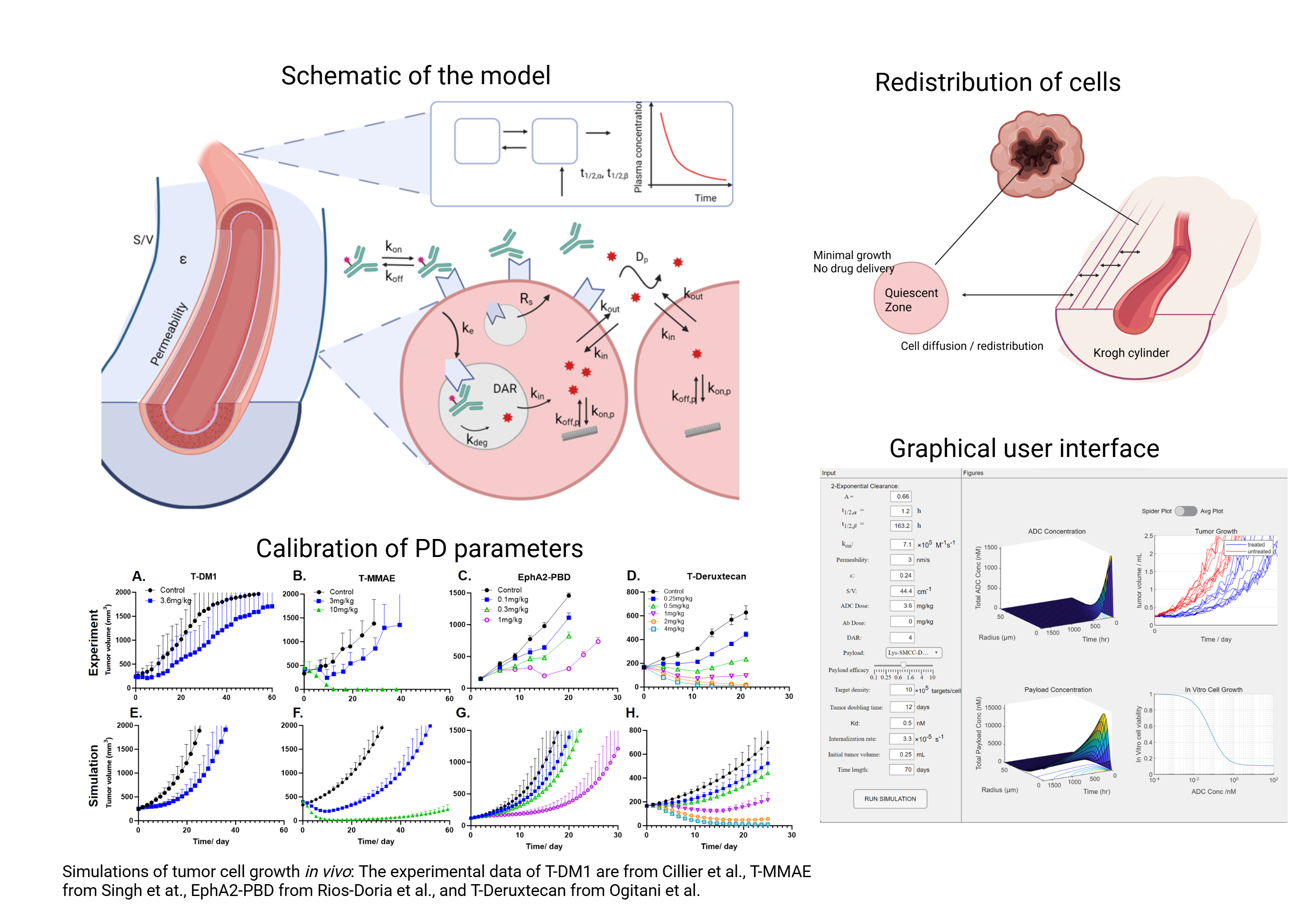
Our model successfully replicated both in vivo and in vitro experimental data collected from literature. Then we carried out clinical scaling of the model by incorporating detailed mechanisms of tumor cell growth, such as the quiescent zone around the necrotic core, tumor cell relocations, and potential clinical growth rates, to better capture ADC efficacy in patients. To make the model accessible to researchers who are not proficient in coding, a graphical user interface (GUI) was developed using MATLAB App Designer. Overall, the development of this model allows the generation of a widely available tool to predict ADC efficacy without the need for computing clusters.
The model captures both the detailed biodistribution of ADCs in solid tumor and the trend of plasma clearance in blood circulation, by integrating the Krogh cylinder model with two-compartment pharmacokinetics (PK). The Krogh cylinder simplifies the tumor geometry into cylinders of tumor tissue surrounding blood vessels. Partial and ordinary differential equations are formulated and solved using MATLAB. Tumor cell growth is estimated based on cell doubling time and the cytotoxic effects imposed by ADCs. A Michaelis-Menten equation is incorporated to relate the number of payloads bound to targets with the rate of cell death, while including a minimum concentration threshold of payloads needed to induce cell death. Pharmacodynamic (PD) parameters were calibrated for different payloads using in vitro cytotoxicity data as well as in vivo tumor growth trends.
Four ADCs are included in the simulations: T-DM1 (Kadcyla®), T-MMAE, EphA2-PBD and T-DXd (Enhertu®). In the four payloads simulated, MMAE, PBD and DXd have been reported to exhibit a bystander effect, showing considerable killing capacity to neighboring cells around tumor cells with target expression. The model captures this bystander killing by allowing lysosomally released payloads to leave the cytoplasm, diffuse through the membrane, and enter adjacent cells. Our previously published results have demonstrated that the co-administration of ADCs and carrier antibodies can enhance the efficacy of ADCs. Due to the large size of the antibody and elevated pressure in tumor tissue, the uptake of ADCs from plasma is extremely slow and difficult compared to antibody binding, resulting in ADCs primarily binding to perivascular targets before moving further. This heterogeneous distribution hampers the effective elimination of tumor cells by sparing cells farther from blood vessels. The addition of carrier antibodies improves the penetration of ADCs by competing for targets. Our computational model can also simulate the competition of binding sites between ADCs and antibodies, successfully replicating the experimental outcomes with enhanced efficacy.
To translate the validated model to the clinical setting, we incorporated additional mechanisms to better capture the complexities of clinical tumors. The tumor compartment is subdivided into quiescent cells, which no longer divide, and proliferating cells within Krogh cylinders. Tumor cells can redistribute between quiescent zones and Krogh cylinders or within Krogh cylinders when tumor cells are eliminated by ADCs and the surrounding environment changes. Evidence shows that equivalent drug doses are required to clear clinical tumors and mouse models, although tumors in the clinic generally exhibit a much slower growth rate. We propose a potential growth rate in the model, reflecting an underlying growth potential when tumor cells have sufficient nutrient supplies and space for division. With modest drug efficacy, this potential growth rate surpasses the clearance effects of ADCs, resulting in an unreduced growth rate limited by nutrients and space. Actual tumor shrinkage can only be observed when cell death induced by ADCs exceeds this potential growth rate. Incorporating the preceding mechanisms helps the model better capture the differences between mouse tumors and clinical tumors in addition to substituting human parameters. Simulation results are compared to tumor growth inhibition data collected in the clinic.
A GUI was developed encapsulating the calibrated PD parameters of the four payloads. The simulation of the model can be extended to other ADCs targeting different antigens beyond HER2, if the specific parameters are input. The use of computational modeling offers a cost-effective approach to investigate how some design parameters of ADCs, like target affinity or membrane permeability, influence the overall potency. It gives us a closer view of the relationship between ADC’s biodistribution in the tumor and drug efficiency. In conclusion, the model successfully replicated experimental outcomes and provided reasonable predictions of ADC efficacy in mouse models. We translated the validated model to the clinical setting by incorporating detailed tumor growth profiles. Additionally, we developed a GUI to package the code into a standalone application.