(289d) Blending in Baffled and Unbaffled Vessels in the Transitional Regime

In the turbulent regime, the dimensionless blend time, Nθ, measured in a baffled vessel is constant with the value of the constant dependent on the impeller type and its diameter relative to the vessel. As the viscosity increases the dimensionless blend time becomes inversely proportional to Reynolds number with the Reynolds number at the boundary between the turbulent and transitional regimes defined by [1]:

Re_B = 6400 / Po^1/3

Once the flow regime becomes transitional, the local blending rate measured near the impeller and in the batch is weakly dependent on Reynolds number, but the rate measured behind the baffle is strongly affected leading to the -1 exponent on Reynolds number. The local rate defines the overall rate for the whole batch[1].

Etchells and Hesketh have measured blend times in baffled and unbaffled vessels and found that the exponent on Reynolds number in the baffled vessel is -1.32 and -0.94 in the unbaffled vessel. The gradient for the baffled data is steeper (more negative) than the -1 which might be expected but there were differences in the experimental set up such as the vessel having a hemispherical base and the blend time being assessed by color change using the starch-iodine-sodium thiosulfate method. Even so, the removing the baffles reduced the blend time at a given Reynolds number and the divergence increases as the Reynolds number decreases.

This is an important result, especially for mixing processes operating in the transitional regime such as paint, personal products, such as shampoo, and foods, such as mayonnaise and ketchup.

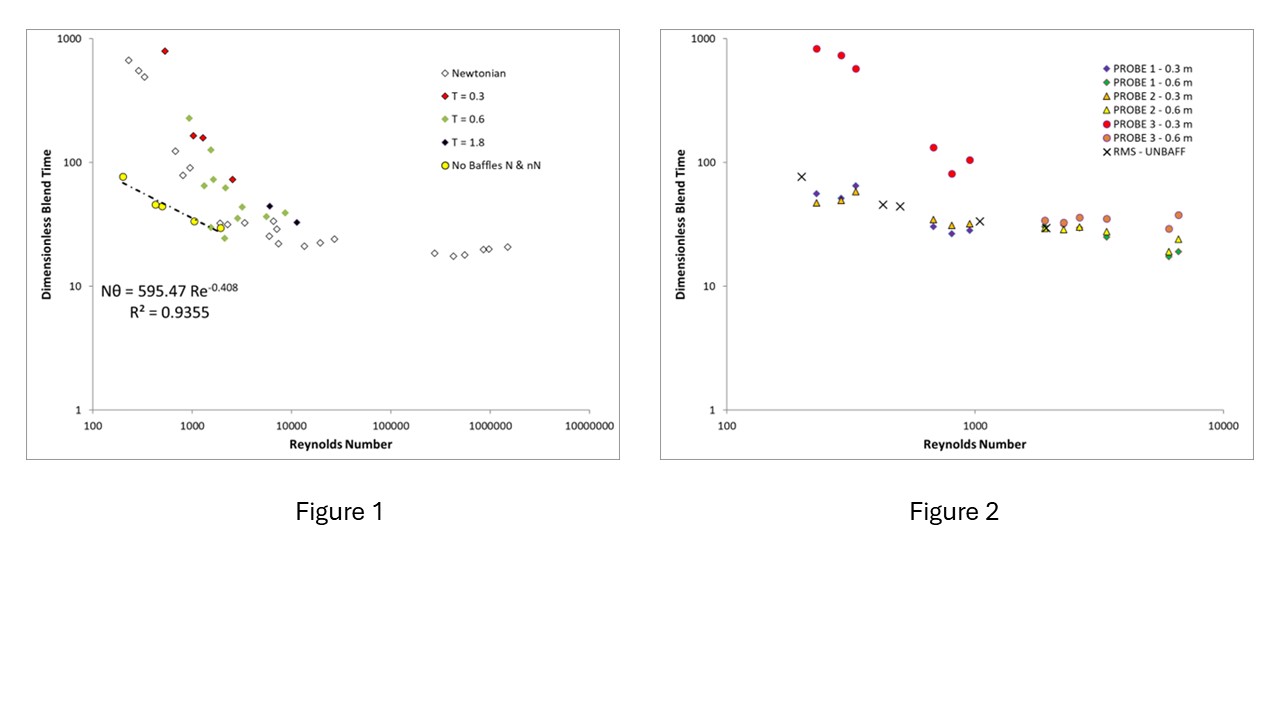
The Fluid Mixing Processes consortium has a very small sample of blend times measured in an unbaffled vessel with a T/2 diameter pitched-blade turbine. The vessel had a standard torispherical base with and without standard baffles. The data are plotted in Figure 1 with the open diamonds representing data measured with Newtonian fluids and the filled diamonds, non-Newtonian shear-thinning, analyzed using the Wall Shear Stress model[1]. The exponent on Reynolds number is -1 for the baffled data. The yellow circles represent data measured in the same vessel with the baffled removed.

In both FMP cases the exponents are larger (less negative) than those extracted from the Rowan data, and this could be due to the differences in the vessel and impeller geometries and the experimental method – color change versus conductivity.

Figure 2 shows the individual probe dimensionless blend times versus Reynolds number for the T/2 pitched blade turbine with the RMS blend times for the unbaffled case. This plot shows clearly that the presence of baffles in the transitional regime increases the blend time. The RMS blend time (representing the whole vessel) is the same as Probe 1 (beneath the impeller) and Probe 2 (halfway between the shaft and the vessel wall).

At the lowest Reynolds number, about 200, the dimensionless blend time is ~10 times shorter in the unbaffled case. But at the same Reynolds number and speed the power input is essentially the same – the Power numbers do not change significantly. So, for the same power input the blend time is 10 times shorter in the unbaffled case, but this difference reduces as Reynolds number increases until the Reynolds number at the transitional to turbulent boundary is reached.

Also, Hoogendoorn & Den Hartog [3] have shown that, once Re < 200, for turbines and the general recommendation is to consider using an impeller that is better suited to operating in viscous and non-Newtonian fluids such as a helical ribbon or Counterflow impellers. But it is probable that this limit is a result of the vessel being baffled, so would the range of Reynolds numbers where extend to lower values if the baffles are removed?

Nomenclature

N is the impeller rotational speed

Po is the impeller Power number

Re is the impeller Reynolds number

T is the vessel diameter

θ is the blend time

References

1. Grenville, R. K., “Blending of viscous Newtonian and pseudo-plastic fluids”, PhD Thesis, Cranfield Institute of Technology, 1992
2. Etchells III, A. W. & R. P. Hesketh, “Blending in unbaffled and baffled mechanically agitated vessels – effect of Reynolds number and liquid height”, ChERD, 196, 599-605, 2023
3. Hoogendoorn, C. J. & A. P. Den Hartog, “Model studies on mixers in the viscous flow region”, Chem. Eng. Sci., 22, 1698-1699, 1967