(584ac) Automatic Formulation and Exact Solutions to the Master Equation for Multisite Microkinetic Models in Catalysis

Microkinetic models (MKMs) have been widely used to describe adsorption, desorption, and reaction processes on heterogeneous catalyst surfaces by linking surface intermediate populations (coverages) to rate equations. These models predict surface coverages, state-to-state fluxes, overall reaction rates, reaction orders, rate-determining steps, and activation energies.

Mean-field MKMs assume negligible adsorbate-adsorbate interactions and provide closed-form rate laws, useful for hypothesis testing, data fitting, and reactor design. However, they lack the ability to describe surface diffusion or interactions between neighboring adsorbates. At the other extreme, kMC simulations, supported by ab initio data, handle atomistic surface details and complex reaction networks. While accurate, kMC requires extensive simulations and predefined rate parameters, making it less suitable for routine tasks like parameter estimation.

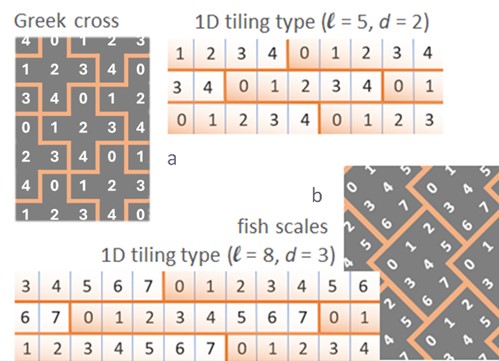
Emerging intermediate approaches, such as quasi-chemical models and closure approximations, address MF-MKM limitations but face challenges in generality and computational complexity. Our recent work introduced periodic tiling to simplify MKM formulation for small, symmetrical tiles, achieving accurate results for interacting adsorbates but with limitations for strong repulsions or diffusion.

This study presents a generalized method using extensible periodic tiles to model adsorption, reaction, diffusion, and desorption, providing results indistinguishable from kMC simulations under steady-state conditions.