2025 AIChE Annual Meeting
(390h) Application of Computer-Aided Molecular Design for Selecting Adsorbents to Isolate Nutraceuticals from Sugarcane
Authors
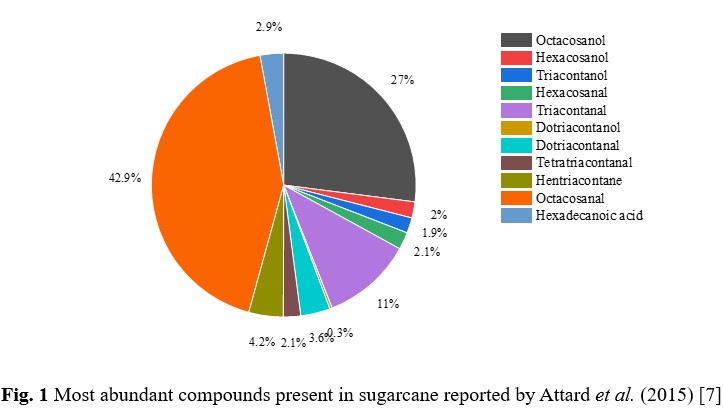
Nutraceuticals are natural health supplements obtained from food sources [1]. Octacosanol, one such example of nutraceuticals, is a straight-chain aliphatic fatty alcohol. It has many health benefits, including anti-Parkinsonism effect, improving endurance in athletes, anti-fatigue agent, etc. [2], [3], [4]. This fatty alcohol can be found in plant waxes like sugarcane, rice bran, soybean, wheat extract, etc., and animal waxes like beeswax [5]. Globally, India stands second, next to Brazil, in sugarcane production [6]. Sugarcane is rich in a vast range of compounds, namely, fatty alcohols, fatty acids, fatty aldehydes, fatty esters, etc., see Fig. 1 [7].
The system of compounds present in sugarcane is so diverse that we initially began separating the compounds using extraction. The selection of solvents plays an important role in the success of an extraction process. The research group has found the candidate solvents to extract octacosanol from the multi-component mixture using a computer-aided molecular design (CAMD) approach [8]. However, it has been observed that the selected solvent for the extraction dissolves other fatty alcohols along with octacosanol. Therefore, further purification of the extract containing octacosanol is needed, which can be done using adsorption.
Adsorption
Adsorption is one of the most widely used separation techniques in industries, though it is more expensive than other commonly used methods, such as distillation [9]. It becomes a more economical option if the relative volatility decreases, increasing the efficiency of separating a desired compound from a mixture [9]. Therefore, separating octacosanol from the rest of the fatty alcohols using adsorption can be a viable technique because the group of fatty alcohols, known as policosanols, differ in the number of carbon atoms only, and may behave similarly to each other, i.e., homologous series of compounds. Applications of adsorption also include the purification of gas and liquid mixtures, isomer separations, removal of impurities from air and water, pharmaceutical purification, and many more [9].
In adsorption, selecting adsorbents is as important as solvent selection in an extraction process. Generally, this is done using two conventional approaches: experimentation and screening the properties database. However, such approaches cannot provide an exhaustive solution. In this study, we developed a CAMD problem for designing optimal adsorbents to isolate octacosanol from the rest of the policosanols. Similar to the group contribution method (GCM) model, UNIFAC, used in solvent selection [10], the model used for adsorption is adsorbate solid solution theory. The following section discusses this theory in detail.
GCM for octacosanol adsorbents
The adsorbate solid solution theory (ASST) describes the behaviour of fluid molecules (adsorbates) on a solid surface (adsorbent), treating the adsorbed phase as a solid solution rather than a distinct separate phase [11]. This theory helps to understand how different structural groups of adsorbates interact with each other and the solid surface, especially in multicomponent adsorption systems. The interactions can be estimated using excess Gibbs free energy (GE) models, i.e., the activity coefficient values in the bulk (γb) and surface phases (γs) are calculated. These values help to find the phase equilibrium relation for each component on the adsorbent. The equilibrium relation for a component i whose mole fraction is x is as shown Eq. 1, [11]:
xbiγbi = xsiγsiexp((gad-gad0i)/RTΓsmi (1)
Where gad is the free energy of immersion in the adsorbed solution, and gad0i is the free energy of immersion in the pure adsorbed species. R is the ideal gas constant, T is the temperature in Kelvin, and Γsmi is the surface phase capacity of each adsorbent. In Eq. 1, the activity coefficients can be calculated using the modified UNIFAC group contribution method model, where the activity coefficients are functions of van der Waals surface area (Ri) and volume (Qi) of each functional group and the interaction parameters, amn, between two groups as shown in Eq. 2:
γi = f(Ri, Qi, R, T) (2)
For the sake of brevity, we referred to Fredenslund et al. (1977) [12] for details of equations embedded in Eq. 2, as these equations are the same for solid-liquid or vapor-liquid equilibria. These interaction parameters for groups can be calculated from known compounds' adsorption curves by using the following optimization problem.
min Err = min (Σad1Σeq1 (qexp - qcal))2 (3)
Where q is the adsorption capacity of the adsorbent, and can be calculated using Eq. 1.
Once the interaction parameters present in the ASST are known, using those functional groups, we can build an optimization problem to design adsorbents [13], [14]. CAMD is a reverse of GCM.
CAMD for adsorbents for Octacosanol
CAMD has been extensively used in applications, namely, designing solvents, polymer designs, refrigerant designs, catalysts, value-added products, and foaming agents. However, this is the first time such an approach has been proposed for extracting a nutraceutical from biomass. The problem of adsorbent for the separation process can be posed mathematically as an optimization problem, as shown in Eq. 4:
Maximize q Adsorption Capacity for adsorbent design (4)
subject to
Eb,L ≤ Eb ≤ Eb,U Binding Energy Constraint for Chemical Stability of adsorbents
ΣiΣjVi,j ≤ ε Structural Constraint
where q is the adsorption capacity of the adsorbent, is the binding energy which is linked to Gibbs’ free energy, is the valency of a functional group and is the number of times it appears in the designed molecule. The bounds (for the property) are denoted by subscript L for the lower bound and U for the upper bound, respectively.
Efficient Ant-Colony Optimization
A combinatorial optimization problem can be solved using an ant colony optimization (ACO) algorithm or any other metaheuristic approaches like simulated annealing and genetic algorithm [15]. On the other hand, there has been a significant expansion in the field of study to apply this technique to non-linear situations with continuous and mixed variables. A study reported the development of ACO using Hammersley sequence sampling to solve such optimization problems [15]. Briefly, the behaviour of actual ants searching for food was bio-modelled in order to create the ACO algorithm. An ant returns to its starting position after releasing a chemical known as a pheromone along the way. The other ants would be able to find their way to the food source with the same assistance. Many paths would exist, and as time passes, the concentration of pheromones on less-travelled paths evaporates. This leads to finding shorter paths, and eventually, the shortest path would be found.
Expected Results
As mentioned earlier, octacosanol was still not achieved using the extraction process alone. Therefore, we need to estimate the interactions between the groups of octacosanol and those of the adsorbent. But there is no literature available on the adsorption of octacosanol or even policosanols. Nevertheless, we can estimate the interaction parameter values between the functional groups of butanol (and other similar compounds) and those of the adsorbent reported in the literature [16], using the above-mentioned equations and derive the GCM for octacosonal. This is because both butanol and policosanols contain the same functional groups, i.e., CH3–, –CH2–, and –OH, and hence, the estimation of interaction parameters and subsequently, the activity coefficient values between these functional groups and those present in the solid phase can be found. Based on these activity coefficient values, the CAMD approach facilitates the design of optimal adsorbents and may facilitate the isolation of octacosanol from the other policosanols. In the future, we will experimentally verify these adsorbents for the separation of octacosanol.
References
[1] E. K. Kalra, “Nutraceutical - Definition and Introduction,” AAPS PharmSci, vol. 5, no. 3, p. 25, 2003, doi: 10.1208/ps050325.
[2] Y. Zhou, F. Cao, F. Luo, and Q. Lin, “Octacosanol and health benefits: Biological functions and mechanisms of action,” Jun. 01, 2022, Elsevier Ltd. doi: 10.1016/j.fbio.2022.101632.
[3] R. Sharma et al., “Octacosanol and policosanol prevent high-fat diet-induced obesity and metabolic disorders by activating brown adipose tissue and improving liver metabolism,” Sci Rep, vol. 9, no. 1, Dec. 2019, doi: 10.1038/s41598-019-41631-1.
[4] S. Sen Gupta and M. Ghosh, “Octacosanol educes physico-chemical attributes, release and bioavailability as modified nanocrystals,” European Journal of Pharmaceutics and Biopharmaceutics, vol. 119, pp. 201–214, Oct. 2017, doi: 10.1016/j.ejpb.2017.06.020.
[5] S. Irmak, N. T. Dunford, and J. Milligan, “Policosanol contents of beeswax, sugar cane and wheat extracts,” Food Chem, vol. 95, no. 2, pp. 312–318, Mar. 2006, doi: 10.1016/j.foodchem.2005.01.009.
[6] N. Ungureanu, V. Vlăduț, and S. Ștefan Biriș, “Sustainable Valorization of Waste and By-Products from Sugarcane Processing,” Sep. 01, 2022, MDPI. doi: 10.3390/su141711089.
[7] T. M. Attard, C. R. McElroy, C. A. Rezende, I. Polikarpov, J. H. Clark, and A. J. Hunt, “Sugarcane waste as a valuable source of lipophilic molecules,” Ind Crops Prod, vol. 76, pp. 95–103, Dec. 2015, doi: 10.1016/j.indcrop.2015.05.077.
[8] Nistala Venkata Subrahmanyam, Sharad Bhartiya, Vinay A Juvekar, and Urmila M Diwekar, “662e - Optimal Solvent Selection Using Computer-Aided Molecular Design (CAMD) to Obtain Octacosanol from Sugarcane Rind,” AIChE 2024 Annual Meeting.
[9] D. M. Ruthven, Principles of adsorption and adsorption processes. John Wiley & Sons, 1984.
[10] K. J. Kim and U. M. Diwekar, “Efficient combinatorial optimization under uncertainty. 2. Application to stochastic solvent selection,” Ind Eng Chem Res, vol. 41, no. 5, pp. 1285–1296, Mar. 2002, doi: 10.1021/ie0101691.
[11] C. Berti, P. Ulbig, A. Burdorf, J. Seippel, and S. Schulz, “Correlation and prediction of liquid-phase adsorption on zeolites using group contributions based on adsorbate-solid solution theory,” Langmuir, vol. 15, no. 18, pp. 6035–6042, Jan. 1999, doi: 10.1021/la981415p.
[12] A. Fredenslund, J. Gmehling, and P. Rasmussen, Vapor-liquid equilibria using UNIFAC : a group contribution method. Elsevier Scientific Pub. Co., 1977.
[13] R. K. Doshi, R. Mukherjee, and U. M. Diwekar, “Application of Adsorbate Solid Solution Theory to Design Novel Adsorbents for Arsenic Removal Using CAMD,” ACS Sustain Chem Eng, vol. 6, no. 2, pp. 2603–2611, Feb. 2018, doi: 10.1021/acssuschemeng.7b04094.
[14] M. Shahmohammadi, R. Mukherjee, C. G. Takoudis, and U. M. Diwekar, “Optimal design of novel precursor materials for the atomic layer deposition using computer-aided molecular design,” Chem Eng Sci, vol. 234, Apr. 2021, doi: 10.1016/j.ces.2020.116416.
[15] U. Diwekar and B. Gebreslassie, “Efficient ant colony optimization (EACO) algorithm for deterministic optimization,” International Journal of Swarm Intelligence and Evolutionary Computation, vol. 1, 2016, doi: 10.4172/2090-4908.1000131.
[16] F. Raganati, A. Procentese, G. Olivieri, M. E. Russo, P. Salatino, and A. Marzocchella, “Bio-butanol separation by adsorption on various materials: Assessment of isotherms and effects of other ABE-fermentation compounds,” Sep Purif Technol, vol. 191, pp. 328–339, 2018, doi: 10.1016/j.seppur.2017.09.059.