(11c) Adaptive Sampling for Robust Process Design Under Uncertainty

Designing a process comprises several key steps, from problem definition and initial hypothesis formulation to experimental design, modelling, optimization, process improvement, and more. Uncertainty is found at any of these steps and more specifically in the initial phases. For this reason, process design is inherently an iterative process. The key to an effective and efficient process design is to reduce such uncertainty and maximize the information gathered from the physical system, through experimentation and modelling.
One strategy to tackle this challenge is adaptive sampling, which is a strategy that aims to maximize the knowledge gathered from a design of experiments (DoE) campaign for building more accurate systems models [1].

In process development, where accurate modelling is not available a priori, controlling uncertainty in the fundamental steps of experimental design and modelling itself might be challenging. The most recognized technique for adaptive sampling is arguably Bayesian optimization [2, 3]. In Bayesian optimization, a surrogate model is built and paired with an acquisition function to guide the sampling strategy.
Formulating a well-designed acquisition function is highly problem-specific, and the nature of Bayesian optimization makes it generally difficult to parallelize, given the need to update the surrogate at each adaptive iteration [4]. Balancing exploration and exploitation also adds another layer of complexity [5].
Moreover, when uncertainty in the adopted surrogate model or the experimental data itself translates to poor predictive accuracy on the target physical system, applying such a strategy effectively becomes problematic. The main challenge in these cases, where model uncertainty and bias are present, is preventing the model from negatively impacting the resulting adaptive DoE. The potential effect would be reducing the system information extracted by, e.g., forming clusters of samples too close to one another.
Ensuring uniformity and space-fillingness throughout the adaptive sampling iterations can curb the effect of such model bias in the resulting DoE.

In this work, we propose a methodology for adaptive sampling that is natively uniformly structured and space-filling, less prone to surrogate model bias, easily parallelizable, with no acquisition function formulation, and agnostic regarding the surrogate model implied.
The methodology ensures structure and space-fillingness by relying on Delaunay triangulation, thus curbing model uncertainty in the resulting DoE.
The methodology is applied to three-dimensional problems using probabilistic surrogate modeling that accounts for experimental uncertainty. At each iteration, the volumes of simplices generated via Delaunay triangulation are calculated, and the next adaptive sample is placed at the centroid of the selected three-dimensional simplex.
The samples thus gathered are then used to update the probabilistic surrogate model, which in turn guides the next adaptive iteration.
The methodology can also be easily parallelized by selecting multiple simplices at each adaptive iteration, thus generating a batch of new adaptive sampling points.
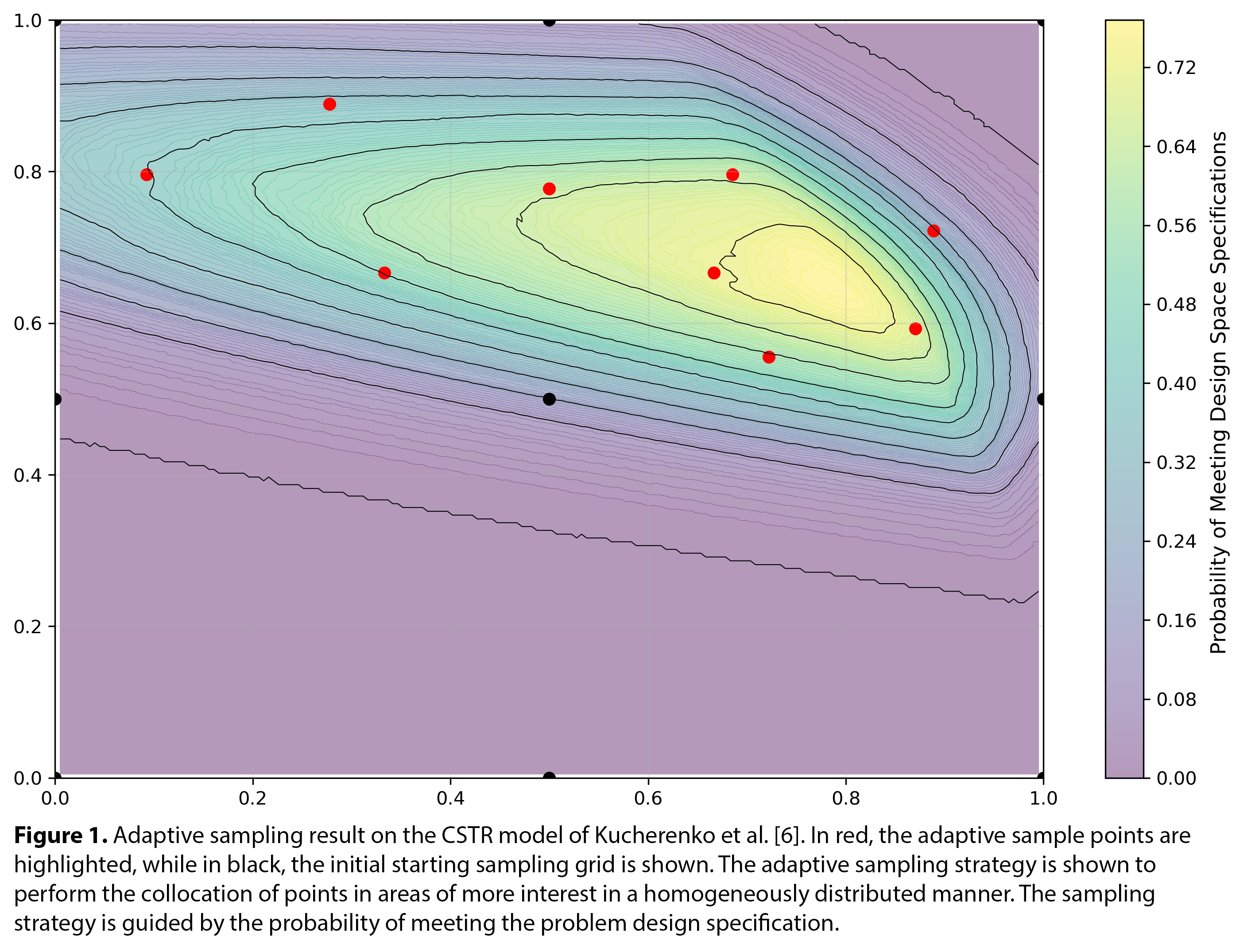
The methodology is demonstrated on the CSTR reactor problem presented by Kucherenko et al. [6], where the mechanistic model serves as an in-silico experimentation platform to evaluate its performance. Compared to traditional sampling techniques, the proposed approach achieves higher modelling accuracy with fewer samples, while also addressing common limitations associated with Bayesian optimization-based adaptive sampling strategies.

Acknowledgments

Funding from the UK Engineering & Physical Sciences Research Council (EPSRC) for the i-PREDICT:Integrated adaPtive pRocEss DesIgn and ConTrol (Grant reference: EP/W035006/1) is gratefully acknowledged.

References

[1] Bhosekar, A., & Ierapetritou, M. (2018). Advances in surrogate-based modeling, feasibility analysis, and optimization: A review. Computers & Chemical Engineering, 108, 250–267. https://doi.org/10.1016/j.compchemeng.2017.09.017

[2] Boukouvala, F., & Ierapetritou, M. G. (2012). Feasibility analysis of black-box processes using an adaptive sampling Kriging-based method. Computers & Chemical Engineering, 36, 358–368. https://doi.org/10.1016/j.compchemeng.2011.06.005

[3] Liu, H., Ong, Y.-S., & Cai, J. (2018). A survey of adaptive sampling for global metamodeling in support of simulation-based complex engineering design. Structural and Multidisciplinary Optimization, 57(1), 393–416. https://doi.org/10.1007/s00158-017-1739-8

[4] Geremia, M., Bezzo, F., & Ierapetritou, M. G. (2023). A novel framework for the identification of complex feasible space. Computers & Chemical Engineering, 179, 108427. https://doi.org/10.1016/j.compchemeng.2023.108427

[5] Kudva, A., Tang, W.-T., & Paulson, J. A. (2024). Robust Bayesian optimization for flexibility analysis of expensive simulation-based models with rigorous uncertainty bounds. Computers & Chemical Engineering, 181, 108515. https://doi.org/10.1016/j.compchemeng.2023.108515

[6] Kucherenko, S., Giamalakis, D., Shah, N., & García-Muñoz, S. (2020). Computationally efficient identification of probabilistic design spaces through application of metamodeling and adaptive sampling. Computers & Chemical Engineering, 132, 106608. https://doi.org/10.1016/j.compchemeng.2019.106608