(291d) 3D Dynamics of Vibro-Fluidized Beds Revealed By Magnetic Resonance Particle Tracking

Even though granular matter is athermal, when it is externally driven it fluidizes and behaves similarly to classical matter [1]. Fluidization is used in many industrial processes such as catalysis and carbon capture [2]. Gaining a deeper understanding of how fluidization behaves under different conditions, along with the mixing dynamics of fluidized beds, is essential for improving these applications. When properly fluidized, granular matter exhibits diffusion, ensuring efficient mixing. However upon increased compression, particles become less mobile and collective effects become more important, hindering mixing and approaching a disordered solid structure [3]. This phenomenon is still poorly understood and calls for means to track individual particles in order to capture its underlying mechanisms at the most fundamental level.

Recently, we developed a novel measurement technique based on nuclear magnetic resonance that is able to track particles in 3D granular systems [4], dubbed Magnetic Resonance Particle Tracking (MRPT). Unlike imaging techniques that obtain information at the density level, MRPT can recover full trajectories of many particles simultaneously at the micron and millisecond level.

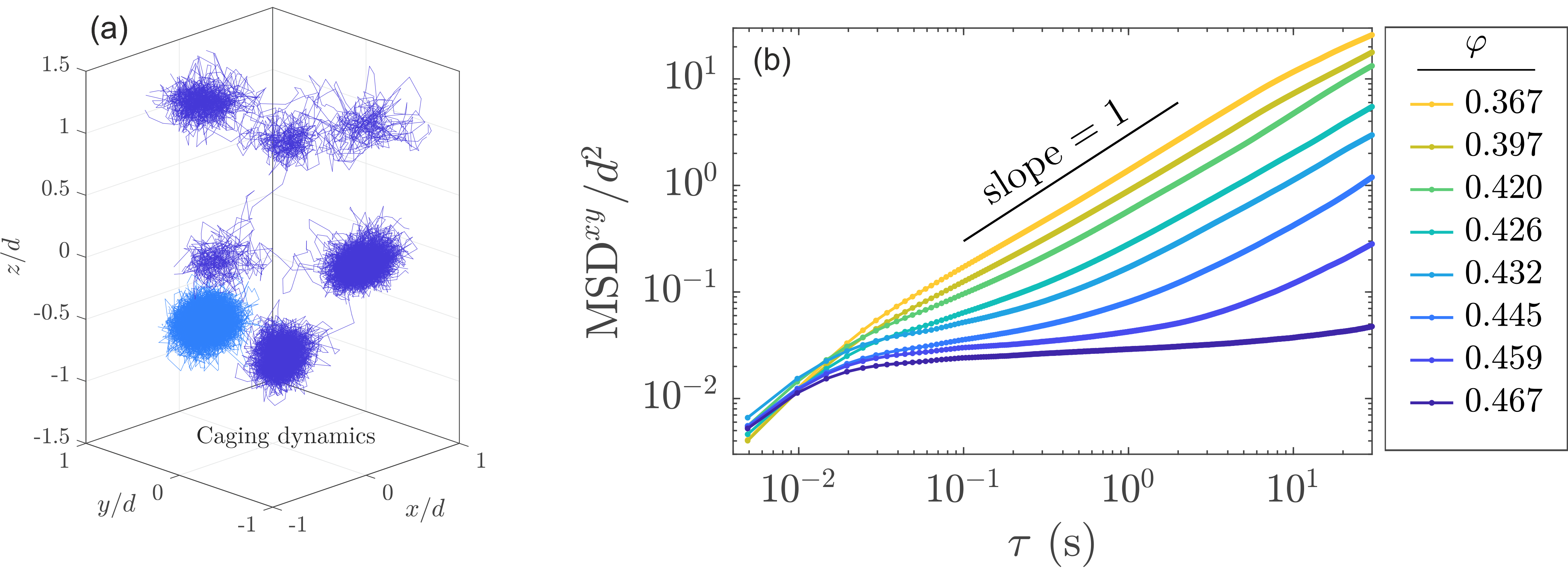
In this work, we leverage the capabilities of MRPT to investigate the 3D dynamics of a vibro-fluidized bed at various volume fractions. For low volume fractions, we observe diffusive behavior of the particles characterized by a linear time dependency of the mean squared displacement. As the volume fraction is increased, the particle dynamics slow down and individual grains become trapped by their neighbors, a phenomenon known as caging [2]. This process eventually breaks the ergodicity of the system and the bed cannot mix properly anymore. Thanks to the high spatiotemporal resolution of MRPT, we can capture these caging dynamics precisely (Fig. 1a). We identify the time scales and volume fractions at which this phenomenon occurs, providing direct insight into the duration of the system’s structural memory (Fig. 1b). This, in turn, serves as a measure of the mixing efficiency.

References

[1] H. M. Jaeger, S. R. Nagel, and R. P. Behringer, Rev Mod Phys 68, 1259 (1996).

[2] D. Kunii and O. Levenspiel, Fluidization engineering (Elsevier, 2013).

[3] K. Binder and W. Kob, Glassy Materials and Disordered Solids: An Introduction to their Statistical Mechanics (World Scientific, 2011).

[4] M. Suter, J. P. Metzger, A. Port, C. R. Müller, and K. P. Pruessmann, (2025), p. arXiv:2503.22425.

Figure 1. (a) Particle trajectories reveal dynamics such as caging. (b) The mean squared displacement shows diffusive behavior for low volume fractions .