Breadcrumb
- Home
- Publications
- Proceedings
- 2024 AIChE Annual Meeting
- Poster Sessions
- General Poster Session
- (735aq) Upscaling of Lithium-Ion Battery Models: From the Pore-Scale to the Cell- Scale through Homogenization.

There is a continued interest in the development of mathematical models that can efficiently and accurately describe the behavior observed during lithium-ion battery operation. Such models are often based on a simplified description of the electrochemical behavior because the morphological characterization of the electrode is complex and expensive from a computational point of view. However, batteries often exhibit non-uniform behavior in the current distribution, which can adversely affect battery performance, utilization, and lifetime. One of the aspects that is more responsible for this non-uniformity is the electrode morphology. Indeed, one of the limitations of the most common models that are present in literature is that each particle is reconstructed with a spherical shape. And if this approximation should be acceptable for the cathode side, the same can not be said for the anode side which is composed of graphite. This carbon form, which is the most stable one, is an anisotropic material because atoms are arranged in a hexagonal pattern forming a layer structure that makes graphite a good electric and heat conductor. Due to the layer structure, graphite particles have a flake shape, with one characteristic dimension smaller than the other two. The geometrical shape of graphite has a crucial impact on the whole electrochemical process involved in a lithium-ion battery and the correct reconstruction in-silico of the microscopic electrode geometry is fundamental to correctly understand the charge and discharge process from a macroscopical point of view [2].
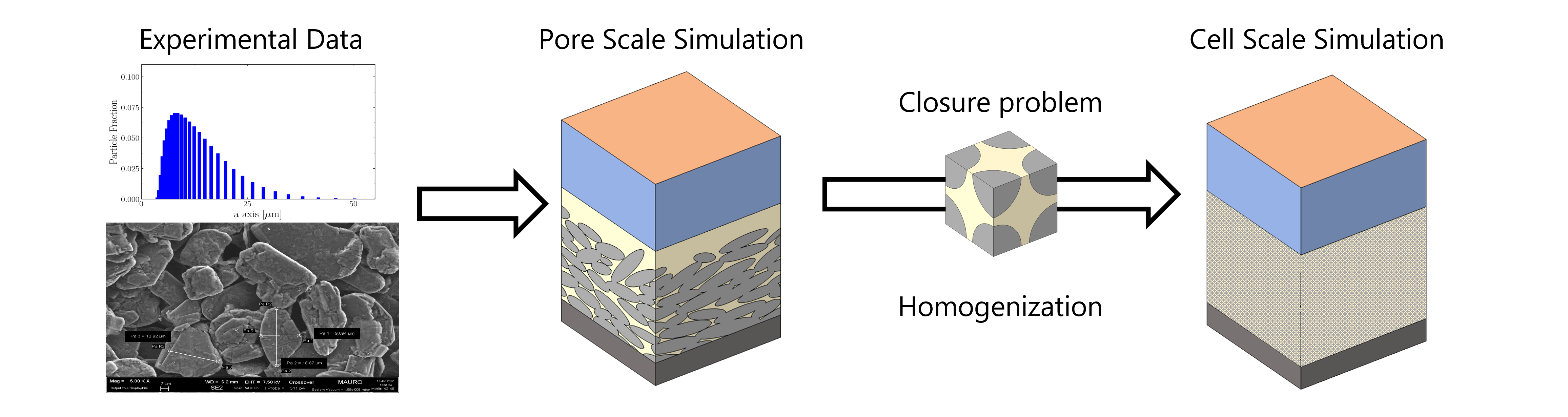
Under these conditions, we decided to focus our attention on the geometrical characterization of the electrode of a graphitic half-cell. The main idea of this work is to start from a microscopic detailed model of a half-cell to obtain an upscaled model via homogenization techniques to speed up the simulation. This fast prediction is crucial to study in a short time different types of electrodes with a low computational cost.
To start, it was necessary to choose a way to reproduce graphite particles. To do this, we started looking for a geometric shape that met several requirements. The shape should be a compromise between accuracy and computational cost. An extremely realistic representation, leading to an equally highly complex electrode geometry, would be very difficult to recreate, owing to the necessity of using computationally expensive geometric algorithms, and it would also lead to expensive battery simulations. On the other hand, using too simplified of a model (e. g. spheres as previously mentioned) would lead to an unacceptably unrealistic electrode representations, impacting the quality of the simulation results. After these considerations, we decided to adopt an ellipsoidal shape for the particles. Each particle is characterized by a semi-axis much shorter than the other two. The two larger characteristic lengths are taken from particle size distribution (PSD) data obtained in laboratory tests, together with an evaluation of the particles aspect ratio from SEM image analysis. In this way, we were able to obtain a good representation of the electrode geometry, and this was confirmed by the experimental evaluation of the porosity. The packing of ellipsoids was produced with a combination of two Python based open-source codes. The first one is Yade-DEM and we used it to generate a package of spheres starting from the experimental PSD. Later, each sphere was transformed into a flattened ellipsoid with the software Blender. Then, a rigid-body simulation was conducted to compact the layer of particles and to remove the empty space formed after the transformation of each sphere. Finally, the central portion of the package was extracted and used as input to setup the pore-scale simulations, performed with the software COMSOL 6.1. This whole process is governed by a Python script that allows us to produce different electrodes in a semi-automatic way.
The same script was also used to create the model used for the homogenization process. In this case there are some important conditions that should be respected. The main idea of homogenization is to find the macroscopic properties by investigating microscopical behavior. This upscaling is possible thanks to the multiple-scale expansion. This technique consists in rewriting the equations in a dimensionless form to extract, in this case, the Damköhler number and the Péclet number. These two parameters define the condition in which there is scale separation and the possibility of homogenizing microscopic equations. Then, the solution of a closure problem on a periodic cell is necessary to obtain the upscaled effective values for both the diffusivity coefficient and the electrical conductivity for the liquid and solid phases [3-4]. The closure problem is solved on a unitary periodic cell that has a dimension many times smaller than the pore-scale model, providing for a microscopic representative volume. For the case under consideration, the unitary cell has been created with a central core of polydisperse ellipsoids, and a few semi-ellipsoids arbitrarily placed on the boundaries to respect the unit cell periodicity. Once obtained the effective values for the diffusion coefficient and for the electrical conductivity, is possible to create and solve the homogenized model.
The results extracted from the homogenized model are then compared and validated with the ones obtained from the 4D pore scale simulation. With the homogenized model we can obtain the same results as the pore scale model but in shorter times and less computational resources. With the script created for the electrode geometry, we can obtain different morphologies and particles size distribution. The flexibility of the model, coupled with the possibility of studying the behavior of different electrodes, will allow for the easy creation of a large dataset on a wide parameter space, to be used as training data for a neural network model, used a quick surrogate model to expand the range of explorable electrode configurations.
[1] McKinsey & Company, (2023), Battery 2030: Resilient, sustainable, and circular, https://www.mckinsey.com/industries/automotive-and-assembly/our-insights/battery-2030-resilient-sustainable-and-circular
[2] Lu, X., Lagnoni, M., Bertei, A. et al., (2023), Multiscale dynamics of charging and plating in graphite electrodes coupling operando microscopy and phase-field modelling. Nat Commun 14, 5127.
[3] Arunachalam, H., Onori, S., Battiato, I., (2015), On Veracity of Macroscopic Lithium-Ion Battery Models. J. Electrochem. Soc., 162, A1940
[4] Ling, B., Battiato, I., (2020), τ-SIMPLE Algorithm for the closure problem in homogenization of stokes flows. Advances in Water Resources, 144, 103712.