Breadcrumb
- Home
- Publications
- Proceedings
- 2024 AIChE Annual Meeting
- Poster Sessions
- General Poster Session
- (735aj) Population Balance Modeling of the Impacts of Batch Size, Flow Rate, and Imperfect Mixing during Nanomilling of Drug Suspensions

A quantitative understanding of the impacts of process-design parameters through modeling, particularly mechanistic or first-principles-based modeling, can be highly beneficial for process development and optimization of the WSMM process [8,9]. Population balance models (PBMs) are often employed for simulation, control, and optimization of particulate processes [10,11]. In addition to describing the spatial and temporal evolution of the particle size distribution (PSD), PBMs have also been utilized to identify particle breakage mechanisms [12,13]. While several PBM studies exist for simulating batch WSMM [14] and multi-pass continuous WSMM [15], Annapragada and Adjei [16] offered the first credible PBM structure for a recirculating WSMM system. However, their model lacked thorough experimental verification and exhibited significant deviations from limited experimental data.
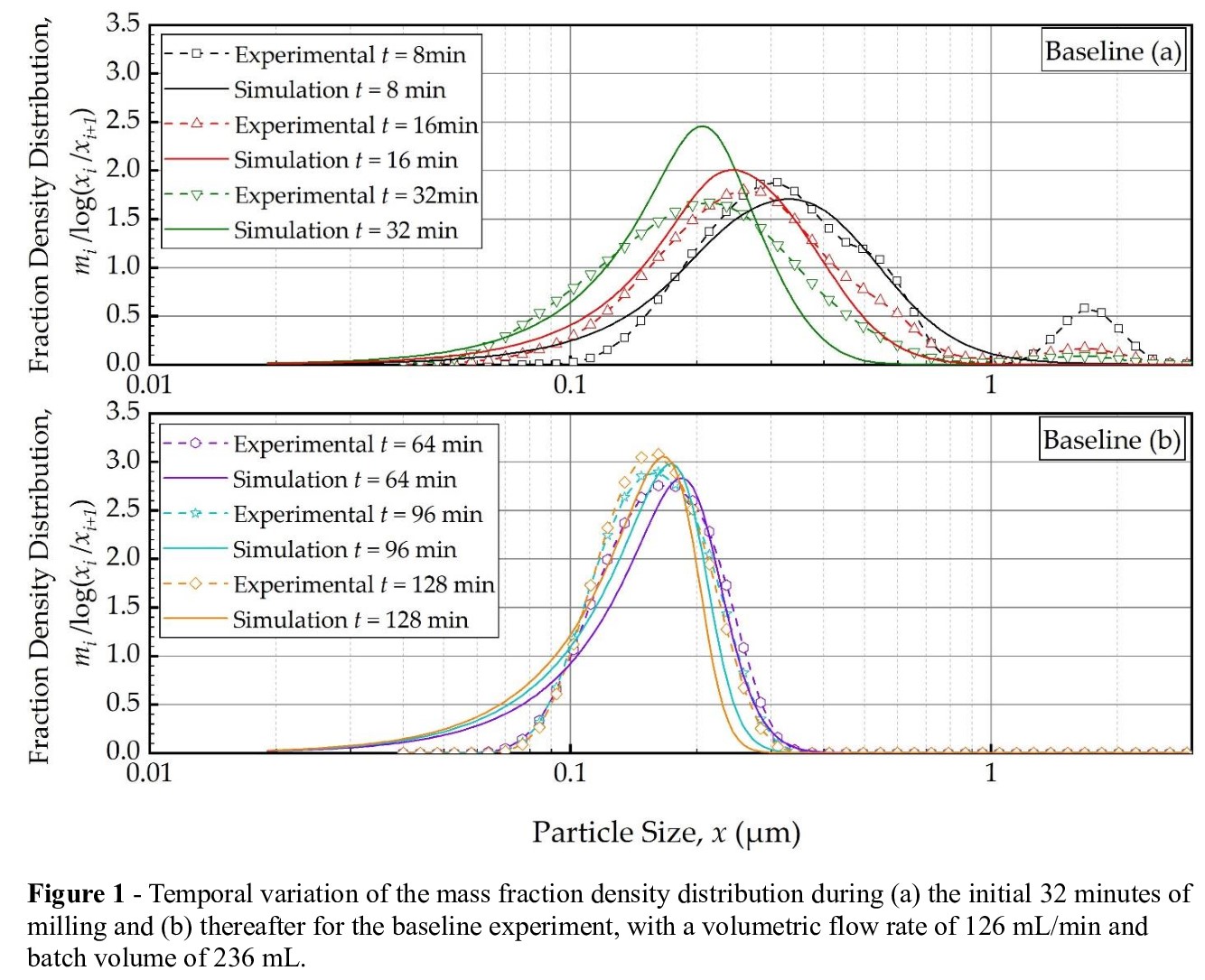
We aimed to develop and validate a cell-based PBM that allows for elucidating the impacts of batch size, suspension volumetric flow rate, and imperfect mixing within the mill chamber on the PSD evolution. Several experiments were conducted using a recirculating WSMM to produce nanosuspensions of a model poorly soluble drug, fenofibrate. Experimentally, the PSD evolution at various batch sizes (118 mL, 236 mL, and 512 mL) and suspension volumetric flow rates (63, 126, and 250 mL/min) was measured, where the baseline conditions had 236 mL batch size and 126 mL/min volumetric rate. In the first part of this study, four different specific breakage rate functions (Models A–D) were fitted to experimental PSD data at the baseline conditions, assuming a well-mixed mill. A full back-calculation method, employing a dynamic global optimizer and ODE solver, was used to estimate the breakage parameters and discriminate between the four models based on the sum-of-squared residuals (SSR). Among the four specific breakage rate functions examined, Model C, consisting of a product of power-law and logistic functions with a transition particles size, provided the best fit to the experimental PSD data at baseline conditions, with the lowest SSR. Model A (traditional power-law model) and Model B (a Heaviside unit function coupled with the power-law to capture the grinding limit) did not perform well. Figure 1 displays the PBM simulation using the best-fitting breakage rate function (Model C) alongside the experimental PSD evolution over the initial 32 min and from 64 to 128 min for the baseline condition (batch size of 236 mL and flow rate of 126 mL/min), respectively. The PBM simulations aligned well with experimental observations, capturing the shift in PSD toward finer particles and the narrowing of the distribution as milling progressed. However, the PBM struggled to accurately capture the bimodal PSD observed during the initial stages of milling, potentially arising from the presence of aggregates. This limitation highlights the need for future modeling efforts to incorporate aggregation terms in the PBM to improve its predictive capabilities. The discrimination of the four models revealed the criticality of incorporating a transition particle size commensurate with the notion of a grinding limit (Models C and D); however implausible discontinuity was observed in Model B case.
In the second part of the study, the best-fitting breakage rate function (Model C) was then used to simulate the impacts of the batch size and volumetric flow rate of the suspensions. The PBM predictions were compared with respective experimental data for model validation. Both experiments and PBM simulations demonstrated that an increase in batch size necessitates a proportionate increase in milling time to maintain the same PSD. This can be achieved by keeping the effective milling time the same for different batch sizes. The effective milling time is equal to the product of number of batch turnovers (theoretical passages through the mill) and single-pass mean residence time in the mill. The suspension volumetric flow rate was found to have an insignificant impact on the PSD evolution, as the effective milling time becomes independent of the flow rate. A key outcome of this study was the demonstration that maintaining the same effective milling time is crucial for achieving consistent product quality when scaling up or changing batch sizes. This principle was verified through simulations and experiments, where the PSDs at different batch sizes were found to be identical when the effective milling time was kept constant. These findings contradict previous simulation studies [16], which suggested a notable effect of the suspension flow rate. However, the experimental results in this study support our PBM simulations, indicating that the volumetric flow rate has a minimal influence on the PSD in a recirculating WSMM system.
In the third part of the study, the potential impact of imperfect mixing in the mill chamber was theoretically examined by considering multiple cells and different back-mixing flow ratios (R) in the cell-based PBM. The number of cells (n) and R modulate the residence time distribution (RTD) behavior, accounting for deviations from perfect mixing. An intriguing finding from the PBM simulations was that the PSD was not affected by the RTD behavior, as modulated by the n and R in the cell-based PBM, after a few turnovers in the recirculation mode.
In conclusion, this study provides valuable insights into the operation of a recirculating WSMM for nanoparticle production through the development and experimental validation of a PBM with a novel specific breakage rate function. The findings highlight the criticality of maintaining the effective milling time during scale-up or batch size changes to ensure consistent product quality. The suspension volumetric flow rate was found to have a negligible impact on the PSD evolution, contrary to previous simulation studies. Furthermore, the simulations suggest that the PSD is insensitive to the RTD behavior after a few turnovers in the recirculation mode, potentially simplifying the modeling approach by eliminating the need for detailed RTD studies. Despite some limitations, such as the inability to capture bimodal PSDs arising from aggregation during the early milling times, the newly formulated PBM offers valuable guidance for process development and scale-up of recirculating WSMM operations. Future work should focus on incorporating aggregation terms in the PBM to improve its predictive capabilities, as well as expanding the model to account for the impacts of all process parameters. Overall, this study demonstrated that a novel PBM enabled us to elucidate the impacts of the batch size, suspension volumetric flow rate, and imperfect mixing and gain fundamentals insights into the recirculating WSMM operation. It is hoped that this study will guide the batch size and scale-up studies in pharmaceutical industry.
References
1. Tanaka, Y.; Inkyo, M.; Yumoto, R.; Nagai, J.; Takano, M.; Nagata, S. Nanoparticulation of probucol using wet milling to improve bioavailability. Drug Dev. Ind. Pharm. 2012, 38, 1015-1023. [https://doi.org/10.3109/03639045.2011.640299]
2. Li, M.; Azad, M.; Davé, R.; Bilgili, E. Nanomilling of drugs for bioavailability enhancement: a holistic perspective. Pharmaceutics 2016, 8, 17. [https://doi.org/10.3390/pharmaceutics8020017]
3. Malamatari, M.; Taylor, K.M.; Malamataris, S.; Douroumis, D.; Kachrimanis, K. Pharmaceutical nanocrystals by wet milling. Drug Discov. Today 2018, 23, 534-547. [https://doi.org/10.1016/j.drudis.2017.10.021]
4. Bhakay, A.; Rahman, M.; Dave, R.N.; Bilgili, E. Bioavailability enhancement via nanocomposites: Formulation–Processing aspects. Pharmaceutics 2018, 10, 86. [https://doi.org/10.3390/pharmaceutics10030086]
5. Merisko-Liversidge, E.; Liversidge, G.G.; Cooper, E.R. Nanosizing for poorly water-soluble drugs. Eur. J. Pharm. Sci. 2003, 18, 113-120. [https://doi.org/10.1016/S0928-0987(02)00251-8]
6. Peltonen, L. QbD approach for wet media milling of nanocrystals. Pharmaceutics 2018, 10, 104. [https://doi.org/10.3390/pharmaceutics10030104]
7. Li, M.; Yaragudi, N.; Afolabi, A.; Dave, R.; Bilgili, E. Sub-100 nm drug particles by wet milling with low bead contamination. Chem. Eng. Sci. 2015, 130, 207-220. [https://doi.org/10.1016/j.ces.2015.03.009]
8. Toneva, P.; Peukert, W. Modeling of mills and milling circuits. Handbook of Powder Technology 2007, 12, 873-911. [https://doi.org/10.1016/S0167-3785(07)12020-3]
9. Bilgili, E.; Guner, G. Mechanistic modeling of wet media milling for nanosuspensions. AAPS PharmSciTech 2021, 22, 1-23. [https://doi.org/10.1208/s12249-021-01950-7]
10. Randolph, A. Theory of Particulate Processes; Elsevier: 2012.
11. Ramkrishna, D. Population Balances; Academic Press: 2000.
12. Verkoeijen, D.; Pouw, G.A.; Meesters, G.M.; Scarlett, B. Population balances: A volume approach. Chem. Eng. Sci. 2002, 57, 2287-2303. [https://doi.org/10.1016/S0009-2509(02)00115-2]
13. Hounslow, M. The population balance for particle processes. KONA Powder Part. J. 1998, 16, 179-193. [https://doi.org/10.14356/kona.1998018]
14. Bilgili, E.; Hamey, R.; Scarlett, B. Nano-milling of pigments using a wet stirred media mill. Chem. Eng. Sci. 2006, 61, 149-157. [https://doi.org/10.1016/j.ces.2004.11.069]
15. Varinot, C.; Berthiaux, H.; Dodds, J. Prediction of product size in stirred bead mills. Powder Technol. 1999, 105, 228-236. [https://doi.org/10.1016/S0032-5910(99)00142-6]
16. Annapragada, A.; Adjei, A. Numerical simulation as an aid to process design of milling. Int. J. Pharm. 1996, 136, 1-11. [https://doi.org/10.1016/0378-5173(95)04484-2]