(711e) A Q-Learning RL-MPC Algorithm Addressing Challenges Encountered in Renal Replacement Therapy

Critically ill kidney failure patients require renal replacement therapy (RRT), including hemodialysis. Intradialytic hypotension (IDH) occurs in up to 30% of RRT patients and is an independent predictor of mortality. Therefore, there is a critical need to develop a clinical decision support tool that predicts IDH and preemptively suggests therapies tailored to individual patients. Previous work [1] developed a risk-based reinforcement learning (RL) algorithm that learned personalized, dynamic treatment plans from data. However, embedding constraints and dynamic causality in RL is not straightforward. To address this, a model-driven control method like model predictive control (MPC) can be coupled with a data-driven RL approach. For systems where a fully informed mechanistic model is not feasible, like RRT, a model-driven approach can inform learning when mechanistic information is available, while still exploiting data-driven approaches when mechanistic information is limited. To this end, we construct a constrained RL-MPC algorithm that could be implemented in an RRT system to generate personalized, preemptive treatment plans for RRT patients to mitigate IDH.

Initial algorithm development was conducted using the nonlinear Van de Vusse reactor system. The degree of mechanistic model uncertainty was varied by including a subset of the known reactions within the linearized MPC model, mimicking the limited information that would be available in RRT. When the controller model is less accurate, the combined algorithm will rely upon its RL component, trained from open- and closed-loop step response data (in the Van de Vusse case), mirroring the use of sparse clinical patient record data to train the RL in an RRT setting. By using this well-characterized case study, we can test algorithmic details that leverage the benefits of RL and MPC in situations where each is most effective.

Methods

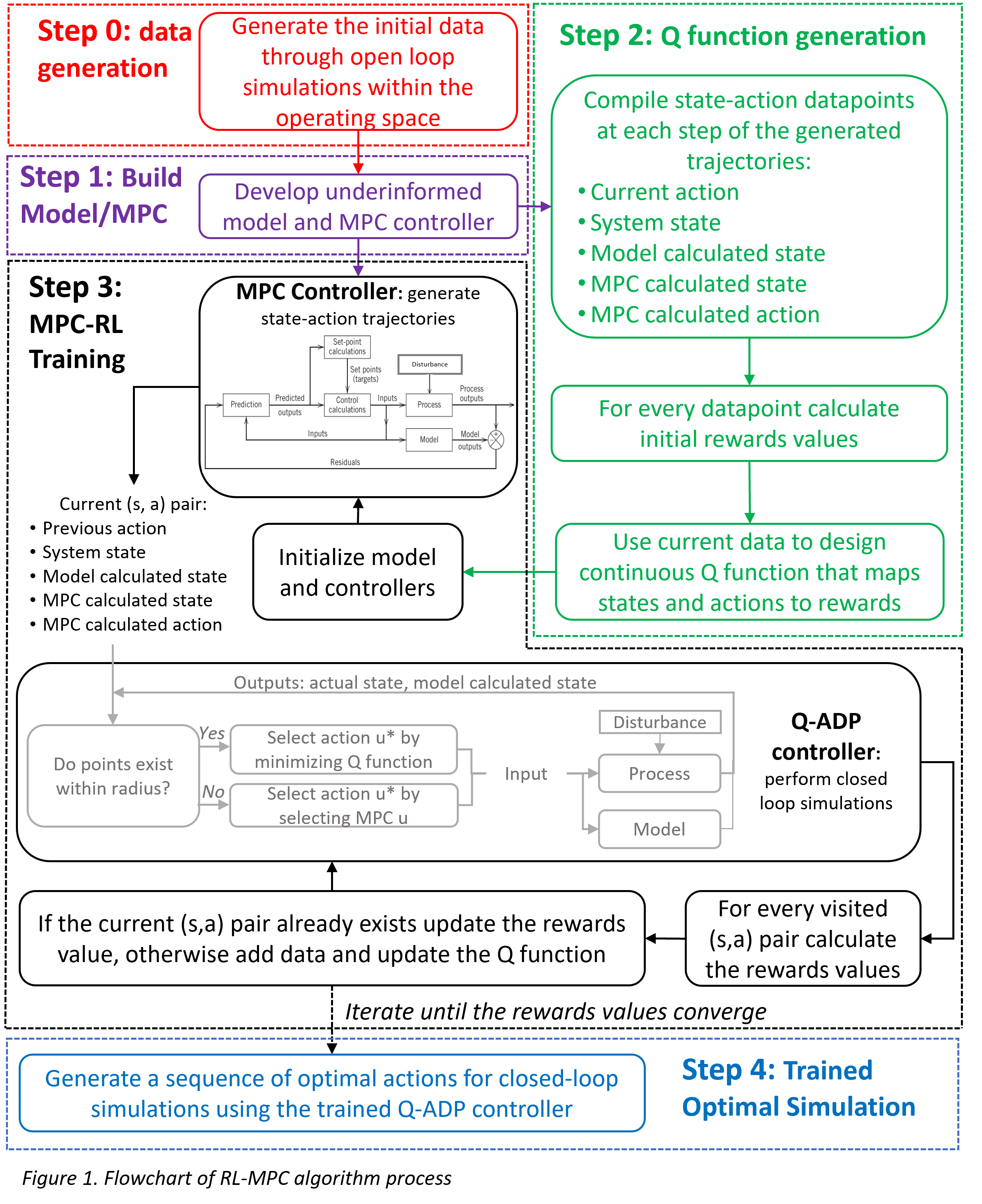
The RL-MPC algorithm was tested on the nonlinear Van de Vusse reactor system. This reaction scheme results from the production of cyclopentinol (B) from cyclopentadiene (A), with cyclopentanediol (C) and dicyclopentadiene (D) as byproducts. It was assumed that the reaction was carried out isothermally in a CSTR with a feed of pure cyclopentadiene (C_A,feed=10 mol*L^-1) and set reaction rate constants (k_AB=5/6 min^-1, k_BC=5/3 min^-1, k_AD=1/6 L*mol^-1*min^-1). The goal of the controller was to drive the concentration of cyclopentinol, C_B, to a target concentration by adjusting the dilution rate, F/V. An underinformed linear model that did not include the formation of the byproduct dicyclopentadiene was developed to mimic the limited mechanistic information available in the RRT system. This model was used within the MPC controller that generated state and action trajectories (Figure 1, Step 1). The states that were incorporated in the RL continuous state space included measured C_B(k), the underinformed linear model-calculated C_B,model(k), the current-time MPC predicted C_B(k), and the MPC generated current-time action. This state space allowed the RL to map system-model mismatch and MPC trajectories to rewards, which is useful in systems with limited mechanistic information (like RRT). A rewards function was designed so that state-action pairs that drove the system C_B closer to the target concentration had higher value.

The states and actions were mapped to rewards values using a Q-learning approximate dynamic programming (Q-ADP) approach. Unlike traditional Q-learning algorithms, a Q-ADP algorithm allowed for continuous states and actions by utilizing a function approximator to map states-actions to rewards in a Q function. A simple radius nearest neighbors function approximator was developed to serve as the Q function (Figure 1, Step 2); this was favored over a k nearest neighbors function approximator to mitigate concerns associated with extrapolation due to the effect of any outlier points.

Finally, the Q-ADP controller was trained through closed-loop simulations where rewards were used as intermittent feedback to learn a sequence of optimal actions (Figure 1, Step 3). Closed-loop trajectories were generated by minimizing the current Q function to produce the optimal action at each visited state. Data were added and rewards values were updated based on the results of these trajectories. The Q function was retuned as closed-loop simulations added data. Disturbances to the feed concentration were added during training to increase the size of operating space that was explored. During simulations, if no current-time data points existed within the radius of the Q function and therefore the Q function could not be trusted, exploration was necessary because the Q-ADP controller was encountering a new state-action space. To address this, the MPC generated action at that timepoint was implemented to allow the Q-ADP controller to safely explore new states and actions. Thus, the RL-MPC algorithm would trade-off to move towards MPC-driven control when the RL could not be trusted. As the Q-ADP controller learned from this exploration, the Q function was updated to incorporate an expanded operating range that included disturbances. As a result, the RL-MPC algorithm relied less on MPC-driven control as data were added because the Q function could be trusted in this expanded operating range. Therefore, MPC was utilized further to inform RL. This process was repeated until rewards values converged. The L1 norm of rewards values over training iterations was recorded to track convergence. After training, the RL-MPC algorithm was tested in closed-loop for various disturbance cases (Figure 1, Step 4).

Results

Initial data for the Van de Vusse reactor system were generated by simulating open-loop responses to step changes in the dilution rate (F/V_init∈[0.4,0.7 min^-1]) to produce 3147 initial data points (C_Binit∈[0.56,1.25 mol*L^-1]). The initial data were unevenly distributed across the state-action space to mimic sparse RRT data conditions. The target concentration was C_B=1.12 mol*L^-1. A MPC controller was aggressively tuned (M=2, P=10, sample time=12 sec) and used to further inform the Q-ADP controller during training. The radius nearest neighbors function approximator was tuned with 100-fold cross validation to minimize the difference between predicted and calculated rewards values (initial radius = 0.215). During training, for simplicity in testing the algorithm, closed-loop simulations were initialized at one test steady state (F/V=0.5 min^-1, C_B=1.08 mol*L^-1). Disturbances to the feed concentration of ±10% were added during training to expand the tested operating space.

The L1 norm of rewards values showed that the Q-ADP algorithm converged in 35 training iterations with 2241 data points added during training. The radius nearest neighbors function approximator was retuned throughout training to account for these additional points (final radius = 0.157). Comparison of pre-training and post-training simulations showed that the RL-MPC algorithm learned from both the data and the MPC generated trajectories to produce a sequence of optimal actions. For simulations without an added disturbance to feed concentration, the rewards value improved by 14.5%, and the mean absolute error (MAE) between system and target C_B improved by 6%. Additionally, MPC allowed the Q-ADP algorithm to explore new states and update the Q function to more accurately approximate the state-action space. In simulation, the RL-MPC algorithm drove the system towards MPC-driven control when sparse RL data meant that the RL could not be trusted. Prior to training, the Q function incorporated a limited operating range, so MPC-driven control was necessary in simulations where a disturbance drove the state space outside of this initial range. After training, the Q-ADP controller learned from MPC-driven exploration, and the updated Q function accounted for an expanded operating range that included disturbances to the feed concentration. As a result, post-training simulations relied less on MPC-driven control because the Q function could be trusted in the expanded operating range. In simulations with a +10% feed concentration disturbance, the percentage of actions selected by minimizing the Q function rather than implementing the MPC generated action increased from 13% to 100% post-training. Furthermore, the rewards value improved by 27% and the MAE improved by 12%. Simulations where the disturbance in feed concentration was turned on and then off showed that the trained Q-ADP controller could drive the states and action back towards the target after a perturbation. Therefore, by utilizing MPC trajectories, the MPC-RL algorithm learned an expanded state-action space until a pure RL-driven approach could be implemented for control of the tested operating range.

Summary and Significance

Previous Q-ADP and RL-MPC studies have focused on using RL to improve the primary MPC controller, usually through integrating RL within MPC model optimization or the MPC cost function. In contrast, this work uses information generated by MPC trajectories to further inform the primary RL controller. This RL-MPC algorithm exploits both data-driven Q-ADP and model-driven MPC to control a system with continuous states and actions under incomplete mechanistic information. We tested the RL-MPC algorithm on the Van de Vusse system, which has characteristics analogous to the clinical RRT optimization problem. The results demonstrate the advantage of MPC-driven exploration when RL data is sparse, as well as the superior performance achievable once the RL can update using the MPC actions and system responses. This RL-MPC algorithm shows promise for application in RRT where mechanistic processes that are well-characterized, like patient fluid volume, could be modeled explicitly, while data-driven approaches capture system-level observations of unmeasurable intra-organ and intracellular processes that are not as well understood.

[1] McLaverty, et al. [Paper presentation]. FOCAPO, 2023.