(458d) A Model-Free Approach to Nonlinear State Observation from Video Data

In nonlinear process control, state-space representations serve as the standard framework, facilitating the synthesis of optimal state-feedback controllers [5]. However, before implementing such controllers, the design of a state observer is imperative to estimate the states from historical input and output data. A state observer refers to an auxiliary dynamical system that estimates states from input and output measurements [6]. Traditional solutions like the Luenberger observer [7] fall short in handling nonlinear systems, leading to the exploration of innovative alternatives such as extended Kalman filters, input-output linearization, high-gain observers, and other ideas [8]. This study focuses on the Kazantzis-Kravaris/Luenberger (KKL) observer [9], which provides a systematic solution for synthesizing nonlinear state observers [10]. Various extensions of KKL observers have been proposed in the literature [11].

Notably, the KKL observer exhibits a distinctive structure comprising linear state dynamics and a nonlinear static output map. This structure lends itself well to machine learning techniques, particularly neural network approaches. To circumvent nonconvexity issues encountered in neural network training, a recent innovation introduces a linear parameterization of the observer in the form of the Chen-Fliess series [12]. This parameterization can be recursively learned through online least squares, enhancing computational efficiency and facilitating real-time application.

In this paper, we investigate scenarios where high-dimensional visual measurements are available from an (autonomous) system characterized by a low-dimensional state space. Despite the inherent potential of utilizing such rich visual information for state observation [13], which in principle provides a higher capacity for understanding and handling the nonlinear process dynamics [14], its application, however, has not been previously explored to the best of our knowledge. Our study aims to address this gap, particularly focusing on reactive systems exhibiting significant nonlinearity. We present a streamlined methodology for the data-driven synthesis of KKL observers, aimed at simplifying observer design without compromising accuracy.

• First, output measurements are transformed using pre-assigned linear time-invariant dynamics to compute observer states in a KKL observer. The resulting observer states that contain state information is high-dimensional.
• Thus, we approximate the observer's output mapping as affine and employ principal component analysis (PCA) for dimensionality reduction, producing a low-dimensional state trajectory that captures the system dynamics.

This method establishes a topological equivalence between the estimated and actual state trajectories, facilitating subsequent state-space modeling and potentially enabling model-free state-feedback control.

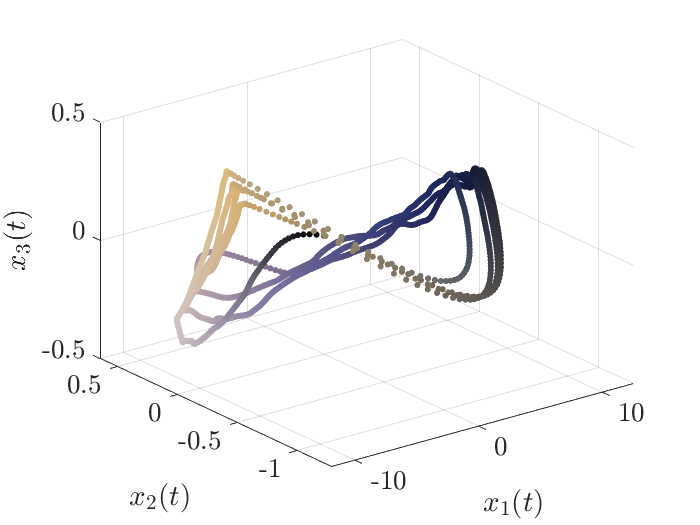
As a demonstration of the methodology's applicability, we present a case study on the Belousov-Zhabotinsky (B-Z) reaction system, a prototypical example of a nonlinear autonomous system. The B-Z reaction system [15] showcases repetitive oscillations across a spectrum of colors attributed to periodic variations in the concentrations of reactive species. The proposed method synthesizes a KKL observer which was able to construct states that have similar trajectories and topological correspondence to the Oreganetor model [16] which describes the B-Z reaction. The KKL observer also catches decays in the limit cycle which is representative of a real system but is not captured by the model.

References:

[1] Rawlings, J.B., Mayne, D.Q., and Diehl, M. (2017). Model predictive control: Theory, computation, and design. Nob Hill, 2nd edition.

[2] Nelles, O. (2020). Nonlinear dynamic system identification. Springer, 2nd edition.

[3] Ren, Y.M., Alhajeri, M.S., Luo, J., Chen, S., Abdullah, F., Wu, Z., and Christofides, P.D. (2022). A tutorial review of neural network modeling approaches for model predictive control. Comput. Chem. Eng., 107956.

[4] Tang, W. and Daoutidis, P. (2022). Data-driven control: Overview and perspectives. In 2022 American Control Conference (ACC), 1048–1064. IEEE.

[5] Sontag, E.D. (1998). Mathematical control theory: Deterministic finite dimensional systems. Springer, 2nd edition.

[6] Kravaris, C., Hahn, J., and Chu, Y. (2013). Advances and selected recent developments in state and parameter estimation. Comput. Chem. Eng., 51, 111–123.

[7] Luenberger, D. (1966). Observers for multivariable systems. IEEE Trans. Autom. Control, 11(2), 190–197.

[8] Bernard, P., Andrieu, V., and Astolfi, D. (2022). Observer design for continuous-time dynamical systems. Ann. Rev. Control, 53, 224–248.

[9] Kazantzis, N. and Kravaris, C. (1998). Nonlinear observer design using Lyapunov’s auxiliary theorem. Syst. Control Lett., 34(5), 241–247.

[10] Andrieu, V. and Praly, L. (2006). On the existence of a Kazantzis-Kravaris/Luenberger observer. SIAM J. Control Optim., 45(2), 432–456.

[11] Duan, Z. and Kravaris, C. (2020). Nonlinear observer design for two-time-scale systems. AIChE J., 66(6), e16956.

[12] Tang, W. (2023). Data-driven state observation for nonlinear systems based on online learning. AIChE J., 69(12), e18224.

[13] Shi, J., Chang, Y., Xu, C., Khan, F., Chen, G., and Li, C. (2020). Real-time leak detection using an infrared camera and faster R-CNN technique. Comput. Chem. Eng., 135, 106780.

[14] Chiang, L.H., Braun, B., Wang, Z., and Castillo, I. (2022). Towards artificial intelligence at scale in the chemical industry. AIChE J., 68(6), e17644.

[15] Zhabotinsky, A.M. (1991). A history of chemical oscillations and waves. Chaos, 1(4), 379–386.

[16] Field, R.J., Mazo, R.M., and Manz, N. (2022). Science, serendipity, coincidence, and the Oregonator at the University of Oregon, 1969–1974. Chaos, 32(5), 052101.