(364b) Simplest Mechanism Builder Algorithm (SIMBA)

Research Interests: automated knowledge discovery, machine learning, reaction engineering

Introduction

Understanding reaction mechanisms is essential for developing microkinetic models, vital in sectors like business and public policy. In business, they help engineers assess the profitability of chemical plants. In policymaking, they may support environmental treaties like the Stockholm Convention by understanding chemical degradation in the environment. Achieving a balance between model accuracy and simplicity is crucial for computational efficiency and interpretability.

Traditionally, experts manually constructed these models, identifying possible reaction steps and intermediates. This manual process, potentially covering hundreds of thousands of interactions, is slow, prone to errors, and highly complex. The uptake of data-driven methods and improved analytics has popularized automated mechanism development. These are categorized into combinatorial algorithms and characteristic reaction generators based on known reaction classes. The former often yields overly complex mechanisms that hinder computational efficiency and interpretability. The latter relies on existing reaction class knowledge, which may not be available. For in-depth discussions on these methodologies, reviews by van de Vijver et al. [1] and Ratkiewicz and Truong [2] are recommended.

These challenges have led to the development of SIMBA (SImplest Mechanism Builder Algorithm), a new methodology aiming to construct minimal reaction networks accurately reflecting kinetic data without prior system knowledge.

Methodology

SIMBA (SImplest Mechanism Builder Algorithm) aims to generate microkinetic models from kinetic data, seeking the simplest yet accurate reaction mechanism. It involves four main phases: the reaction chain generation phase, the ODE system builder phase, the system integration phase, and the comparison phase. Each phase is designed to streamline the process of developing a minimalistic yet precise kinetic system model. The following subsections will provide a closer look at these phases.

Reaction Chain Generation

Our methodology's initial phase systematically proposes reaction mechanisms, starting with the simplest and incrementally increasing in complexity. This process is grounded on assumptions such as knowing the overall reaction stoichiometry and the exclusion of termolecular or higher-order interactions, considered physically improbable. These assumptions help estimate the minimal number of elementary steps and intermediates needed for the simplest mechanism.

We represent reaction mechanisms using matrix notation, where each row corresponds to an elementary reaction step and each column to a chemical species (reactant, product, or intermediate). In this framework, negative values indicate the consumption of a species, and positive values represent production, with interaction magnitudes ranging from i ∈ [-2, 2].

Feasibility of the matrix is determined by rules: reactions must be bi- or unimolecular, summing elementary steps must add to the overall stoichiometry, and intermediates must form before they are consumed. The combinatorial complexity of constructing these matrices – where a small 3 by 5 matrix yields over 30 billion combinations – renders exhaustive search methods infeasible. This challenge is similar to Sudoku. In Sudoku, a backtracking algorithm is used to efficiently explore the solution space by building potential solutions incrementally and backtracking when encountering dead ends.

Implementing backtracking allows us to reduce the search space, enabling a thorough but manageable examination of all plausible reaction mechanism arrangements. This systematic exploration sets the stage for subsequent phases, where reaction mechanisms are iteratively refined. Through this process, SIMBA aims to distill the kinetic behavior of the system into its simplest, most accurate representation, laying a solid foundation for further model improvement.

ODE System Builder

Following the initial phase, SIMBA advances to the next stage: the transformation of these theoretical mechanisms into microkinetic models, each represented by a system of ODEs. This automatic formulation is critical for translating theoretical reaction mechanisms into quantifiable models that we can then optimize and evaluate computationally.

System Integration

In this phase, SIMBA utilizes the L-BFGS-B algorithm to estimate kinetic parameters, crucial for the model's accuracy in reflecting the system's kinetics. The parameter estimation step optimizes parameters to minimize the discrepancy between predicted and measured concentrations of species across n_t experimental data points. Here, the objective function is the sum of squared errors between the predicted and actual concentrations at time t⁽ⁱ⁾. By minimizing these errors, the model is fine-tuned to closely match experimental observations, enabling model evaluation and comparison.

Model Comparison

In SIMBA's final stage, the developed microkinetic models, each with optimized kinetic parameters, undergo a comparison to determine whether further iterations are required. This analysis uses the Akaike Information Criterion (AIC) to assess model performance. The AIC can be found in the work of Akaike [3]. A lower AIC indicates a better model that balances high model accuracy with low complexity. This criterion, proven effective for kinetic modeling [4], avoids overfitting by penalizing complexity. SIMBA's decision to proceed or conclude hinges on whether the best model in iteration n yields a lower AIC compared to the best model in iteration n - 1. This process guarantees that SIMBA explores a broad spectrum of mechanisms, converging on a simple yet accurate model that captures the system's kinetics.

Case Study

The case study used for the performance analysis of SIMBA is the dehydration of fructose to 5-hydroxymethylfurfural (HMF), catalyzed by [BmimHSO₃][HSO₄]. Based on Hu et al. [5], we developed a microkinetic model following a proposed mechanism with three dehydration steps involving three intermediates (Int₁, Int₂, Int₃) through the conversion process from fructose (A) to HMF (C), with water (B) as a by-product.

To generate the in-silico data set, we simulated three computational studies with the following initial conditions (in molar units): (C_A(t = 0), C_B(t = 0), C_C(t = 0)) ∈ {(4, 0, 0), (6, 2, 1), (4, 2, 0)}. For each experiment, the concentration of the reactant and products are recorded 30 times, at evenly spaced intervals between time t₀ = 0 h and t_f = 2 h. The kinetic parameters were defined as: k₁ = 1.514 h^-1, k₂ = 5.259 h^-1, k₃ = 9.352 h^-1 and k₄ = 2.359 h^-1.

Gaussian noise is added to the in-silico measurements to simulate a realistic chemical system. The added noise had zero mean and a standard deviation of 0.2 for all observed species.

Results and Discussion

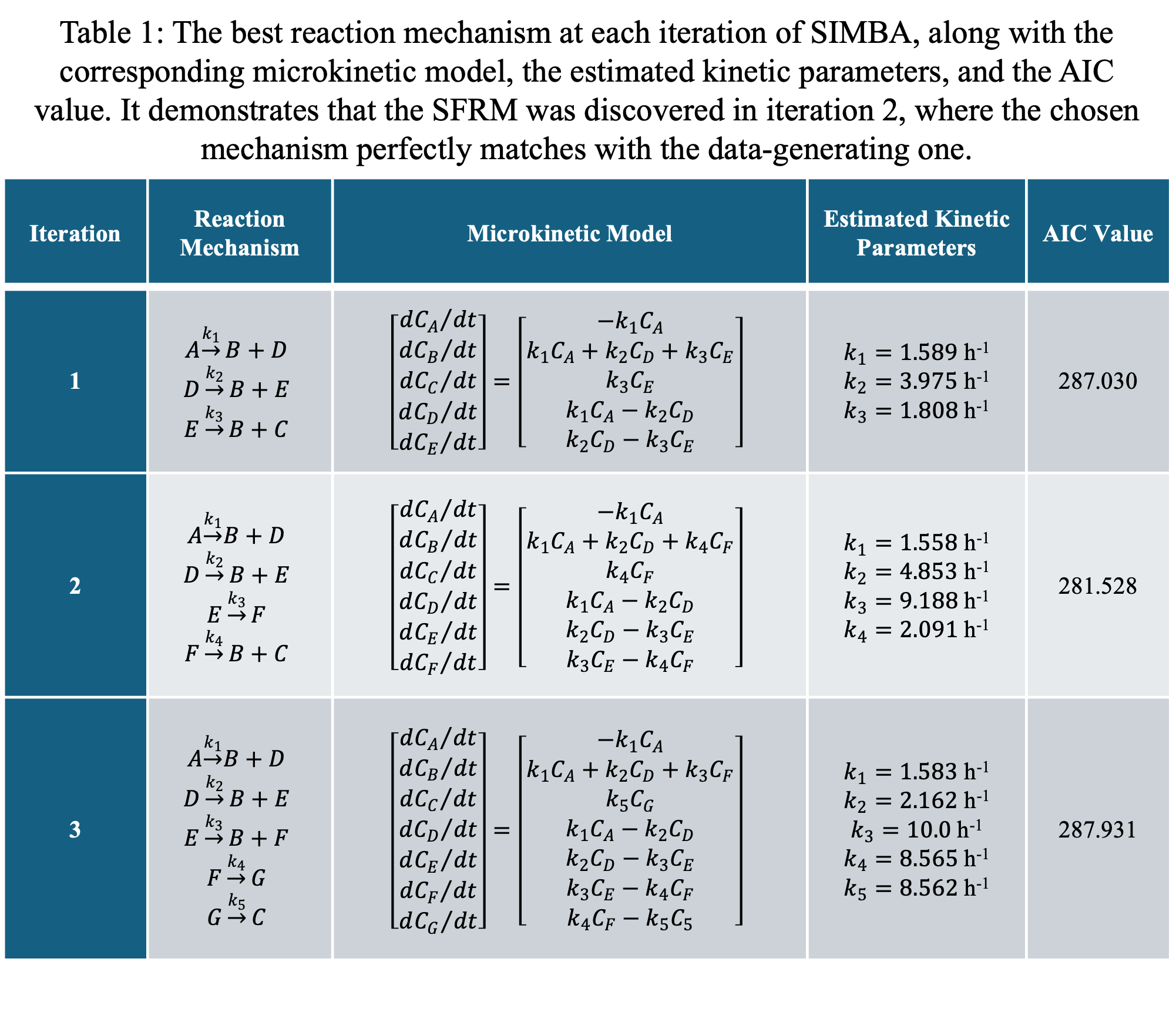
SIMBA's application to in-silico data successfully identified the smallest feasible reaction mechanism (SFRM) within just three iterations, pinpointing the optimal SFRM in the second iteration as demonstrated by the AIC values. Table 1 (see attachment) summarizes the microkinetic models, their estimated kinetic parameters, and AIC values for each iteration's best mechanism, offering a clear and concise overview.

The case study showcased SIMBA's capacity to unveil the governing microkinetic model, despite assumptions like the rarity of ter- and higher-order interactions. This demonstrates SIMBA’s promise as a tool for kinetic discovery. However, SIMBA's approach to proposing mechanisms, although it successfully predicts intermediates, lacks the capability to chemically identify these intermediates. For simpler systems, basic chemical knowledge may suffice to deduce intermediates, but more complex systems could challenge this approach, underlining the need for expert intervention.

Despite these limitations, SIMBA stands out as a tool for chemists and reaction engineers, complementing rather than replacing expert insight. It streamlines mechanistic exploration, offering a strong initial mechanism ‘guess’ that facilitates the rapid design and optimization of chemical processes, highlighting its value in accelerating the understanding and development of complex chemical systems.

Conclusions

The algorithm SIMBA is presented in this study. It consists of four stages: reaction chain generation, ODE builder, system integration, and model comparison. When tested with the catalyzed synthesis of HMF from fructose, SIMBA successfully identified the SFRM from in-silico data, matching the literature-sourced microkinetic model. This demonstrates that even with the drawback of not being able to chemically identify reaction intermediates, SIMBA has the potential to speed up mechanistic discovery.

Future research will focus on integrating uncertainty quantification in model predictions and integrating more chemical knowledge into SIMBA, which is essential for assisting in the identification of complex systems. By implementing these improvements, SIMBA will become a more powerful tool for chemists and reaction engineers, both in terms of efficiency and reliability when it comes to finding and refining microkinetic models.

References

[1] R. van de Vijver, N. M. Vandewiele, P. L. Bhoorasingh, B. L. Slakman, F. S. Khanshan, H.-H. Carstensen, M.-F. Reyniers, G. B. Marin, R. H. West, K. M. van Geem, 2014, Automatic Mechanism and Kinetic Model Generation for Gas- and Solution-Phase Processes: A Perspective on Best Practices, Recent Advances, and Future Challenges, International Journal of Chemical Kinetics, 47, 4, 199-231

[2] A. Ratkiewicz, T. N. Truong, 2005, Automated Mechanism Generation: From Symbolic Calculation to Complex Chemistry, International Journal of Quantum Chemistry, 106, 1, 244-255

[3] Akaike H. A New Look at the Statistical Model Identification. In: Springer Series in Statistics. Springer New York; 1974. p. 215-22. 7

[4] M. Á. de Carvalho Servia, I. O. Sandoval, K. K. Hii, K. Hellgardt, D. Zhang, E. A. del Rio Chanona, 2023, The Automtaed Discovery of Kinetic Rate Models – Methodological Frameworks, arXiv

[5] J. Hu, M. Yu, Y. Li, X. Shen, S. Cheng, T. Xu, C. Ge, Y. Yu, Z. Ju, 2023, Dehydration mechanim of fructose to 5-hydroxymethylfurfural catalyzed by functionalized ionic liquids: a density functional theory study, New Journal of Chemistry, 47, 11525-11532.