(279a) Dynamics of Molecular Collisions in Air and Its Mean Free Path

The kinetic theory of gases (Maxwell, 1860; Jeans, 1967) offers a remarkable description of molecular collisions in gases with its hard-sphere model and under the assumption of collisions being purely elastic. In practical applications, however, such as in the aerosol synthesis of small nanoparticles at high temperatures and/or low pressures, one must accurately account for gas-particle collisions as asymptotic (self-preserving) particle size distributions and (fractal-like) structure have not been attained to simplify aerosol dynamics (Pratsinis, 2010). Then, the classic hard-sphere model might be insufficient to describe them. Motivated by such a need, we compare the kinetic theory with detailed molecular dynamics (MD) simulations for the dynamics of molecular collisions in air accounting, however, for oxygen and nitrogen as diatomic molecules, for the first time to the best of our knowledge.

The MD simulations were conducted in the NVE ensemble using simulation cells containing 21% mole O₂ and 79% mole N₂ with a fully atomistic (FA) model (Zambrano et al., 2014). The simulations were carried out at 300 K and 1 atm to validate our methodology with textbook results for density and transport properties. A distance criterion was set to identify collisions based on the separation between colliding molecules, as in kinetic theory. The force field employed was validated by comparing the MD-predicted air density (1.18 kg/m³) to the experimental for dry air (1.18 kg/m³). A second validation test involved a comparison of the MD-predicted values for the diffusion coefficient and viscosity with available measured values. Again, a good agreement was found.

Treating O₂ and N₂ as hard spheres, their collision densities by the MD simulations were also in agreement with their densities from kinetic theory (Jeans, 1967). When, however, these densities were calculated with the FA model, they were distinctly above those of the kinetic theory. This is attributed to the attractive part of the Lennard-Jones (LJ) interactions and their diatomic, thus more voluminous, shape. To this, simulations were repeated with O₂ and N₂ considered as LJ spheres. Their collision densities fell between those from the kinetic theory and the FA model.

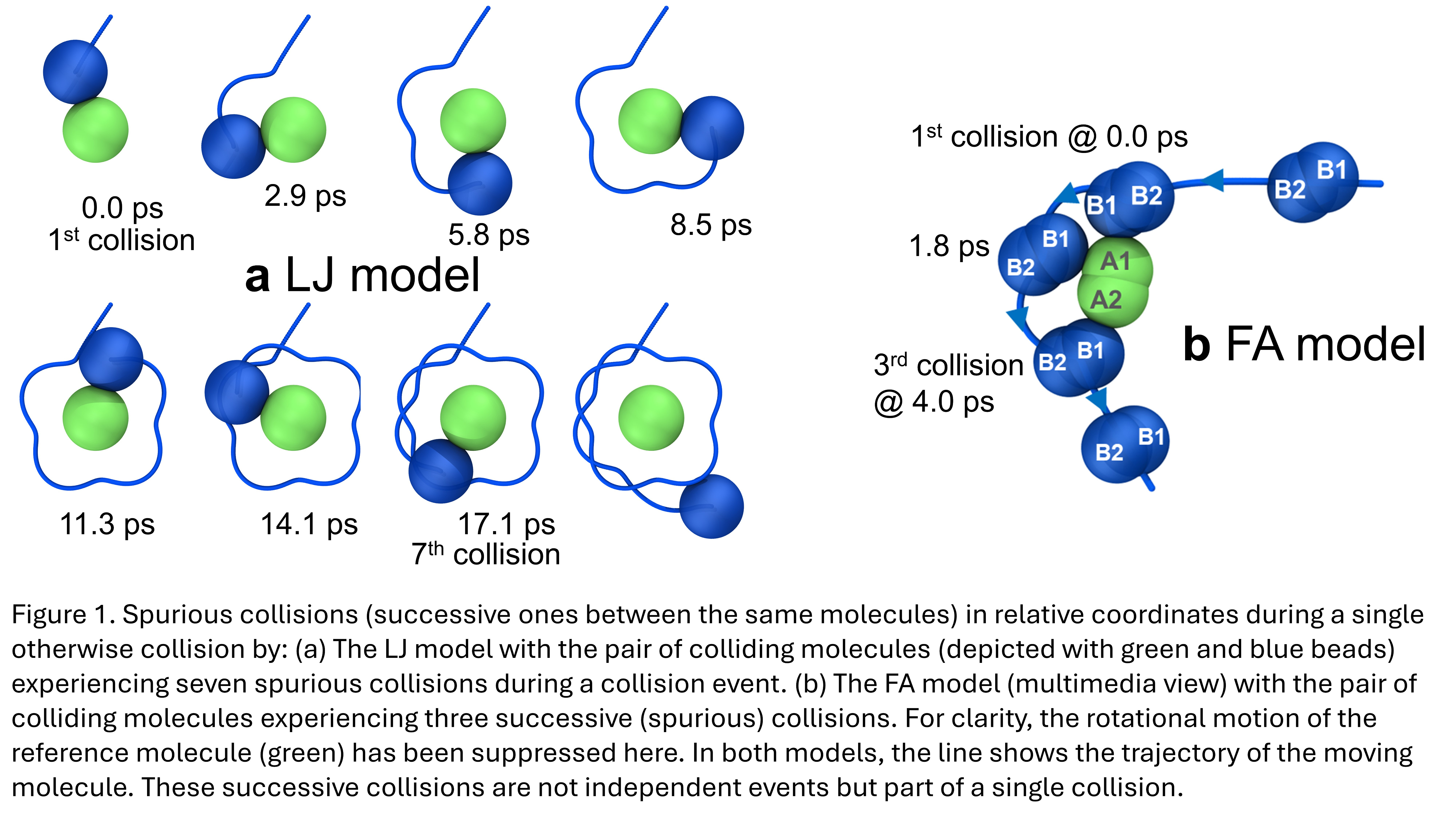
A detailed analysis of the extracted MD trajectories revealed that molecular collisions by the FA model involve strong interactions of the colliding species. There were instances where three or four molecules were involved in the same collision. Moreover, frequently, colliding molecules split from each other but soon returned to collide again and again without having interacted with any other molecule in between. Such collisions are termed spurious. Systematically, spurious collisions were identified and removed in the analysis to avoid overcounting collision events. These complex collision patterns were detected by the LJ model (Figure 1a) and the FA model (Figure 1b), but they were never observed by the HS model.

A direct result of the enhanced interactions between air molecules when these are treated as diatomic molecules is that their mean free path (MFP) (calculated both by the collision densities and by direct averaging over the probability distribution of free paths) comes out to be considerably smaller than that from the classic HS potential. The new value of the MFP of air, λ, reported here from our all-atom MD simulations is 38.5 ± 1 nm (Tsalikis et al., 2023), almost 43% smaller than the currently known and widely used value of 67.3 nm at 300 K and 1 atm (Jennings, 1998). The MD-extracted λ, is quite robust to the employed MD force field as long as it accurately matches the experimentally determined macroscopic properties of air (density, viscosity, and diffusivity).

References

J. Jeans, An introduction to the kinetic theory of gases, (Cambridge University Press, Cambridge, 1967).

S.G. Jennings, The mean free path in air, J. Aerosol Sci. 19 (1998) 159-166, doi.org/ 10.1016/0021-8502(88)90219-4.

J.C. Maxwell, Illustrations of the dynamical theory of gases-part I. On the motions and collisions of perfectly elastic spheres, The London, Edinburgh, and Dublin Philos. Mag. and J. of Science 19 (1860) 19-32, doi.org/ 10.1080/14786446008642818.

S.E. Pratsinis, Aerosol-based technologies in nanoscale manufacturing: From functional materials to devices through core chemical engineering, AIChE J. 56 (2010) 3028-3035, doi.org/ 10.1002/aic.12478.

D.G. Tsalikis, V.G. Mavrantzas, S.E. Pratsinis, Dynamics of molecular collisions in air and its mean free path, Phys. Fluids. 35, (2023) 097131, doi.org/10.1063/5.0166283.

H. Zambrano, J.H. Walther, R. Jaffe, Molecular dynamics simulations of water on a hydrophilic silica surface at high air pressures. J. Mol. Liq. 198 (2014) 107-113, doi.org/ 10.1016/j.molliq.2014.06.003.